Überblick

Nach Winter (1996) gibt es drei Grunderfahrungen, die ein allgemeinbildender Mathematikunterricht ermöglichen muss. Eine der drei Grunderfahrungen ist es, in der Auseinandersetzung mit Aufgaben Problemlösefähigkeiten (bzw. heuristische Fähigkeiten), die über die Mathematik hinausgehen, zu erwerben. Was heuristische Fähigkeiten sind und wie man die Problemlösekompetenz im Unterricht fördert sind Fragen, denen wir uns in diesem Modul zuwenden möchten.

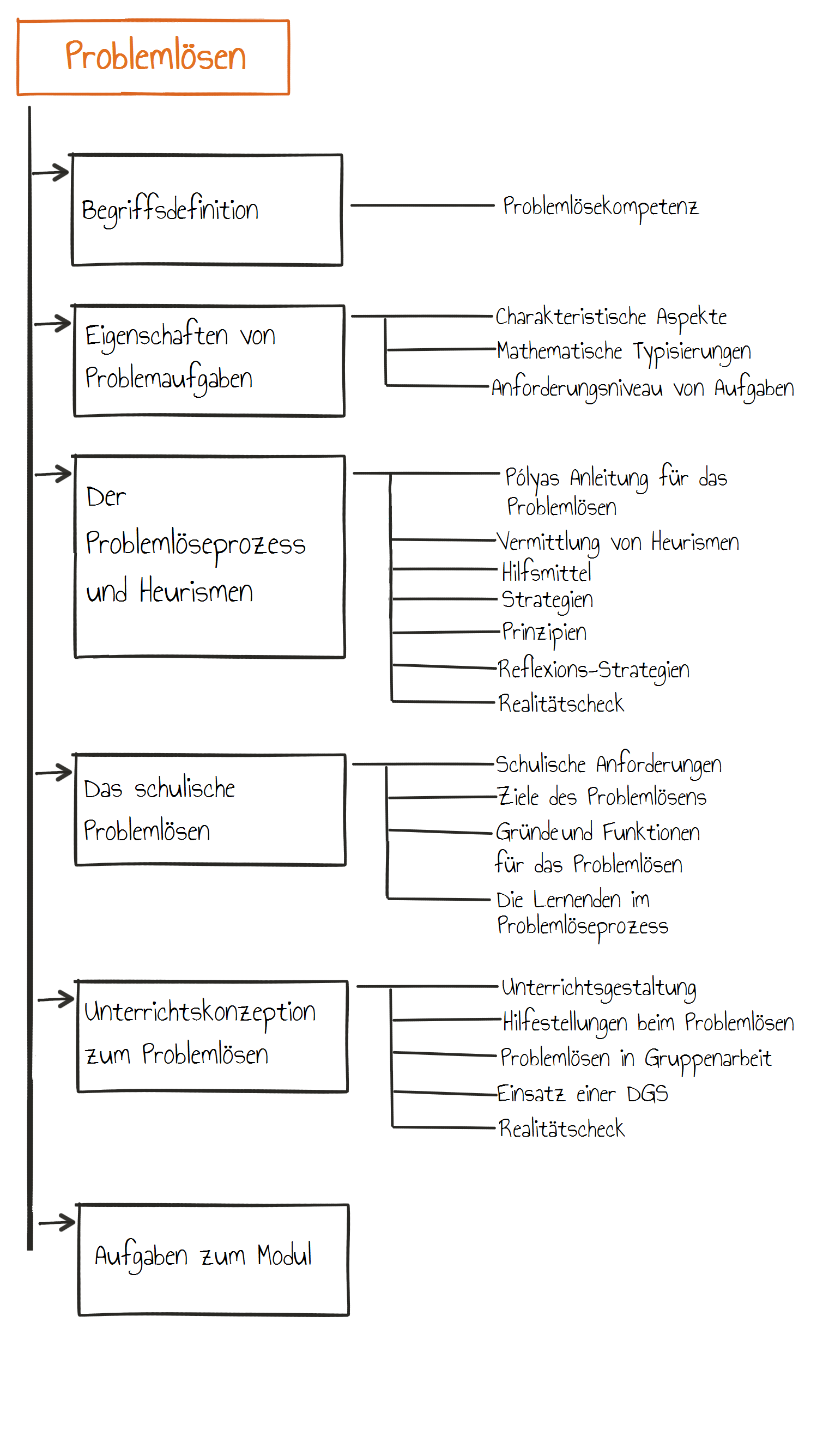
Zu Anfang werden einige Grundlagen eingeführt, die im Folgenden immer wieder eine Rolle spielen. Zunächst werden die Begriffe „Problem“ und „Aufgabe“ voneinander abgegrenzt, um herauszufinden, welcher spezielle Typ von Problemaufgaben in diesem Modul genauer betrachtet wird. Danach wird der theoretische Hintergrund der Problemlösekompetenz erläutert.

Danach werden charakteristische Aspekte von Problemaufgaben betrachtet und deren spezielle Unterteilung in mathematische Probleme erläutert. Im Anschluss daran folgen Überlegungen, wann eine Aufgabe eigentlich schwierig ist und welche Faktoren dabei eine Rolle spielen. Der Ablauf des Problemlöseprozesses folgt der Anleitung zum Problemlösen von Pólya (1995).

Bevor das schulische Problemlösen behandelt wird, folgt eine Einführung in die Heurismen. Es werden die Fragen geklärt, was Heurismen sind, wie ihre Verwendung im Unterricht geübt werden kann, mit welchen Reflexionsstrategien die Lernenden die Heurismen noch besser einsetzen können und ob heuristische Fähigkeiten im Unterrichtsalltag tatsächlich das Problemlösen der Lernenden verbessern. Beim schulischen Problemlösen geht es um die Anforderungen, die eine Problemaufgabe im Unterricht erfüllen muss, um sinnvoll genutzt werden zu können, und um die Ziele, Gründe und Funktionen dieser Aufgaben. Im Anschluss richtet sich der Fokus wieder auf die Lernenden und es wird erörtert, welche Fähigkeiten die Lernenden für den Problemlöseprozess benötigen.

Anschließend wird gezeigt, wie die Unterrichtsgestaltung im Sinne des problemlösenden Unterrichts geschehen kann und welche Voraussetzungen dies für die Lernenden impliziert. Es wird aufgezeigt, mit welchen Hilfestellungen Lehrende den Problemlöseprozess der Lernenden unterstützen können und warum sich die Gruppenarbeit für solche kreativen und offenen Aufgaben eignet. Kurz wird auch der Einsatz einer dynamischen Geometriesoftware im Unterricht angesprochen. Dabei werden Vor- und Nachteile des Medieneinsatzes beleuchtet. Zum Schluß wird das Problemlösen ganz generell im Unterrichtsalltag betrachtet.

Zum Ende besteht die Möglichkeit, das neu gelernte Wissen mit Hilfe verschiedener Aufgabenformate zu überprüfen. In den Aufgaben für das Selbststudium können Sie Ihr erworbenes Wissen zu den Inhalten der Lernmaterialien testen und unter Aufgaben für die Seminareinheit ausgewählte Fragestellungen zum Thema gemeinsam diskutieren.

Ab und an finden Sie auf den Theorieseiten auch Impulsfragen, die Sie zum Reflektieren über das Gelesene anregen. Diese können Sie für sich beantworten oder mit einem Lernpartner oder in einer Lerngruppe besprechen.

Die dazugehörigen Referenzen können Sie im Kapitel Literatur einsehen.