Fachdidaktik Mathematik: Problemlösen
Aufgaben I-V
Aufgabe I
Wählen Sie eine zufällige Aufgabe aus einem Schulbuch. Versuchen Sie sie in dieses Schema einzuordnen. Was ist der Zweck dieser Aufgabe? Erkennen Sie ein Muster in allen Aufgaben auf Ihrer Schulbuchseite?
Diskutieren Sie Ihre Ergebnisse im Kurs oder vergleichen Sie sich mit der Lösung.
Aufgabe II
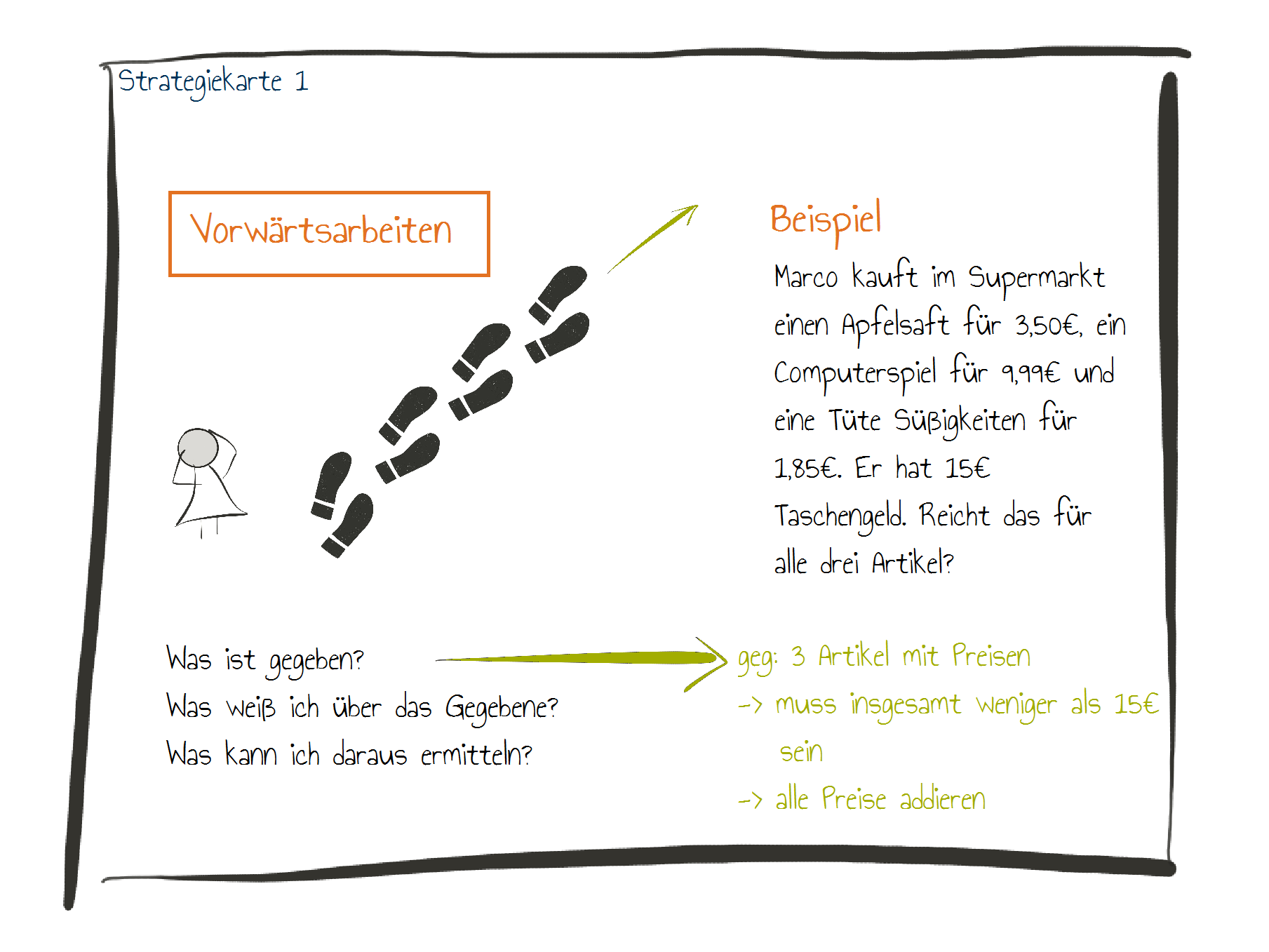
Überlegen Sie sich, ob das Erstellen einer Strategiekartensammlung etwas für Sie wäre. Gestalten Sie dann daraufhin eine Strategiekarte zu einem beliebigen Heurismus. Beachten Sie dabei, was ein Lernender auf solch eine Karte schreiben würde, ob Sie Beispiele verwenden möchten und wie kreativ Sie sein wollen.
Sie können Ihre Karte dann mit Ihren Kommilitonen vergleichen oder mit unserer Beispielkarte unten.
Aufgabe III
Rufen Sie sich eine klassische Problemlösesituation aus dem Unterricht ins Gedächtnis. Vielleicht haben Sie diese während Ihrer eigenen Schulzeit oder in einem Praktikum erlebt. Wählen Sie dann drei beliebige Gründe aus der Übersicht aus und versuchen Sie, diese in der Gestaltung der Unterrichtssituation zu entdecken. Vergleichen Sie Ihre Ergebnisse untereinander im Kurs oder mit der Beispiellösung.
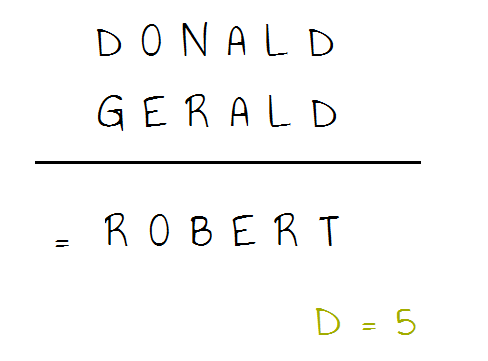
Wählen wir als Beispiel die bekannten Worträtsel. Durch die Möglichkeit, dieses Spiel mit verschiedenen Worten zu gestalten, wird die Neugierde der Lernenden geweckt. Sie lernen Durchhaltevermögen, wenn sie die richtige Lösung nicht auf Anhieb finden und immer wieder neue Wege probieren. Zum Schluß könnte die Kreativität geweckt werden, indem sich die Lernenden ein eigenes Rätsel dieser Art ausdenken sollen.
Aufgabe IV
In der App „König der Mathematik“ müssen Rechenaufgaben im Kopf gelöst werden. Für richtige Antworten erhält der Spieler Punkte und schaltet Level mit höherem Schwierigkeitsgrad frei. Bei falschen Antworten ertönt ein Signalton und die korrekte Antwort wird eingeblended. Am Ende jedes Levels gibt eine Übersicht Auskunft über die Anzahl der richtigen Antworten und die Gesamtpunktzahl.
Welche Merkmale eines intelligenten Computerprogramms erfüllt diese App? Sie können Ihre Antworten in Ihrem Kurs oder mit den Vorschlägen unten vergleichen.
a) Die Schwierigkeit kann kontinuierlich gesteigert werden.
b) Eine Lösung wird immer auf Richtigkeit geprüft. Die Lernenden erfahren, ob ihre Antwort richtig ist und werden in diesem Fall auch gelobt.
c) Bei einer falschen Antwort werden die Lernenden auf die Stelle hingewiesen, an der der Fehler entstand.
d) Am Ende einer Einheit können die Lernenden ihre Leistung einschätzen.
Aufgabe V
Sie überlegen, für eine Unterrichtseinheit zum Thema „Der Thaleskreis“ ein dynamisches Geometriesystem einzusetzen. Welche Vor- und Nachteile könnte der Einsatz haben?
Sie können Ihre Antworten in Ihrem Kurs oder mit den Vorschlägen unten vergleichen.
Vorteile:
- Exploratives und eigenständiges Arbeiten: Punkt auf dem Thaleskreis kann im Zugmodus selbstständig bewegt werden
- Abgabe von Routinetätigkeiten: Zeitaufwendiges Zeichnen mit Lineal und Zirkel im Heft wird vermieden
- Förderung von Problemlösestrategien: Erkennen der Invarianz des Winkels durch dynamische Darstellung, Vermutung über rechten Winkel, Verwendung von Hilfslinien zur Begründung
Nachteile:
- Werkzeuge zur Konstruktion und Umgang mit dem Programm müssen bekannt sein
- Überforderung durch gleichzeitiges Bearbeiten der Aufgabe und Werkzeugbedienung