Anforderungen an geeignete Probleme im Schulkontext

(Leuders, 2003; Tietze, Klika & Wolpers, 2000; Reiss & Hammer, 2013)

Nach Tietze, Klika und Wolpers (2000, S.96) gibt es hinsichtlich der Anforderungen an geeignete Problemstellungen Schüler-, Ziel- und Methodenbezogene Aspekte.

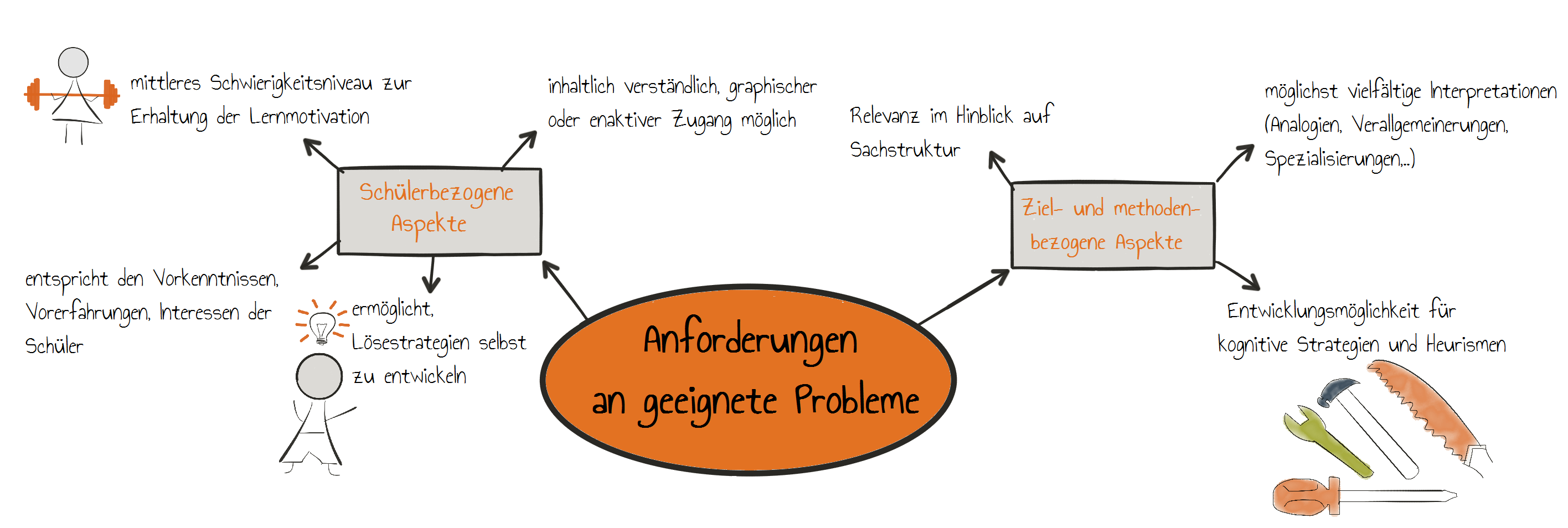
Was ist eine gute Problemlöseaufgabe?

Aufgaben und ihre Einsetzung können den Lernprozess der Lernenden initiieren und unterstützen. Nach Leuders (2003, S.123) bietet eine didaktisch gute Problemlöseaufgabe reichhaltige Tätigkeiten auf verschiedenen Ebenen, verschiedene oder neue Sichtweisen auf mathematische Inhalte und Vernetzungen und ist zugleich eine Anwendungsmöglichkeit für heuristische Strategien. Zusätzlich gilt:

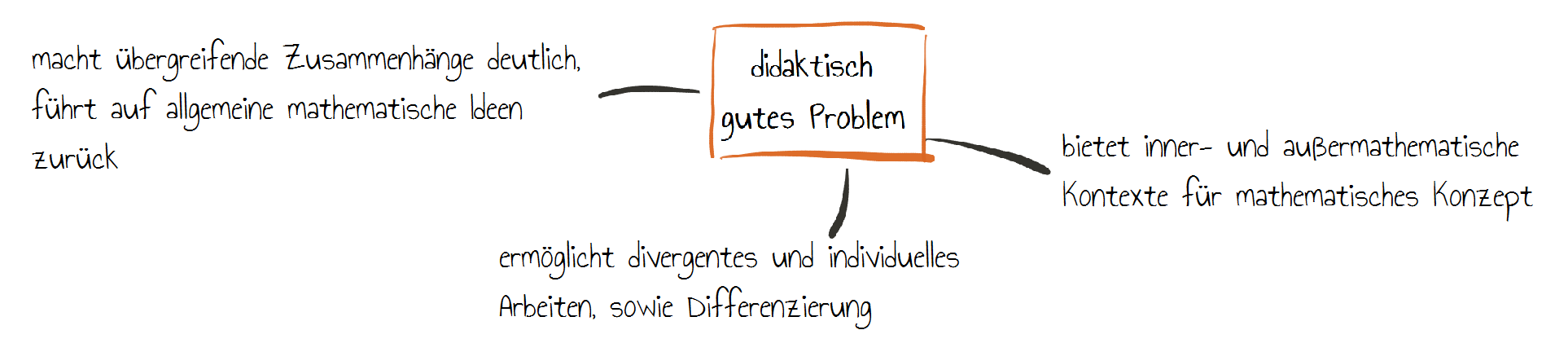
Mehr über Gestaltungsmerkmale von Aufgaben können Sie im Modul Kognitive Aktivierung - Unterrichtsplanung - Graphen und Bäume nachlesen. Hier geht es vor allem um die Gestaltung von kognitiv aktivierenden Aufgaben.

Videobeispiel

In Szene 7: Spannendes über Quadrat- und Dreieckszahlen bekommen die Lernenden den Arbeitsauftrag, die Zahlen von 1 bis 100 möglichst geschickt zu addieren. Diese Problemaufgabe erfüllt einige der oben genannten Kriterien. So ist sie beispielsweise dem Vorwissen der Lernenden angemessen, da dieser Typ Aufgabe nun schon eine Weile in den vorherigen Videos behandelt wurde. Die Lernenden können das Problem auf beliebige Weise lösen, daher wäre auch ein enaktiver oder ein graphischer Zugang denkbar. Das Problem lässt einige Verallgemeinerungen zu, da die Formel auch bei anderen Aufgaben einsetzbar ist. Diese Aufgaben finden Sie im fachwissenschaftlichen Teil des Moduls.

Schauen Sie sich das Video an. Zählen Sie auf, welche weiteren Kriterien Sie noch erkennen können.