Die Phasen des Modellierens
(Blum & Schukajlow, 2018; Borromeo Ferri, 2011; Greefrath et al., 2013; Reiss & Hammer, 2013; Schukajlow, 2006; Schukajlow-Wasjutinski, 2010; Verschaffel, Greer & DeCorte, 2000)
In Anbetracht dessen, dass Realitätsbezüge und mathematisches Modellieren in der jüngeren Vergangenheit deutlich an Gewicht gewonnen haben (vgl. Blum & Schukajlow, 2018) und das idealtypische dreischrittige (bzw. vierschrittige) Kreislaufmodell vermeintlich eher undifferenziert erscheint und nicht mehr dem aktuellen Forschungsstand entspricht, werden im Folgenden die sieben Phasen des Modellierens aus dem sogenannten DISUM-Modellierungskreislauf (vgl. Schukajlow-Wasjutinski, 2010) betrachtet. Das siebenschrittige Modell ist weitaus differenzierter und integriert alle oben genannten Aspekte.
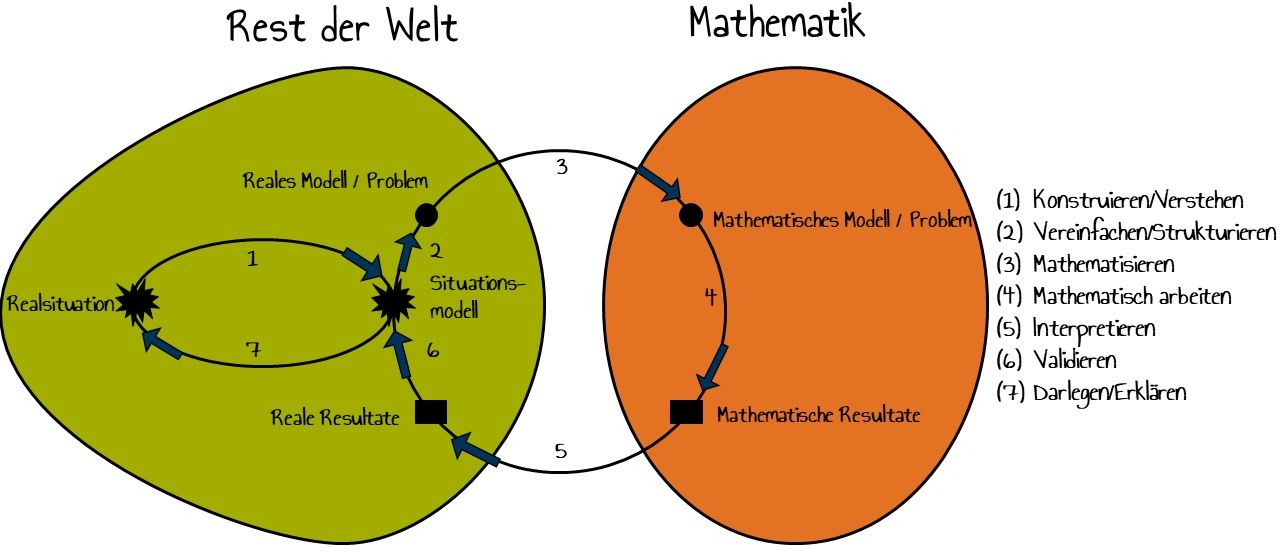 Abbildung: In Anlehnung an Schukajlow-Wasjutinski (2010, S. 76)
Abbildung: In Anlehnung an Schukajlow-Wasjutinski (2010, S. 76)
1. Verstehen/Erstellen eines entsprechenden fiktiven Modells
Der erste Schritt der Problemlösung einer Aufgabe hat das Lesen und das Verstehen der Aufgabe zum Ziel. Ohne diesen Schritt sind die Folgenden nicht durchführbar. Hierbei wird eine sogenannte „mentale Repräsentation“ (Schukajlow-Wasjutisnki, 2010, S. 77) der Aufgabe hervorgebracht. Die Basis hierfür sind der zugrundliegende Text, ein Situationsbild und das Vorwissen des Lernenden. Damit wird ein Situationsmodell gebildet, welches vom Vorwissen der Lernenden geprägt ist. Durch die durch die Textgrundlage geleitete selbstständige Strukturierung kommt das eigene Handeln und Wissen zur Geltung: Informationen werden exzerpiert und ergänzt und ein erstes Modell entsteht.
2. Vereinfachung/Strukturierung der (Problem-)Situation
Nun ist die Grundlage für den Modellierungsprozess geschaffen und es folgt ein weiterer Prozessabschnitt vor der Mathematisierung. Dabei wird das Situationsmodell zum Realmodell hin abgespeckt und konkretisiert. Dieser Vorgang der Reduzierung auf das Wesentliche wird durch das Eliminieren unbedeutender Passagen, die Bestimmung einer bisher nicht vorhandenen Größe im Sinne einer Variable und die Festlegung von Handlungsgefügen durchgeführt. Dabei werden die Gefüge auf ihre Mathematisierbarkeit hin überprüft. Liegt dem Lernenden eine eher einfache Aufgabe vor, ist dies nicht unbedingt ein eigenständiger Schritt.
3. Mathematisieren des Realmodells
Nach der Überführung in ein Realmodell folgt die Überführung in ein mathematisches Modell. Dabei wird ein weiteres Modell geschaffen, das die bisher in Erfahrung gebrachten Zusammenhänge in mathematische Zusammenhänge überträgt.
4. Innermathematischer Schritt: Mathematisches Arbeiten
Ist es an dieser Stelle bereits möglich, eine Schlussfolgerung zu ziehen, wird dieser Schritt als mathematisches Arbeiten bezeichnet. Hierbei können unterschiedliche Schwierigkeitsgrade entstehen, wie etwa beim Satz des Pythagoras, was sodann einige Fähigkeiten voraussetzt. Das mathematische Objekt, zumeist eine Zahl, ist dann der Ausgang des mathematischen Arbeitens. An dieser Stelle gilt es, das mathematische Ergebnis zurück auf die Ebene des Modells zu übersetzen. Zum innermathemathischen Schritt des Beweisens und Argumentieren und zu Beispielen zur Satzgruppe des Pythagoras sei auf das Modul Feedback - Beweisen und Argumentieren - Der Satz des Pythagoras verwiesen.
5. Interpretation des mathematischen Resultats
Die Überführung des mathematischen Ergebnisses in die Ebene des Real- und Situationsmodells wird als Interpretation bezeichnet. Es besteht bereits bei diesem Prozessabschnitt die Möglichkeit, die bisherigen Resultate zu prüfen und womöglich erneut ein mathematisches Modell zu konstruieren. Dies wird jedoch zumeist für den folgenden Schritt vorgesehen.
6. Übertragung in ein reales Ergebnis/Validierung des Resultats
Sowohl das Realmodell als auch das Situationsmodell können nun Objekte der Ergebnisinterpretation sein. Vermag das reale Resultat die Aufgabenfrage zu beantworten, dann kann hier der Kreis geschlossen werden. Validieren bedeutet in diesem Kontext die Ergebniskontrolle und die Ergebnisbewertung. Sollte der Fall auftreten, dass der Überprüfungsvorgang nicht zufriedenstellend ist, sind die Lernenden veranlasst, die gebildeten Modelle auf ihre Qualität hin zu überprüfen.
7. Vermittlung: Darlegen/Erklären
Abschließend sollen das Ergebnis und der Lösungsweg aufgezeigt werden, was meistens bereits während der Gestaltung des Situationsmodells und des Realmodells geschieht.
Empirische Ergebnisse zu den Teilschritten der Lernenden
Zahlreiche Untersuchungen zeigen, dass jeder Teilschritt des Modellierungsprozesses bereits eine kognitive Hürde für Lernende darstellt.
Besonders beim ersten Schritt, dem Verstehen der Realsituation und dem Bilden eines geeigneten Modells, haben Lernende große Schwierigkeiten. Viele Lernende haben es sich im Laufe ihrer Schulzeit angewöhnt, die erste Teilkompetenz zu umgehen, indem sie Ersatzstrategien anwenden. Dabei wird der Kontext ignoriert und nur die gegebenen Zahlen aus der Aufgabe mit einem beliebigen Schema verrechnet (vgl. Verschaffel, Greer & DeCorte, 2000).
Auch das Validieren wird von Lernenden als schwer empfunden. Sie überprüfen ihre Lösungen meist nicht von selber. Vielmehr scheinen Lernende die Einstellung zu haben, dass das Überprüfen in den Zuständigkeitsbereich der Lehrenden fällt.
Borromeo Ferri (2011) stellte fest, dass der individuelle Modellierungsprozess der Lernenden mitunter stark von den theoretisch entwickelten Kreisläufen abweicht. Vielmehr durchlaufen Lernende gewisse Phasen mehrfach und/oder lassen andere dafür aus. Sie springen zwischen den Phasen hin und her. Dabei sind die individuellen Vorgehensweisen geprägt vom mathematischen Denkstil der Lernenden (z. B. visueller oder analytischer Denkstil).
Videobeispiel
Betrachten Sie untenstehendes Video Szene 1: Hausaufgabenbearbeitung der Modellierungsaufgabe. Die Schülerin hat ein Milchsäurebakterienwachstum, welches sie graphisch darstellen soll. Die zweite Phase, das Vereinfachen des Problems, steckt hier bereits in der Aufgabenstellung. Es wird angenommen, dass sich alle Bakterien gleich vermehren, dass die Temperatur konstant bleibt, dass die Milchmenge gleicht bleibt, etc. Diese Faktoren, die die Bakterienvermehrung beeinflussen könnten, können im mathematischen Modell nicht berücksichtigt werden. Der Entschluss der Schülerin, das Wachstum zunächst einmal mit einem exponentiellen Wachstum zu beschreiben, startet dann die Phase des Mathematisierens.
Welche weiteren Phasen können Sie in diesem Video erkennen?