Entwicklung des Modellierungsprozesses
(Böhm, 2013; Borromeo Ferri, 2011; Maaß, 2004; Niss et al., 2007; OECD, 2003; Pollak, 1977)
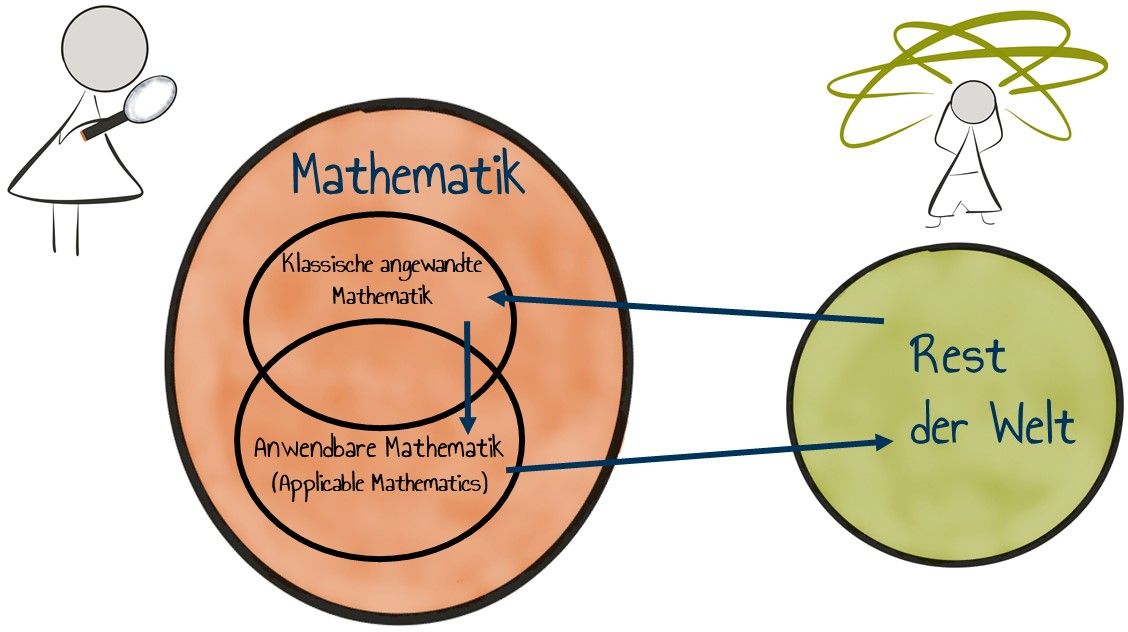
Das mehrschrittige mathematische Modellieren ist ein Bearbeitungsprozess, der zumeist Modellierungsprozess genannt wird. Auf internationaler Ebene wird dieser Vorgang als ‘mathematical modelling’ bezeichnet (vgl. Niss et al., 2007). Entsprechend dem PISA-Framework (OECD, 2003, S. 38) wird ein solcher Kreislauf mit den Bezeichnungen ‘real-world problem’, ‘mathematical problem’, ‘mathematical solution’ und ‘real solution’ angegeben, der letztlich mit dem Ausdruck ‘mathematical cycle’ benannt wird. Die Trennung zwischen der Mathematik und der „Welt“ ist auf den amerikanischen Mathematiker Henry O. Pollak (1977) zurückzuführen:
Borromeo Ferri (2011, S.14 ff.) unterscheidet vier Arten von Modellierungskreisläufen. Ihre Klassifizierung erfolgt nach den deutlichsten richtungsweisenden Unterschieden zwischen „Realer Situation (RS) und Situationsmodell (SM) beziehungsweise zwischen Mentaler Situations-Repräsentation (MSR), Realem Modell (RM) und Mathematischem Modell (MM)“ (ebd., 14):
-
Modellierungskreisläufe der angewandten Mathematik (dreiphasig): Dieser Kreislauf subsummiert einige Ansätze der Modellierungsauffassungen und es besteht keine Phase zwischen der realen Situation und dem mathematischen Modell. Dieser Typus fußt auf den komplexen mathematischen Problemtypen.
-
Didaktische Modellierungskreisläufe (vierphasig): Dieser Typus richtet sich nach dem Grad der Anwendbarkeit im Schulunterricht und erfährt eine Erweiterung durch einen Prozessschritt, dem realen Modell (RM). Er eignet sich nach Maaß (2004) insbesondere für die höheren Klassenstufen.
-
Modellierungskreisläufe zur Rekonstruktion des Situationsmodells bei Textaufgaben (fünfphasig): Wie der Name bereits verdeutlicht, richtet sich dieser Typus auf die Bearbeitung von Textaufgaben im Schulunterricht, bei dem Textinhalte repräsentiert werden. Der vierphasige didaktische Modellierungskreislauf wird um den Aspekt eines Situationsmodells ergänzt, der auch Problemmodell genannt wird. Dies ist auf der Grundlage unterschiedlicher Theorien, seien es solche über Problemlösungen oder des Textverständnisses, entstanden.
-
Diagnostischer Modellierungskreislauf (sechsphasig): Hierbei wird das Situationsmodell von der mentalen Situations-Repräsentation unterschieden. Diese Weiterentwicklung des dritten Typus verhilft individuellen Einflussgrößen des Modellierenden (u. a. Lesekompetenz, Vorwissen, kognitive Aspekte) zu mehr Verständnis.