Kumulatives Lernen
(Bruder et al, 2015; Käpnick, 2014; Tietze, Klika & Wolpers, 1982; Reiss & Hammer, 2013)
Unter dem kumulativen Lernen versteht man nach Reiss & Hammer (2013) den Wissens- und Kompetenzaufbau, der im Laufe der Schulzeit ein immer tiefer gehendes Verständnis von mathematischen Inhalten und Methoden erzeugt, wobei vorhandenes Wissen und bereits erworbene Kompetenzen berücksichtigt werden. Vernetzungen zu anderen Inhalten spielen ebenfalls eine große Rolle.
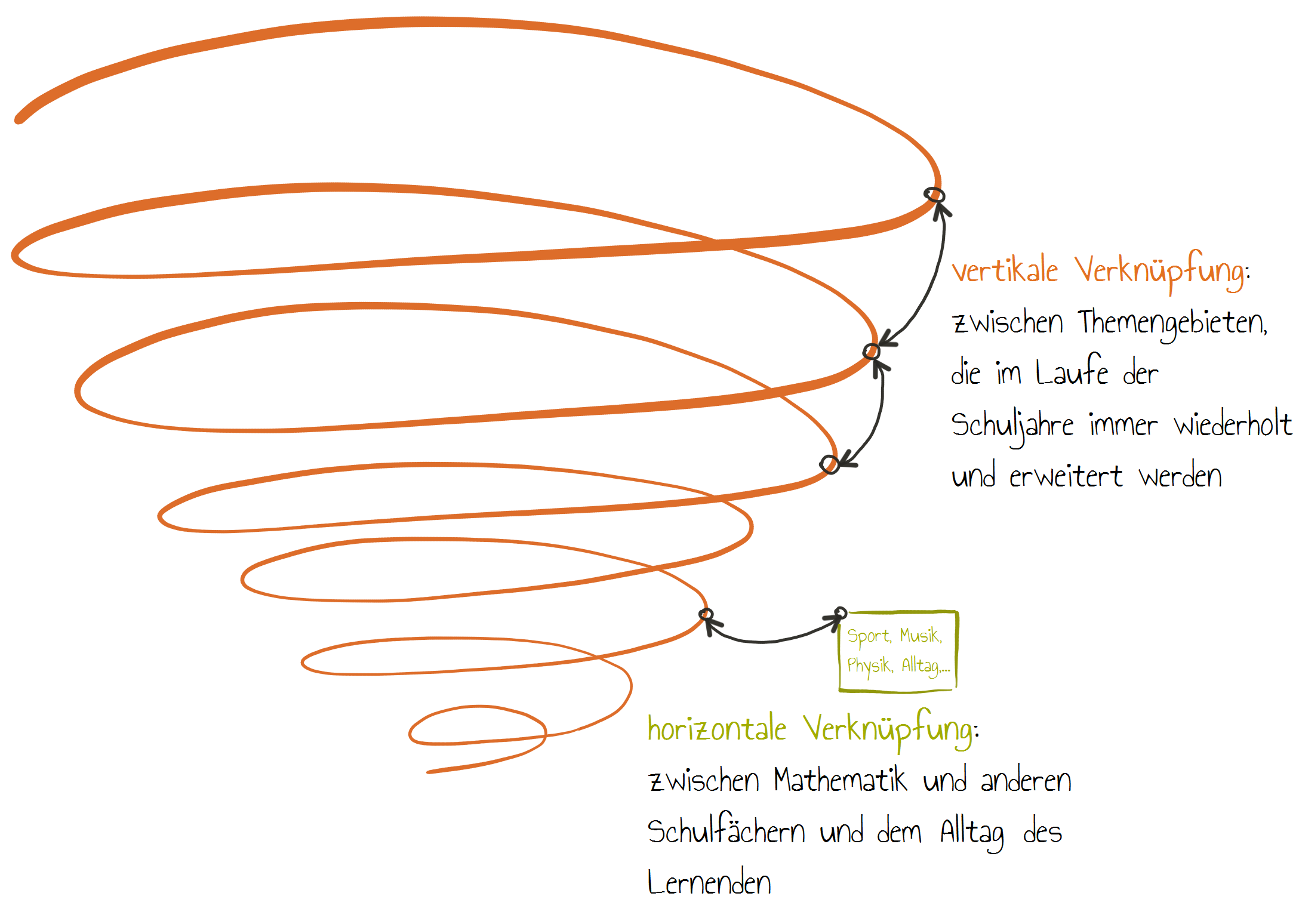
Dieses Prinzip ist eng mit dem Spiralprinzip verknüpft. Dabei wird aber, im Gegensatz zu dem Spiralprinzip, zwischen zwei Vernetzungsebenen unterschieden, nämlich der vertikalen und horizontalen Ebene. Bei der vertikalen Vernetzung liegt der Fokus auf der Weiterentwicklung und der Verknüpfung unterschiedlicher Themengebiete der Mathematik im Laufe der Schuljahre. Weiter bezieht sich das horizontale Verknüpfen auf eine fächerübergreifende Verknüpfung. Hier werden zum Beispiel mathematische Kenntnisse gebraucht, um physikalische Aspekte zu erschließen. Die horizontale Verknüpfung schließt auch die Verbindung zwischen Schulwissen und Alltag ein.
Beispiele
- Der Ergänzungsbeweis des Pythagoras aus dem Modul 1 Feedback - Beweisen und Argumentieren - Der Satz des Pythagoras eignet sich gut für horizontale Verknüpfungen.
Überlegen Sie sich, welche Aspekte der Mathematik dabei miteinander verknüpft werden.
- In Szene 2 - gemeinsame Erarbeitung der graphischen Ableitung des Sinus - Teil 2 ist eine Anwendung der vertikalen Verknüpfung zu sehen. Die Eigenschaften einer Achsenspiegelung werden angewandt, um die Steigung der Tangenten in dem gespiegelten Punkt herauszufinden. Dadurch werden verschiedene Themengebiete der Mathematik verbunden.
Integrationsprinzip / Lernen in Zusammenhängen:
(Bruder et al, 2015; Käpnick, 2014; Tietze, Klika & Wolpers, 1982)
Wissen wird im Gedächtnis als ein Netzwerk von Begriffen und Beziehungen gespeichert, daher muss Lernen unbedingt in Beziehungsnetzen und Sinnzusammenhängen stattfinden.
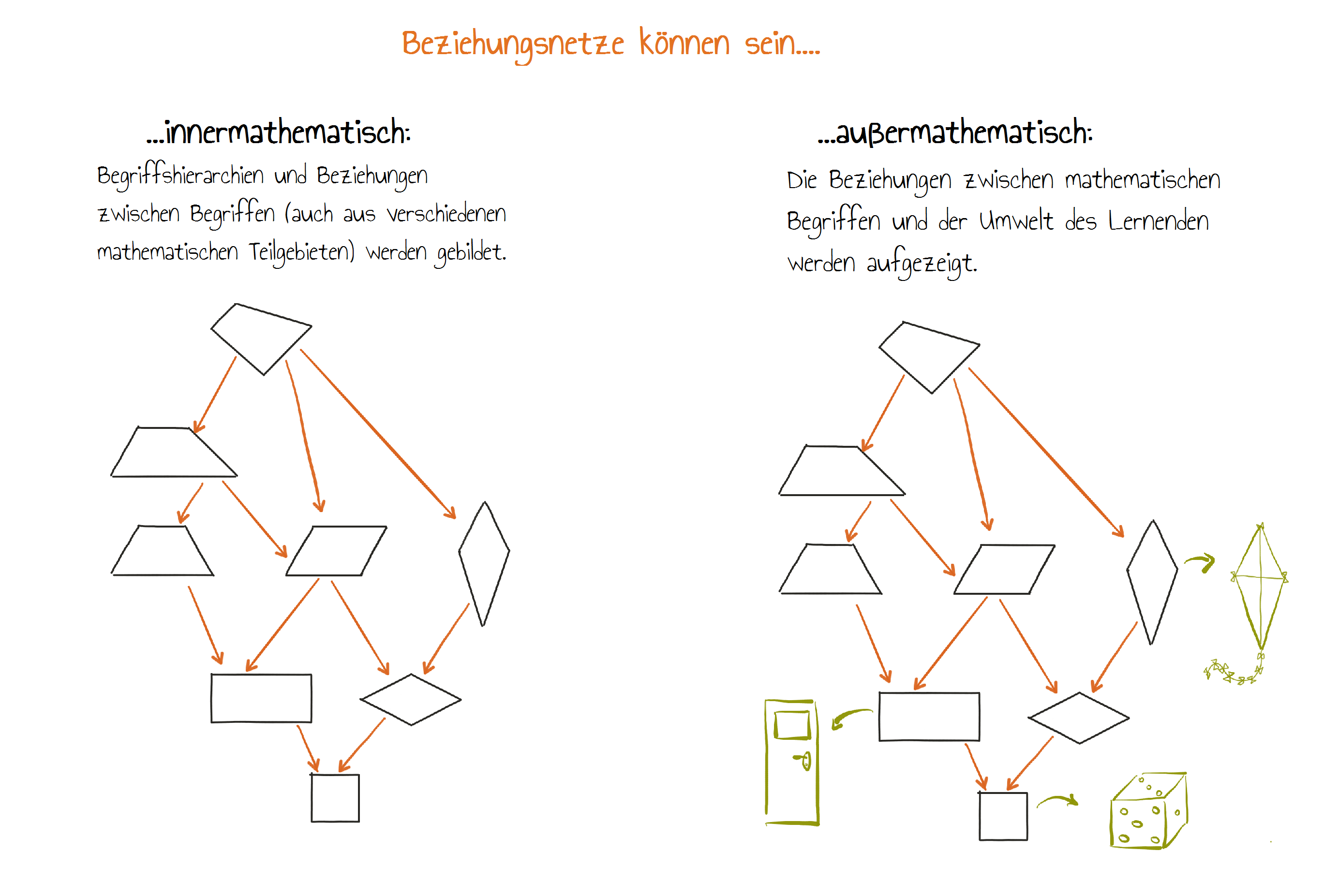
Entwickeln sich vertikale Verknüpfungen zwischen verschiedenen Themengebieten, so handelt es sich um kumulatives Lernen.
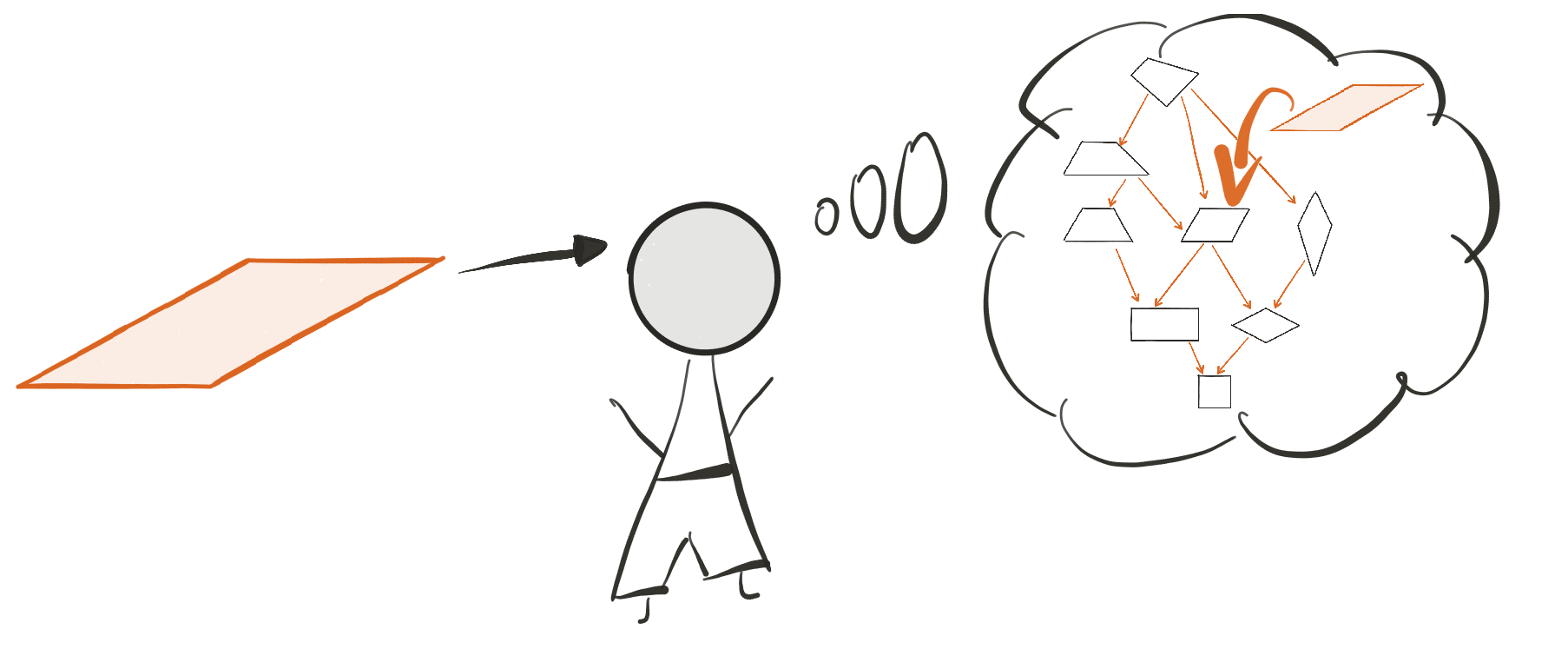
Lernen sollte stets in Sinnzusammenhängen stattfinden. Neue Lerninhalte sollten dabei in bereits vorhandene Wissensnetze integriert werden. Diese Beziehung muss im Unterricht deutlich gemacht werden.
Diese Art der Einbettung in bereits vorhandenes Wissen wird beispielsweise im fachwissenschaftlichen Teil des Moduls an der Taylor-Entwicklung des Sinus verdeutlicht. Hierbei wird vorausgesetzt, dass die Lernenden bereits mit der Sinusfunktion und seiner Ableitung vertraut sind. Nun lernen sie zusätzlich eine andere Darstellung des Sinus kennen und können das neuerlernte Wissen in ihr vorhandenes Beziehungsnetz eingliedern.