Unterrichtsplanung
(Tietze, Klika & Wolpers, 1997)
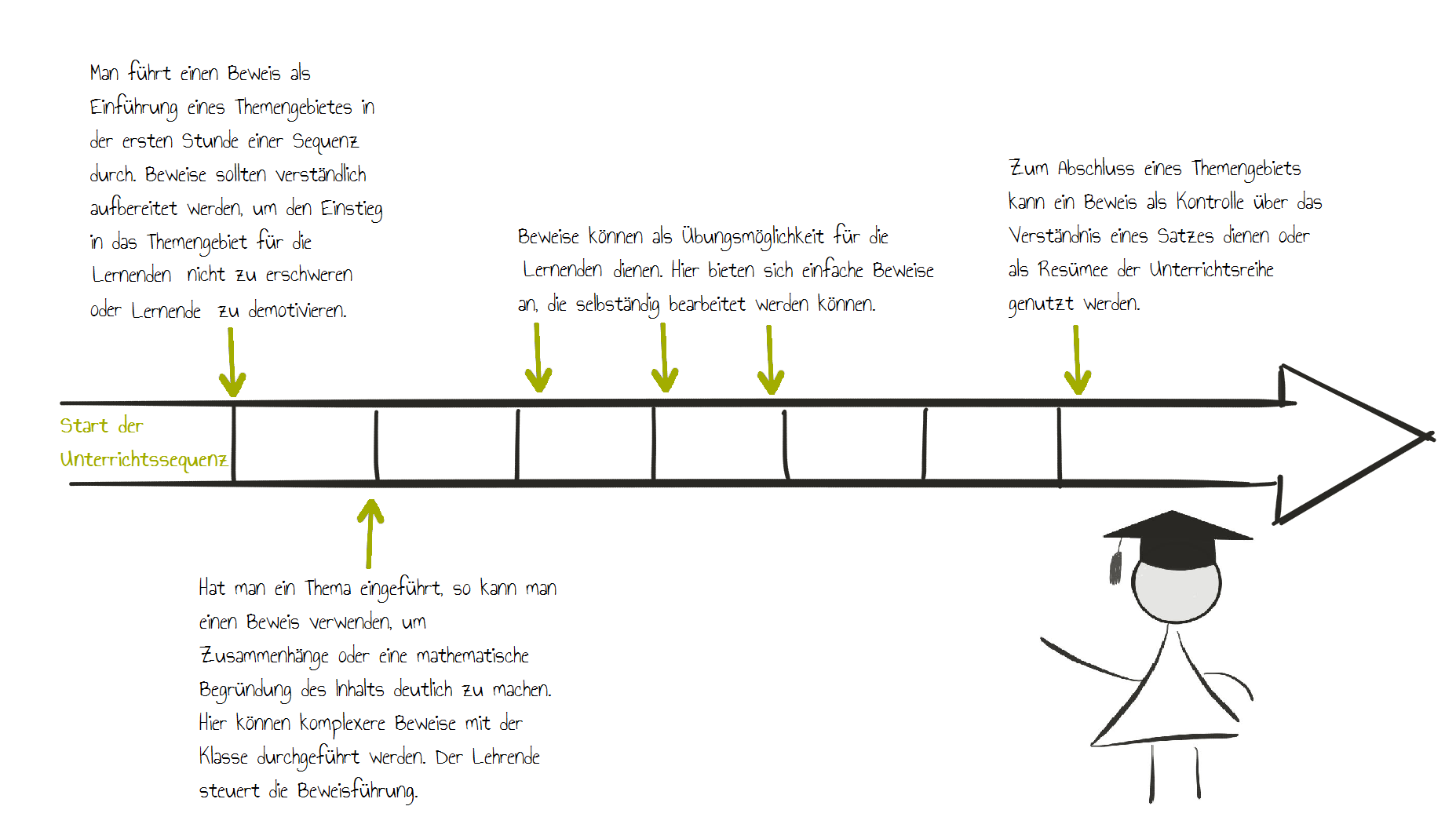
Positionierung von Beweisaufgaben in einer Unterrichtssequenz
Eine Unterrichtssequenz setzt sich in der Regel aus mehreren Unterrichtseinheiten zusammen. Hat man sich für einen Beweis entschieden, so ist zu überlegen, in welche dieser Einheiten die Beweisaufgabe eingebaut wird.
Hierzu gibt es verschiedene Möglichkeiten:
Auswahl geeigneter Themen
Nach welchen Kriterien wählt man Unterrichtsinhalte zum Beweisen und Argumentieren aus? Welche eignen sich mehr, welche weniger?

Beweise und Argumentationen werden im Unterricht oft im Themengebiet der Geometrie durchgeführt. Inhalte können hier meist anschaulich dargestellt werden.
Auswahl geeigneter Aufgaben
Generell kann jede Aufgabe zu einem Argumentationsanlass werden, wenn sie als Zielsetzung die entscheidenden Merkmale aufweist. Außerdem sollte nicht eine einzige Aufgabe zum Erlernen von Beweisen verwendet werden. Vielmehr geht es darum, eine Beweis- und Begründungskultur im Unterricht zu etablieren, die durch konstante kognitive Aktivierung der Lernenden und gezieltem Hinterfragen aufgebaut wird.
Üblicherweise beginnen alle Arbeitsaufträge mit:
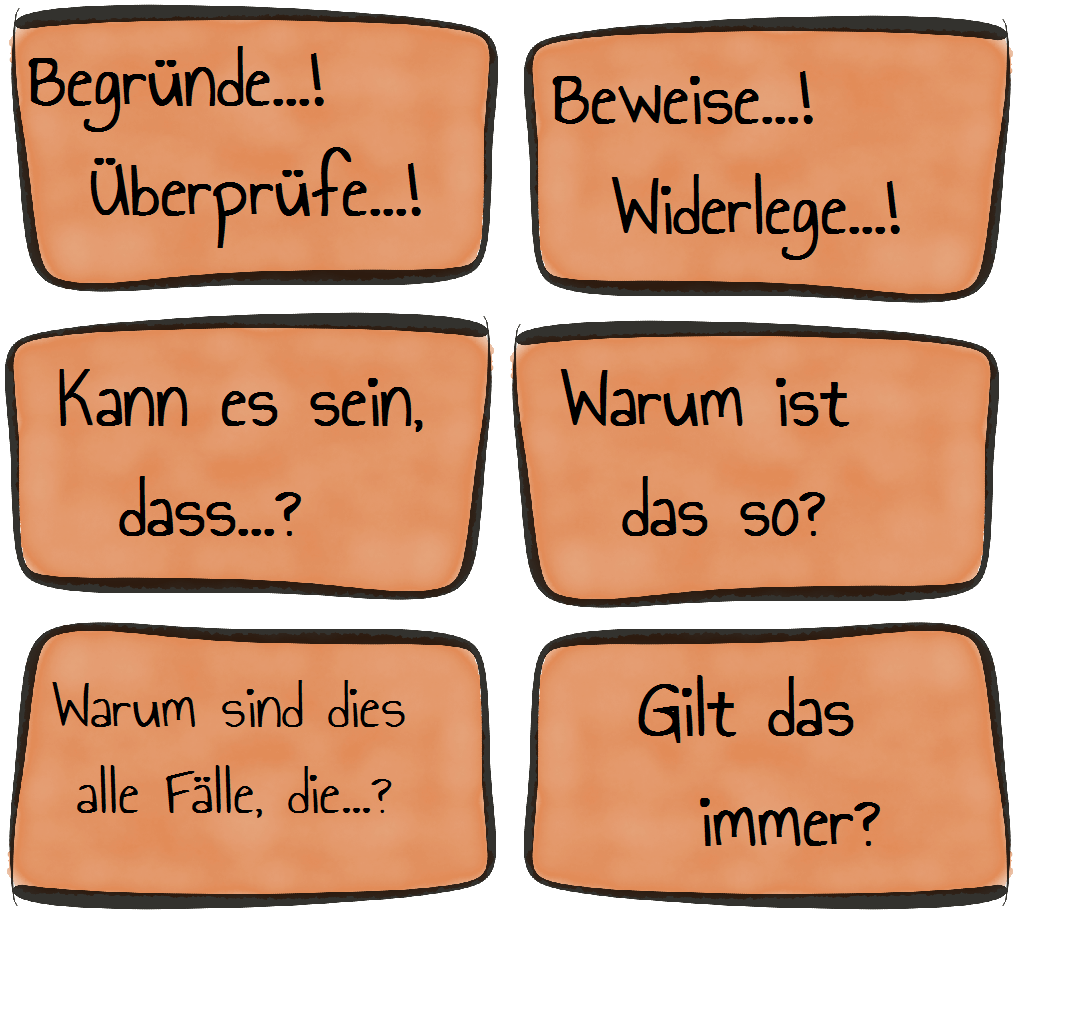
Auch Probleme dienen als Ausgangspunkt eines Beweises oder einer Argumentation. Mehr zum Thema Problemlösen können Sie in unserem Modul Motivation - Problemlösen - Quadrat- und Dreieckszahlen nachlesen.
Einen ausführlichen Überblick in das Thema Unterrichtsplanung erhalten Sie im Modul Kognitive Aktivierung - Unterrichtsplanung - Graphen und Bäume.
Videobeispiel
Das Verstehen mathematischer Zusammenhänge ist für das Entwickeln eigener Beweise von Vorteil. Die algebraischen Formeln eignen sich gut, um einen Zusammenhang zwischen der Geometrie und Algebra herzustellen. Beobachten Sie dies in Szene 5: Visualisierung algebraischer Formeln.
Kriterien für einen didaktisch guten Beweis
(Tietze, Klika & Wolpers, 1997)
Bei der Vielzahl der verschiedenen Beweise zu einem Thema, stellt sich die Frage, welcher davon sich besonders für den Unterricht eignet. In der Grafik sehen Sie einen Überblick über die verschiedene Kriterien von Tietze, Klika & Wolpers (1997, S.175), die ein gewinnbringender Beweis erfüllen soll und die damit die Auswahl beeinflussen können.
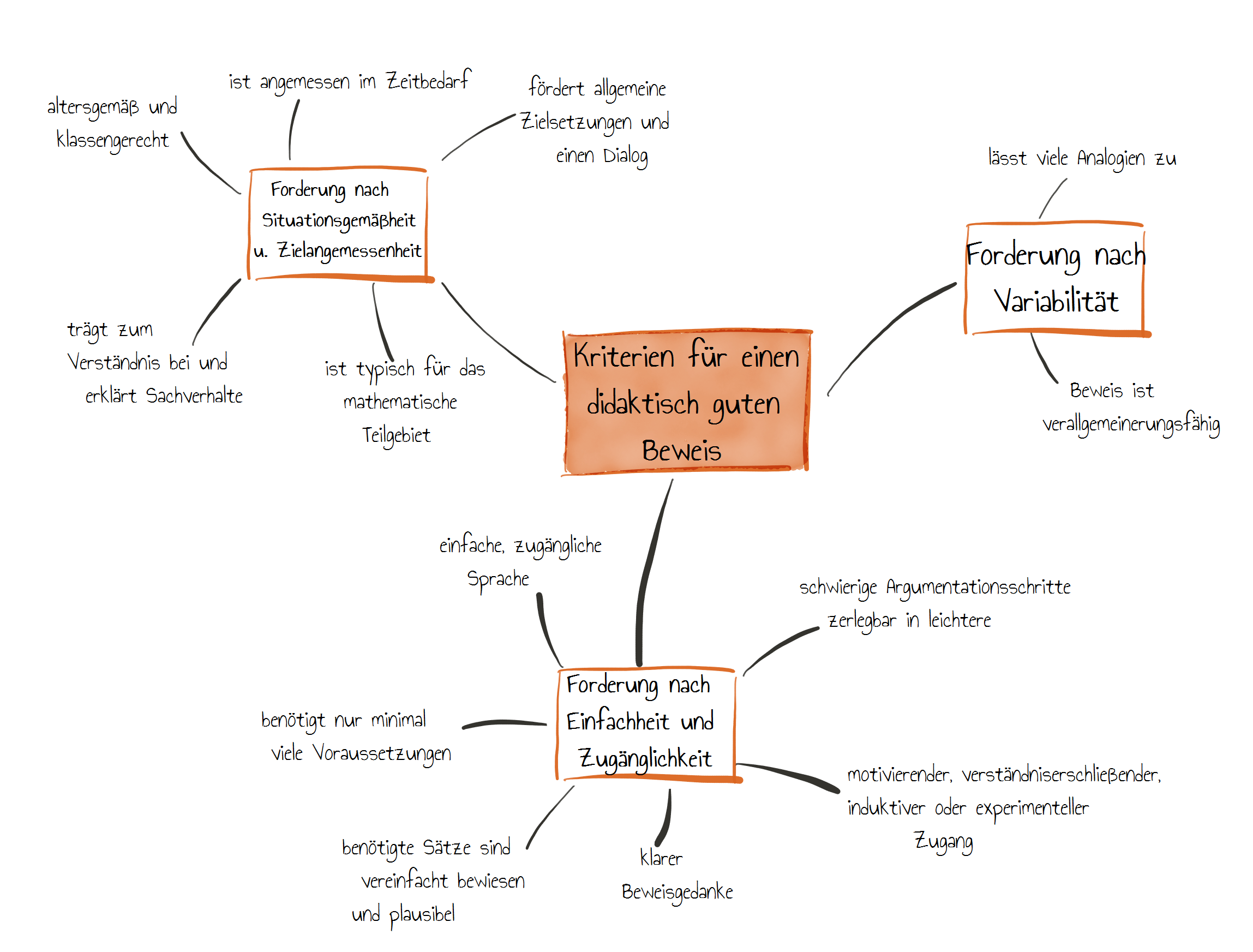
Beispiel
Der Ergänzungsbeweis aus dem fachwissenschaftlichen Teil dieses Moduls erfüllt einige dieser Kriterien. Ein experimenteller Zugang mit ausgeschnittenen Quadraten und Dreiecken (oder mit unseren dynamischen mathematischen Visualisierungen) ist denkbar. Der Beweisgedanke ist relativ klar und, da kaum Sätze in den Beweis einfließen, benötigt er nicht viele Voraussetzungen. Da es sich um die Verbindung eines geometrischen und arithmetischen Beweises handelt, kann hier auch die volle Spannbreite dieses mathematischen Teilgebiets gezeigt werden.
Betrachten Sie das Beispiel des Ergänzungsbeweises. Überlegen Sie sich, welche weiteren Kriterien aus der Grafik noch erfüllt werden.