Warum Beweise im Unterricht sinnvoll sind
(Brunner, 2014; de Villiers, 1990, 1991; Tietze, Klika & Wolpers, 2000)
Gründe für das Beweisen und Argumentieren im Unterricht
Warum ist es so wichtig, im Unterrichtsalltag regelmäßig Beweise einzubauen, obwohl sie zeitaufwendig sind und für die Lernenden sehr anspruchsvoll sind? In der Grafik sehen Sie, warum nach Tietze, Klika & Wolpers (2000, S.167) die Lernenden dennoch vom Beweisen profitieren können.
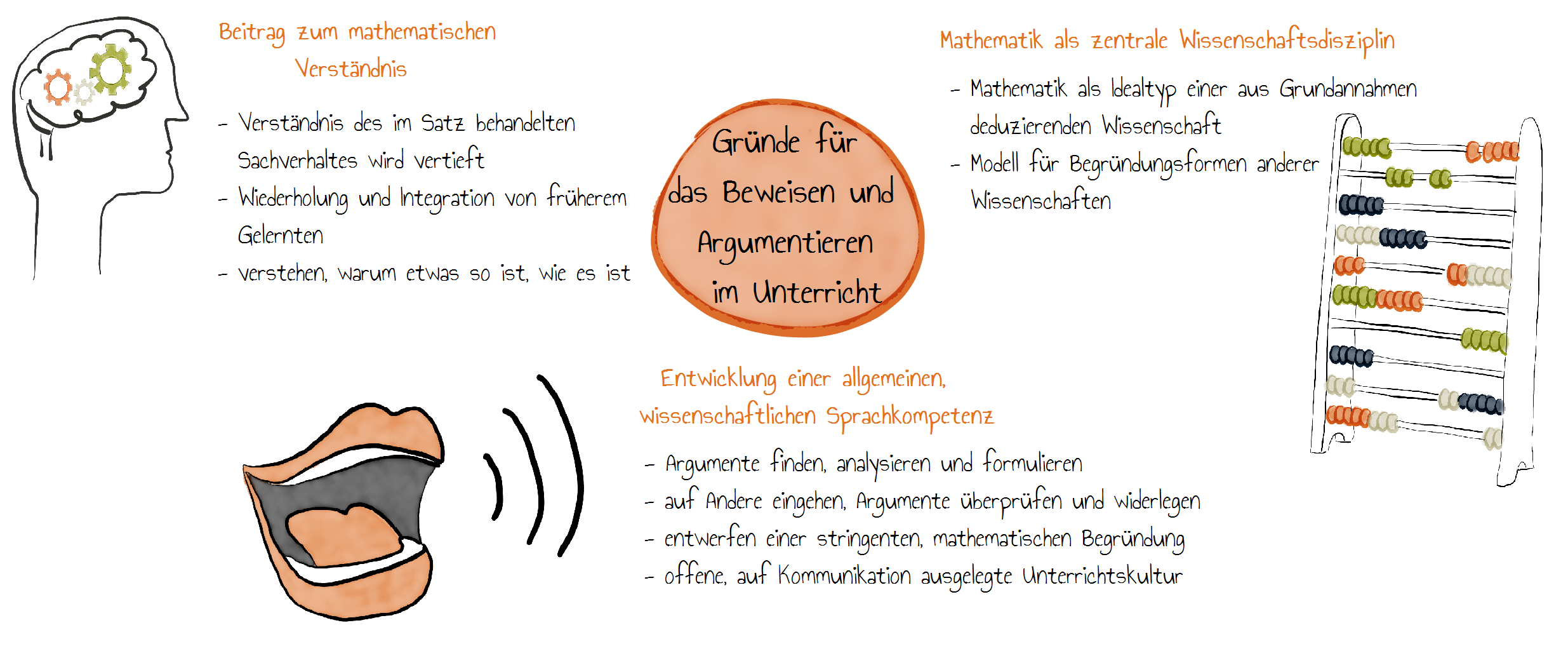
Funktionen von mathematischen Beweisen im Unterricht
(de Villiers, 1990, 1991)
Die Lernenden entwickeln nach de Villiers (1990, S.18 ff.) durch die Beschäftigung mit Beweisen im Unterricht sechs grundlegende Kompetenzen. Die folgende Abbildung beruht auf der Übersetzung von Brunner (2014, S.14).
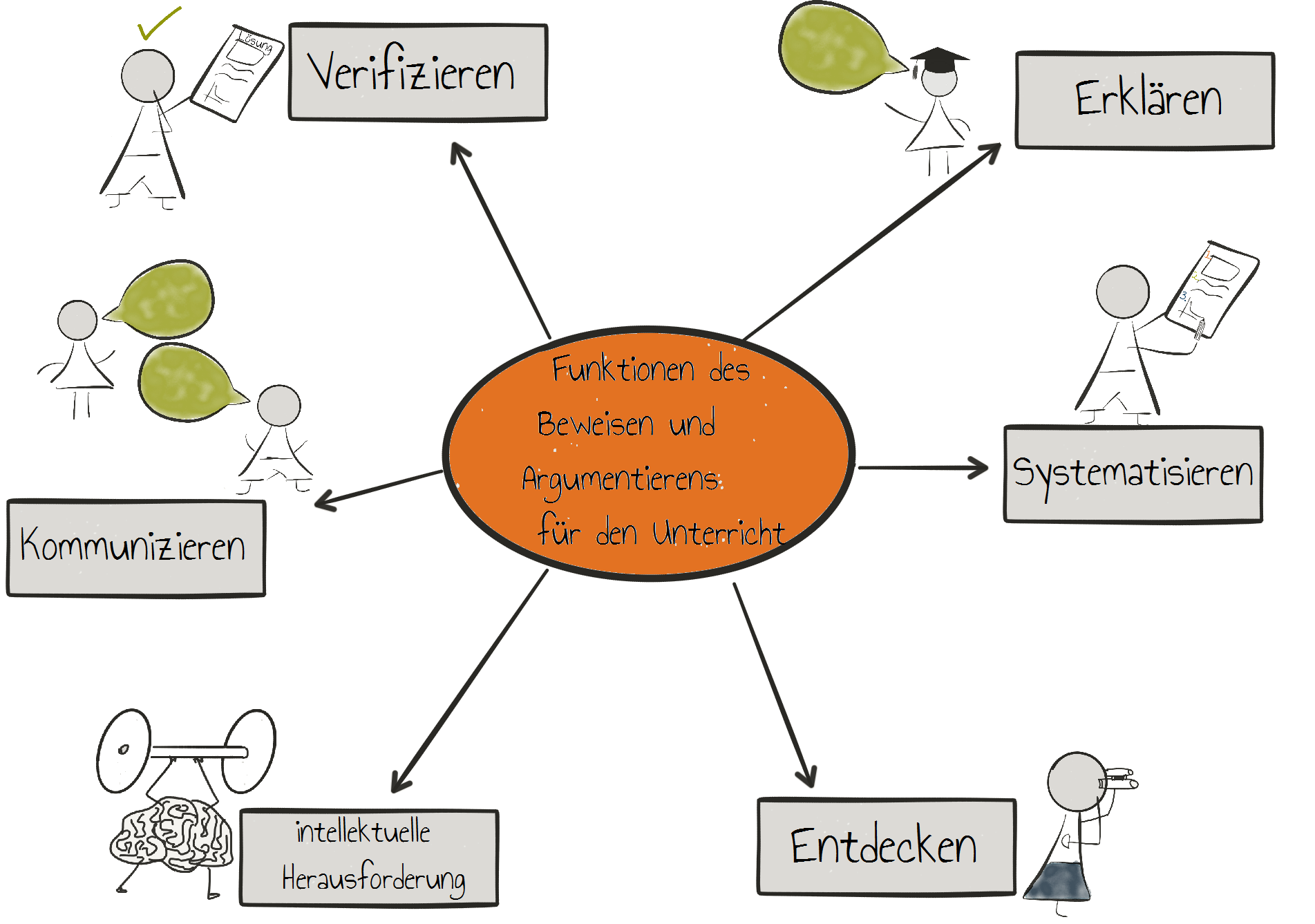
-
Verifizieren: Durch deduktives Schließen wird eine Aussage sicher begründet und die Behauptung wird bestätigt.
-
Erklären: Es wird Einsicht vermittelt, warum die Aussage wahr ist und unter welchen Voraussetzungen sie gilt. Dies kann insbesondere mit inhaltlich, anschaulichen und handlungsbezogenen Beweisen erreicht werden.
-
Systematisieren: Bekannte Definitionen, Sätze und Begriffe werden in Beziehung zueinander gesetzt, vernetzt und dadurch in ein umfassendes deduktives System eingeordnet.
-
Entdecken: Neue Phänomene und Aussagen werden durch den Beweisprozess gefunden, der Beweis ist hierbei Mittel zum Erkennen und Erforschen von Zusammenhängen sowie zur Entwicklung neuer Begriffe. Der Begründungsvorgang wirkt kognitiv aktivierend. Lernende können selbst Zusammenhänge entdecken.
-
Kommunizieren: Denkprozesse und Argumentationen werden verbalisiert. Der Beweis ist ein wesentlicher Prozess bei der Kommunikation über mathematische Inhalte und ein Mittel des rationalen Argumentierens.
-
Intellektuelle Herausforderung: Die Lernenden werden kognitiv gefordert und entwickeln sich weiter.
Beweise dienen daher nicht nur der Sicherung mathematischen Wissens, sondern auch dem Verstehen. Sie sollten nicht alleine für sich stehen, sondern in ein Netz mathematischer Aktivitäten eingebunden sein, um die Verknüpfung zwischen diesen beiden Komponenten zu fördern. Dies bedeutet für den Unterricht, dass Beweisen nicht nur auf die Verifizierungsfunktion reduziert werden sollte, sondern vielmehr als Anlass genutzt wird, um das Verbalisieren von Erklärungen zu trainieren.
Für eine tieferes Verständnis zum Thema Beweisen bietet sich die Beweisübersicht zum Thema des Satz des Pythagoras und die Theorie im fachwissenschaftlichen Teil des Moduls an.