Die Lotka-Volterra-Regeln
(Begon, 2017; Lotka, 1929; Volterra, 1931; Wirsching, 2006)
Die Lotka-Volterra-Gleichungen des vorhergehenden Abschnitts wurden von Vito Volterra (1931) und Alfred J. Lotka (1929) unabhängig voneinander beschrieben und mathematisch analysiert. Als vereinfachtes Modell stellen sie die Grundlage für die Beschreibung diverser Räuber-Beute-Beziehungen in der Natur dar (Begon, 2017). Diese Gleichungen beruhten auf den Annahmen,
- dass die Beutepopulation proportional zur eigenen Zahl wächst, aber mit zunehmender Zahl an Räubern dezimiert wird, und
- dass die Räuberpopulation proportional zur eigenen Zahl ausstirbt, sich jedoch mit zunehmender Zahl an Beutetieren mehr und mehr vermehren kann.
Aus der mathematischen Beschreibung der Entwicklung von Räuber- und Beutepopulation lassen sich die drei Lotka-Volterra-Regeln ableiten; drei herausstechende mathematische Eigenschaften (Volterra, 1931), welche für den Biologieunterricht qualitativ formuliert werden:
Regel 1: Periodizität
Beide Populationen verändern sich periodisch. Sprich, nach einer bestimmten Zeit sind beide Populationen genauso groß wie zuvor.
Regel 2: Erhaltung der Mittelwerte
Beide Populationen schwanken um einen Mittelwert, welcher über die Zeit hin konstant bleibt.
Regel 3: Störung der Mittelwerte
Werden beide Populationen um denselben Faktor reduziert, so erholt sich die Beutepopulation schneller.
In Szene 5: Partnerarbeit mit einer Simulation erarbeiten sich Lutz und Clarissa die Regeln 2 und 3 anhand einer Simulation.
Das Aufgabenblatt aus dem Video: Download
Eine leicht vereinfachte Version dieser Simulation ist hier zu sehen.
Anleitung: An den Schiebereglern die Anzahl der Hasen und der Eulen zu Beginn der Simulation und die Reproduktionsrate der Hasen festlegen. Ein Klick auf den “Start”-Knopf startet die Simulation. Anschließend zeigen die blauen Punkte und der blaue Graph die Hasenpopulation; die orangenen Punkte die Eulen. Die gestrichelten Linien in den Graphen repräsentieren die Durchschnittswerte der Populationen. Der “20%”-Knopf reduziert beide Population instantan auf 20% der aktuellen Anzahl. Ein Klick auf den “Stop”-Knopf beendet die Simulation.
Die Originalversion findet sich hier: Download.
Der große Vorteil einer solchen Simulation für die Lernenden besteht darin, dass sie die genannten Effekte selbst explorativ entdecken können. Insbesondere der Effekt einer Störung der Mittelwerte ist in einer dynamischen Darstellung deutlicher zu sehen als in einem statischen Bild. Diese Simulationen können auch als Diskussionsgrundlage dienen: einerseits für das Modell an sich; andererseits auch für die Auswirkungen der Parameter. So erlaubt die obige Simulation die Reproduktionsrate der Beutetiere zu verändern und zu beobachten, welchen Einfluss dies auf Beziehung beider Populationen hat. Und auch wenn dies rein formal aus den Lotka-Volterra-Gleichungen hergeleitet werden kann, so kann es gerade für den Biologieunterricht interessanter sein, diesen Effekt direkt beobachten zu können.
Das Lernvideo, das in Szene 4: Einstiegsphase mit Lernvideo eingesetzt wurde und die Thematik kompakt für den Schulunterricht aufbereitet, finden Sie hier: Link.
In diesem Kontext sei erwähnt, dass sich die Lotka-Volterra-Regeln auch an dem Phasendiagramm aus dem vorhergehenden Abschnitt erschließen lassen. Dort wurden die Populationszahlen in ein Koordinatensystem eingezeichnet, wobei die Anzahl der Beute dem $x$-Wert und die der Räuber dem $y$-Wert entsprach. Den Differentialgleichungen folgend bewegte sich dann ein Punkt auf einer bestimmten Bahn.
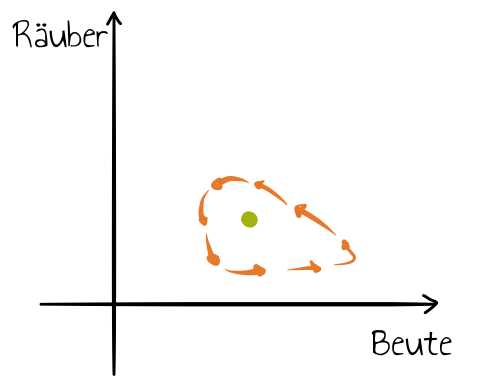
Regeln 1 und 2 können schon an diesem Phasendiagramm direkt abgelesen werden: Da die Bahnen alle geschlossen waren, bewegen sich beide Populationszahlen immer wieder durch denselben Punkt; und da die Bahnen sich nicht ändern, müssen beide Koordinaten um einen festen Mittelwert schwanken. Regel 3, die Störung der Mittelwerte, ist nicht ganz so offensichtlich. Allerdings ermöglichen auch die Phasendiagramme eine qualitative Analyse der Räuber-Beute-Beziehungen; insbesondere wenn sie abstrakter oder mathematisch präziser erfolgen soll.
Alle Modelle, die hier vorgestellt wurden oder in der Praxis verwendet werden, starten immer mit vereinfachten Annahmen. Ggf. müssen sie erweitert und angepasst werden, um eine konkrete Situation adäquat beschreiben zu können. So wurde etwa beim exponentiellem Wachstum angenommen, dass immer genug Ressourcen zur Vermehrung zur Verfügung stehen. Eine Erweiterung führte zu logistischem Wachstum, bei dem die intraspezifische Konkurrenz um begrenzte Ressourcen mit einbezogen wurde. Ebenso können hier die Lotka-Volterra-Gleichungen erweitert werden, um diese intraspezifische Konkurrenz zu berücksichtigen. Diese erweiterten Gleichungen sind komplizierter zu analysieren, können aber tatsächliche Situationen besser modellieren (Wirsching, 2006).