Logistisches Wachstum
(Verhulst, 1847)
In der Natur tritt exponentielles Wachstum nie auf, da es offenbar keine Wachstumsprozesse geben kann, die immer weiterlaufen und somit beliebig viele Individuen erzeugen. Bei Experimenten, wie etwa zum Bakterienwachstum, sieht man, dass sich auf eine anfangs exponentiell beginnende Wachstumsphase meist eine Abflachung in der Populationszahl zeigt.
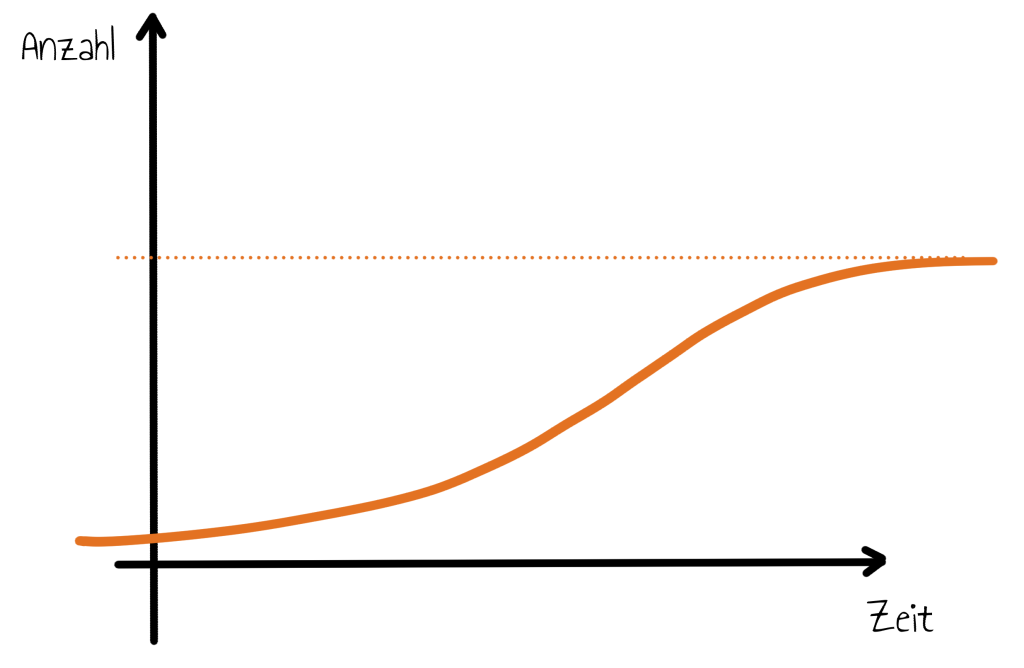
Diese S-förmigen Kurven widersprechen der Annahme, dass Individuen sich unabhängig voneinander fortpflanzen, und sind deswegen sehr viel realistischer. Konkret soll es hier um dichteabhängiges Wachstum gehen, das genau dies beschreibt: Das Wachstum ist langsamer, wenn mehr Individuen vorhanden sind.
Gründe dafür können vielzählig sein und hängen von der konkreten Situation ab: Hasen in einem Waldstück haben nur eine begrenzte Menge an Nahrung; Vögel in demselben Wald nur eine begrenzte Zahl an Nistplätzen. In allen Fällen nähert sich die Populationsgröße $N(t)$ einer Populationsobergrenze $N_{max}$ an und je näher sie dieser Grenze kommt, desto langsamer nimmt die Population zu.
In Szene 1: Hausaufgabenbearbeitung der Modellierungsaufgabe experimentiert Hannah mit einer Simulation zum Bakterienwachstum, um diesen Unterschied von logistischem zu exponentiellem Wachstum herauszuarbeiten. Zuvor hatte sie exponentielles Wachstum als Modell für vorgegebene Daten gefunden.
Das Arbeitsblatt aus dem Video: Download
Die von Hannah verwendete Simulation ist eine leichte Variation der Folgenden:
Anleitung: Mit den Schiebereglern die Anzahl der Bakterien zu Beginn $N_0$ und die Vermehrungsrate $\alpha$ einstellen. Mit dem “Start”-Knopf die Simulation beginnen. Mit dem dann erscheinenden “Stop”-Knopf die Simulation wieder beenden.
Im Gegensatz zum exponentiellen Wachstum zuvor ist die Ableitung der Population $\dot{N}$ nun nicht nur proportional zur Anzahl $N$ selbst, sondern auch zu $N_{max} - N$. Zusammen mit einem Proportionalitätsfaktor $\alpha$, der erneut die Wachstumsrate beschreiben soll, sieht die Differentialgleichung dieses Prozesses hier wie folgt aus:
\[\dot{N} = \alpha\cdot N\cdot (N_{max} - N)\]
Bezeichnet $N_0$ wieder die Populationsgröße zum Beobachtungsbeginn, so lautet die Lösung dieser Differentialgleichung
\[N(t) = N_0\cdot N_{max}\cdot\frac{1}{N_0 + e^{-\alpha N_{max} t}\cdot \left(N_{max} - N_0\right)}\]
Anleitung: Mit den Schiebereglern die Wachstumsrate $\alpha$, die Startanzahl $N_0$ und die Kapazitätsgrenze $N_{max}$ der logistischen Funktion einstellen.
Diese Funktion wird in der Mathematik auch als logistische Funktion bezeichnet und der Prozess ist, neben dichteabhängigem Wachstum, auch als logistisches Wachstum bekannt. (Der Name kommt dabei wohl vom griechischem “logistikós” und wurde von Pierre François Verhulst eingeführt (1847). Die Gründe für die Wahl dieser Bezeichnung sind aber nicht bekannt.)
So wie der Proportionalitätsfaktor $\alpha$ alle Einflussfaktoren zusammenfasst, die die Wachstumsrate an sich beschreiben, hängt die Maximalzahl $N_{max}$ von verschiedensten Einflüssen ab: Etwa den oben bereits erwähnten Nahrungsvorkommnissen und Nistmöglichkeiten, aber auch z.B. von der intraspezifischen Konkurrenz. Da die Differentialgleichung an sich sehr simpel ist und die tatsächlichen Einflussfaktoren in den Konstanten $\alpha$ und $N_0$ versteckt sind, kann diese Gleichung für viele Prozesse, in denen eine Art Sättigung eintritt, verwendet werden.
Ein weiterer Effekt ist in folgendem Ausschnitt aus Szene 1: Hausaufgabenbearbeitung der Modellierungsaufgabe zu sehen. Hannah modelliert basierend auf einer kleinen Zahl von Datenpunkten einen Wachstumsprozess und kommt anfangs zum Ergebnis, dass er exponentiell ist. Erst mit mehr Datenpunkten erkennt sie, dass dieser logistisch ist, wie am Anfang dieser Seite gezeigt.
Was qualitativ an Experimenten und Aufgaben zu sehen ist – dass so ein Wachstumsprozess anfangs exponentiell aussieht – kann auch präzisiert werden: Ist $N_0$ sehr viel kleiner als $N_{max}$, so kann es im Funktionsterm an zwei Stellen ignoriert, sprich als Null angesehen werden. So mit ergibt sich für kleines $N_0$, dass
\[\begin{align*}N(t) &= N_0\cdot N_{max}\cdot\frac{1}{N_0 + e^{-\alpha N_{max} t}\cdot \left(N_{max} - N_0\right)}\\ &\approx N_0\cdot N_{max}\cdot\frac{1}{0 + e^{-\alpha N_{max} t}\cdot \left(N_{max} - 0\right)}\\ &=N_0\cdot N_{max}\cdot\frac{1}{e^{-\alpha N_{max} t}\cdot N_{max}}\\ &=N_0\cdot e^{\alpha N_{max} t}.\end{align*}\]In der Anfangsphase verhält sich logistisches Wachstum also tatsächlich ungefähr so wie exponentielles Wachstum mit Wachstumsrate $\alpha N_{max}$.