Einführung in Differentialgleichungen
(Drossel & Schwabl,1992; Wirsching, 2006)
Die Effekte der biotischen und abiotischen Einflussfaktoren auf Ökosysteme, die im vorherigen Abschnitt vorgestellt wurden, lassen sich zum großen Teil über sogenannte Differentialgleichungen beschreiben. Diese sollen nun kurz abstrakt mathematisch eingeführt werden, bevor sie auf konkrete Beispiele angewandt werden.
Eine Funktion $f:X\to Y$ beschreibt im Allgemeinen eine beliebige Zuordnung von Elementen der Menge $X$ zu Elementen der Menge $Y$. Etwa die Zuordnung
- eines Menschen zu einem Namen,
- eines Automodells zu der Menge der möglichen Felgen,
- einer Sportart zur Anzahl an Spielern pro Team oder
- einer Menge von Äpfeln mit einem bestimmten Gewicht zu ihrem Preis.
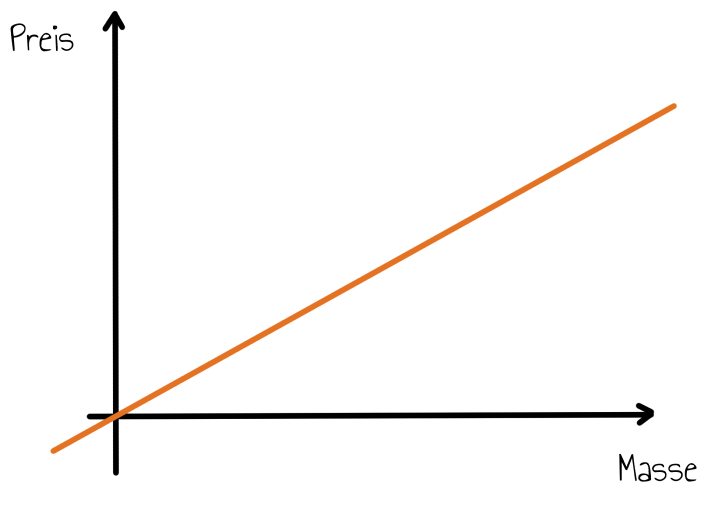
Im letzten Beispiel der Liste obigen Liste haben Menschen eine recht genaue Vorstellung davon, wie sich der Preis von Äpfel verhalten soll: Der Preis $p$ in Abhängigkeit von der Masse $m$ soll linear wachsen. Wenn die Äpfel doppelt so viel wiegen, sollen sie auch doppelt so viel kosten. Es soll also ein Zusammenhang der Form
\[p = \alpha m\]
bestehen, wobei $\alpha$ eine Zahl ist, die den Preis pro Masseneinheit (also etwa $\text{€}$ pro $\text{kg}$) angibt.
Nun lassen sich viele funktionale Zusammenhänge schwierig oder gar nicht direkt beschreiben. Aber sie lassen sich sehr wohl beschreiben, indem man die Veränderungen der vorkommenden Größen miteinander vergleicht. Gleichungen, die solche Veränderungen beschreiben, nennt man Differentialgleichungen. (Hierbei kommt “Differential” vom lateinischen Begriff für “Unterschied”.)
Für diese wird die Ableitung der Funktionen verwendet. Die Ableitung $f’$ einer Funktion $f$ beschreibt die Steigung in einem beliebigen Punkt, sie wird manchmal auch als momentane Änderungsrate bezeichnet. Sie gibt an, wie stark die Funktion an einer bestimmten Stelle zu- oder abnimmt. Dafür wird dort die Tangente angelegt und deren Steigung $\frac{dy}{dx}$ über ein Steigungsdreieck bestimmt.
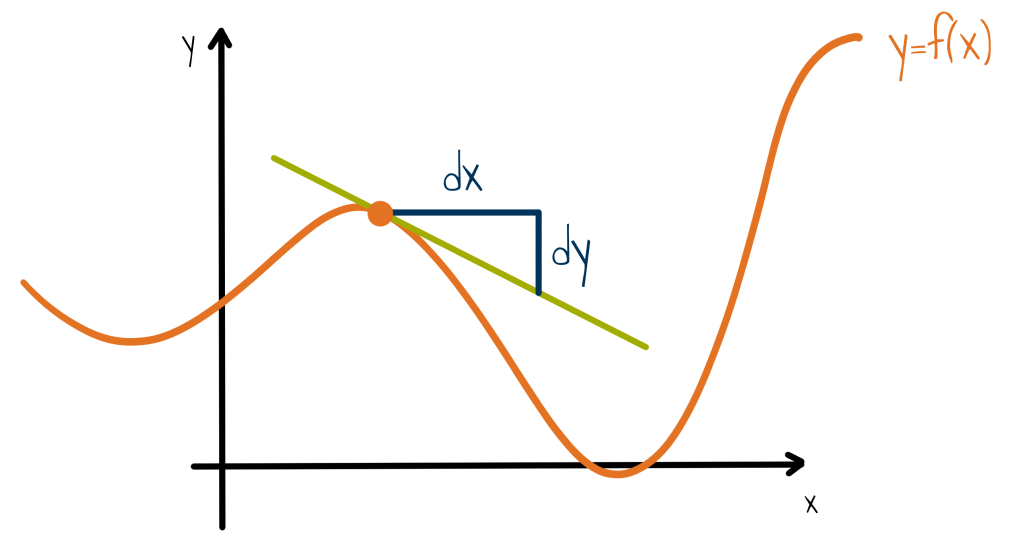
Eine detaillierte Einführung in dieses Thema findet sich im Modul Lehren und Lernen mit Digitalen Medien - Didaktische Prinzipien - Sinus, Cosinus & deren Ableitung.
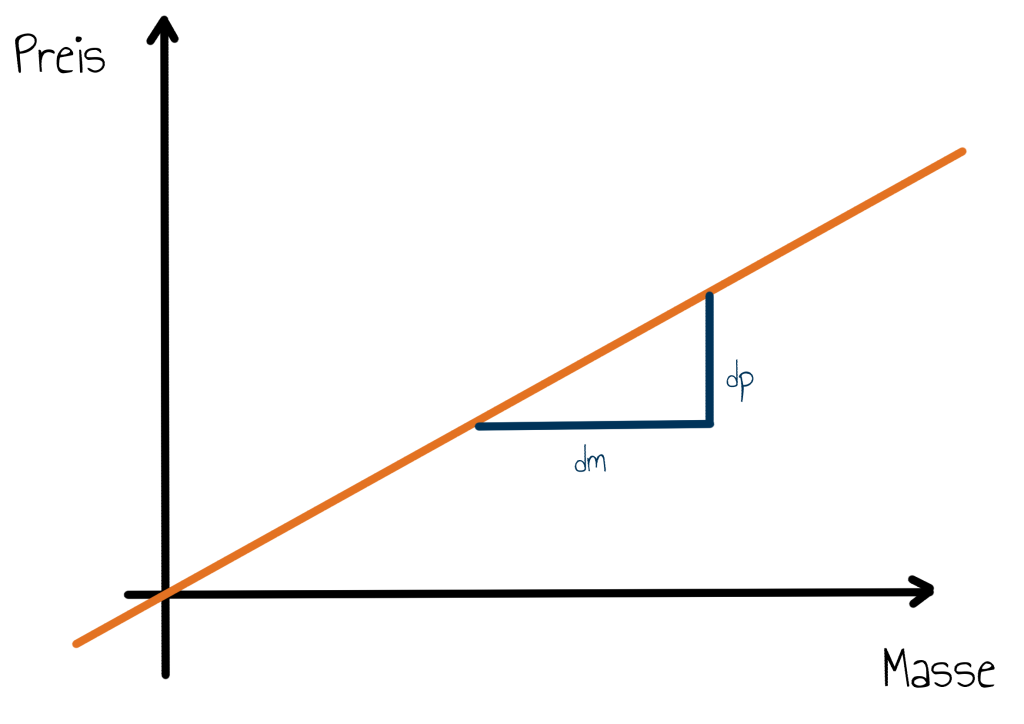
Mit dem Begriff der Ableitung lässt sich etwa das oben genannte Beispiel des Apfelpreises dadurch beschreiben, dass die Änderung des Preises im Vergleich zur Veränderung der Masse konstant sein soll. In Formeln bedeutet das: $p’(m) = \frac{dp}{dm} = \alpha = \text{const}.$
Ableitungen erlauben es, dynamische Prozesse anhand der Änderung einer bestimmten Größe zu beschreiben, anstatt den Wert der Größe direkt ermitteln zu müssen.
Generell stellen sich bei gegebenen Differentialgleichungen meist drei Fragen:
- Gibt es eine Lösung?
- Falls ja, wie kann eine Lösung (bzw. alle Lösungen) bestimmt werden?
- Wie können die Gleichung selbst und ihre Lösung in der Anwendung interpretiert werden?
Die erste Frage zu beantworten ist meist sehr kompliziert. Der Satz von Peano gibt darauf Antwort (Wirsching, 2006). Frage 2 zu beantworten ist meist technisch und unterschiedliche Differentialgleichungen benötigen unterschiedliche Methoden. Hierzu sei ebenfalls auf Wirsching (2006) verwiesen. Im Fokus für diverse Anwendungen in der Biologie steht deshalb die Auseinandersetzung mit Frage 3.
Anwendungsszenarien in der Biologie beschreiben oft Prozesse, die als Wachstum beschrieben werden können. Ein solcher Prozess ist z.B. die Verbreitung von (Wald-)Bränden. Die folgende Simulation stellt einen solchen Brand dar, basierend auf dem Feuerverbreitungsmodell von Drossel und Schwabl (1992).
Anleitung: Mit einem Mausklick im grünen Quadrat “Brandherde” verteilen. Anschließend mit dem “Start”-Knopf die Simulation starten. Der “Zurück”-Knopf setzt alles wieder auf Anfang zurück.
In dieser Simulation gibt es keinen Wind – das Feuer breitet sich in alle Richtungen gleich aus – und es wachsen keine Bäume nach. In diesem Fall erreicht das Feuer am Rand der bestehenden Fläche nur die freie Fläche in der näheren Umgebung; etwa durch Funkenflug. Insbesondere ist es egal, wie weit so ein brennender Baum von der Mitte der bereits verbrannten Fläche entfernt ist.
Wird diese Fläche zu einem Zeitpunkt grob als kreisförmig mit Radius $r$ angenommen, so besagt die Überlegung im letzten Absatz, dass die zeitliche Veränderung des Radius konstant ist. In Zeichen also
\[r’(t) = \omega,\]
wobei $\omega$ die Wachstumsrate bezeichnen soll. Für solche zeitabhängigen Prozesse wird üblicherweise eine spezielle Notation verwendet: Anstatt $r’(t)$ schreibt man kurz $\dot{r}$ und jede Größe, deren Ableitung mit einem Punkt geschrieben wird, wird auch immer implizit als zeitabhängig aufgefasst.
Wie oben beim Apfelbeispiel, führt diese Differentialgleichung zu einem linearen Modell für den Radius der verbrannten Fläche:
\[r(t)= \omega\cdot t + r_0.\]
Hier beschreibt $r_0$ den Radius zu Beginn der Beobachtung. Die verbrannte Fläche $A$ selbst wächst allerdings quadratisch mit der Zeit, denn
\[A(t) = \pi\cdot \left(r(t)\right)^2 = \pi\omega^2\cdot t^2 + 2\pi\omega r_0\cdot t + \pi r_0^2.\]
Dies passt auch zum Graphen, der in der Simulation oben gegeben ist. Allerdings flacht dieser gegen Ende hin ab, da die dem Feuer zur Verfügung stehende Fläche gegen Null geht. Diese Idee wird im Abschnitt zum logistischen Wachstum noch einmal aufgegriffen.