Grundlagen
Manche Lernende können problemlos ableiten, wissen jedoch nicht, wozu es gut ist. Sie stellen sich die Frage: “Was sagt mir mein Ableitungswert an einer bestimmen Stelle meines Funktionsgraphen?”
Zunächst ein Beispiel: Ein Auto fährt von einem Ort $A$ zu einem Ort $B$. Das Auto hatte zum Startzeitpunkt am Ort $A$ einen Kilometerstand von $f(x_0) = 3000\,\mathrm{km}$, wobei der Start um $x_0 = 10\negthinspace :\negthinspace 00$ morgens war. Um $x_0+\Delta x = 11\negthinspace :\negthinspace 30$ erreichen es Ort $B$, wobei der Kilometerstand nun bei $f(x_0+\Delta x) = 3100\,\mathrm{km}$ liegt.
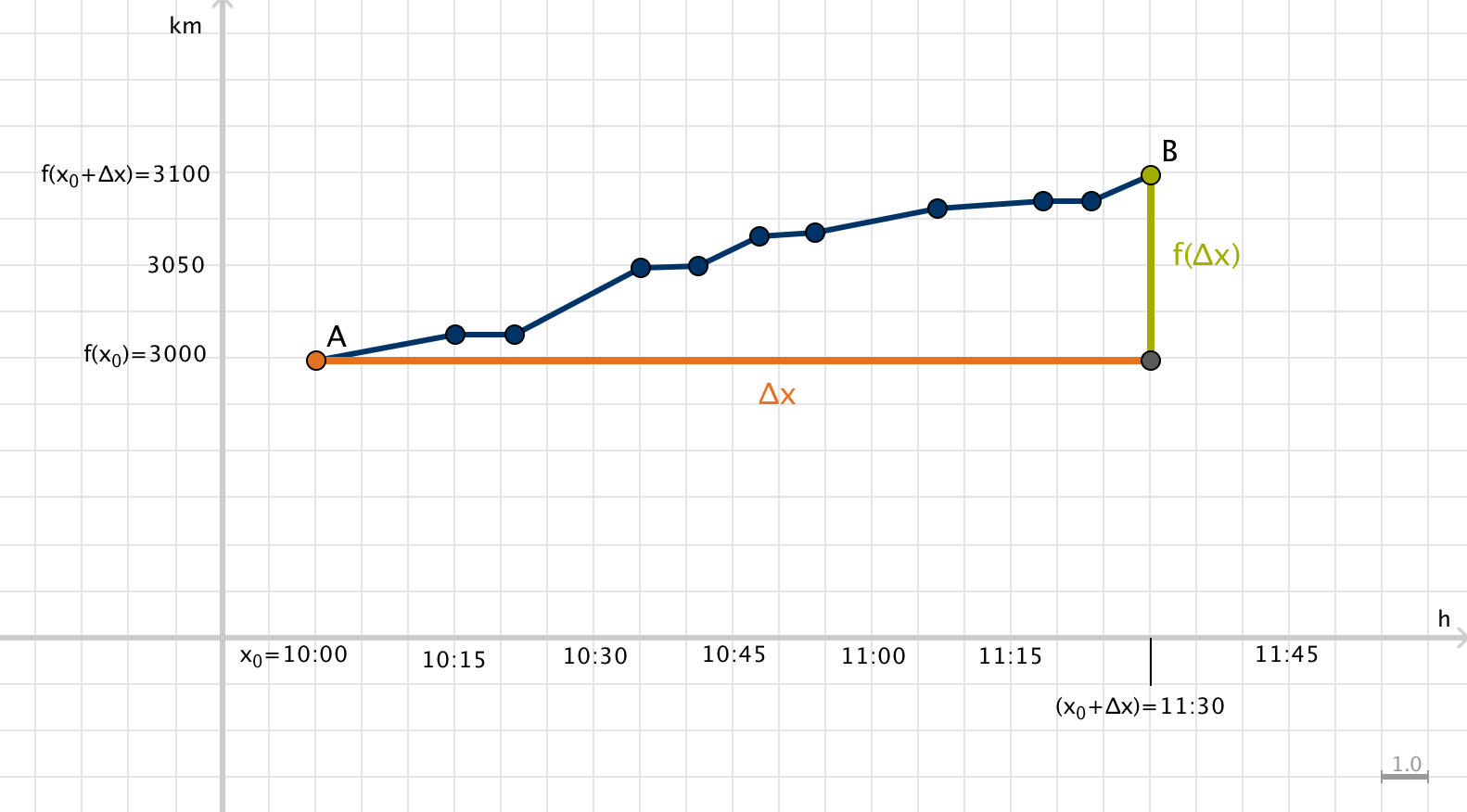
Somit hat das Auto in $1,5$ Stunden $100\,\mathrm{km}$ zurückgelegt. Die Durchschnittsgeschwindigkeit betrug also $v=\frac{ f(x_0+\Delta x)-f(x_0)}{(x_0+\Delta x)-x_0}=\frac{100\,\mathrm{km}}{1,5\,\mathrm{h}}=66,6 \frac{\mathrm{km}}{\mathrm{h}}$, was in der nachfolgenden interaktiven Visualisierung nochmals betrachtet wird. Dies ist die Steigung der Sekante durch die beiden Punkte $ x_0$ und $ (x_0+\Delta x)$ der Funktion.
Anleitung: Den Punkt $B$ nach oben oder unten bewegen und damit die zurückgelegte Strecke in den letzten paar Minuten der Fahrt vergrößern oder verringern.
An der Zeichnung kann die Geschwindigkeit zu einem bestimmten Zeitpunkt, zum Beispiel 10:30 Uhr, leicht herausgefunden werden . Für $ x_0$ wird 10:30 Uhr gewählt. Ein zweiter Punkt auf der Funktion wird $x$ genannt. Dieser wird möglichst nahe an $ x_0$ gelegt. Wenn dann $x$ gegen $x_0$ läuft, so folgt eine Tangente im Punkt $ (x_0, f(x_0))$. Wird der Sachverhalt als Term festgehalten so folgt:
\[f’(x_0) = \lim_{x\rightarrow x_0}\frac{f(x)-f(x_0)}{x-x_0}\]
Durch Ersetzten von $h=x-x_0$, folgt die $h$-Methode, welche aus der Schule bekannt ist.
Die h-Methode
Durch die $h$-Methode kann die Ableitung einer Funktion am Punkt $x_0$ berechnet werden:
\[f’(x_0)=\lim_{h\rightarrow 0}\frac{f(x_0+h)-f(x_0)}{h}\]
Der Differenzenquotient, der auf der rechten Seite betrachtet wird, ist identisch zu dem der gewöhnlichen Definition, wenn man $h = x-x_0$ setzt:
\[\frac{f(x)-f(x_0)}{x-x_0} = \frac{f(x - x_0 + x_0)-f(x_0)}{x-x_0} = \frac{f(x_0+h)-f(x_0)}{h}\]
Allerdings sind in der Praxis manche Ableitungen mit der h-Methode leichter auszurechnen. Das wird z. B. auf der nächsten Seite beim Sinus ersichtlich. Außerdem ist es für Lernende oft einfacher, die Formulierung der h-Methode zu verstehen, da hier das $h$ direkt den Abstand zwischen $x$ und $x_0$ beschreibt.
Weitere Informationen zu den trigonometrischen Funktionen finden sie in (Korntreff, 2017).