Dichte
(Vamvakoussi & Vosniadou, 2010)
Die natürlichen Zahlen zeichnen sich unter anderem dadurch aus, dass jede Zahl einen eindeutigen Nachfolger in den natürlichen Zahlen besitzt. Dies erlaubt insbesondere fundamentale Beweisstrategien wie die Vollständige Induktion. Hierbei werden natürliche Zahlen als Ordinalzahlen aufgefasst: Diese ermöglichen es, die Reihenfolge von Dingen zu beschreiben. Ist ein Objekt das $n$-te, so ist das nächste das $(n+1)$-te.

Darüber hinaus erlauben die natürlichen Zahlen auch die Größe von Mengen zu beschreiben; sie dienen somit als Kardinalzahlen: Für zwei Mengen mit $n$ und $m$ Elementen ist es immer eindeutig, ob entweder $n<m$, $n=m$ oder $n>m$ gilt.

Das Besondere an den natürlichen Zahlen ist hierbei, dass die ordinalen und kardinalen Aspekte verträglich miteinander sind. Das bedeutet: Sind zwei natürliche Zahlen $a,b\in\mathbb{N}$ mit $a\leq b$ gegeben, dann gilt für jede weitere Zahl $c\in\mathbb{N}$, dass $a + c \leq b + c$. Diese Eigenschaft geht beim Übergang zu den Bruchzahlen verloren.
Ein zentrales Ergebnis der ersten Studiensemester ist, dass die rationalen Zahlen abzählbar sind. Sie können mithilfe der natürlichen Zahlen durchnummeriert werden. Die typische Methode für positive Brüche sieht wie folgt aus: Brüche werden in eine Tabelle eingetragen, deren Spalten die Zähler sind und die Zeilen die Nenner. So steht in der achten Spalte und fünften Zeile etwa der Bruch $\frac{8}{5}$.
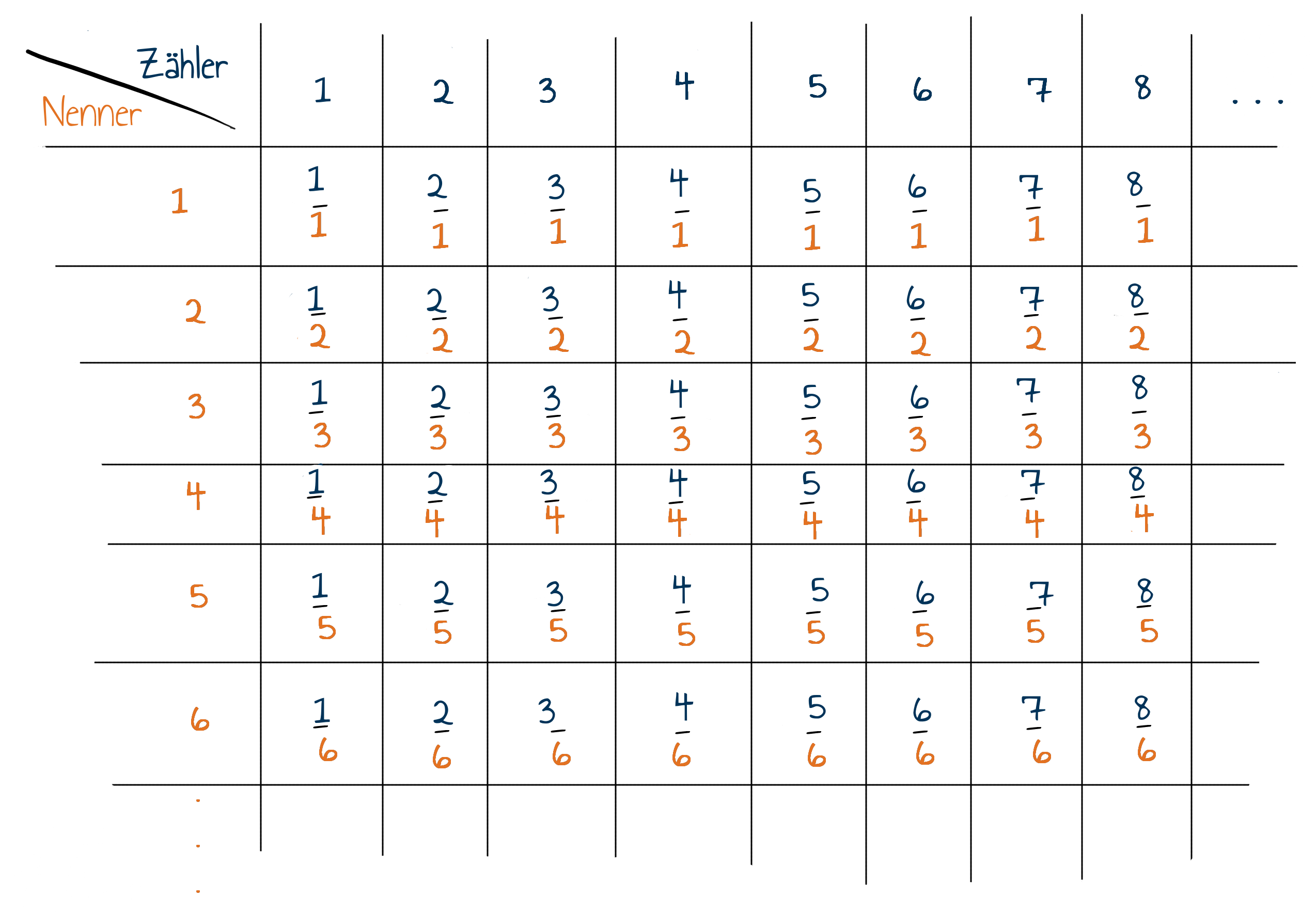
Anschließend wird oben links beginnend im Zickzack durch die Tabelle gelaufen…

sodass die folgende Folge rationaler Zahlen entsteht:
\[\frac{1}{1}, \frac{2}{1}, \frac{1}{2}, \frac{1}{3}, \frac{2}{2}, \frac{3}{1}, \frac{4}{1}, \frac{3}{2}, \frac{2}{3}, \frac{1}{4}, \frac{1}{5}, \frac{2}{4}, \frac{3}{3}, …\]
So wird jeder Eintrag in der Tabelle einmal erreicht und jeder positive Bruch taucht auch einmal in der Tabelle auf. Um das Argument korrekt zu Ende zu führen, benötigt man noch
- eine Möglichkeit nicht-positive ganze Zahlen in der Liste der Zähler mit aufzuführen, z.B. via $0,1,-1,2,-2,3,-3,…$, und
- den Hinweis, dass wiederholt auftauchende Bruchzahlen übersprungen werden sollen.
Dieses Ergebnis bedeutet, dass auch Bruchzahlen als ordinal angesehen werden können, denn bei Bedarf können sie angeordnet werden. Allerdings ist diese Sichtweise nicht mit der Größe der Bruchzahlen – ihrem kardinalen Aspekt – verträglich. Zwischen je zwei Bruchzahlen liegt immer eine weitere. Diese Eigenschaft wird Dichte genannt. Der Beweis dafür ist denkbar einfach und gibt die dazwischenliegende Bruchzahl explizit an: Seien die beiden Bruchzahlen durch die Brüche $\frac{a}{b}$ und $\frac{c}{d}$ gegeben. Dann liegt ihr Durchschnitt $\frac{1}{2}\left(\frac{a}{b} + \frac{c}{d}\right) = \frac{ad + bc}{2bd}$ zwischen ihnen und ist wieder eine Bruchzahl.
Insbesondere heißt das, dass es, egal wie die rationalen Zahlen durchnummeriert werden, immer eine Bruchzahl zwischen der $i$-ten und der $(i+1)$-ten gibt. Das Konzept, dass der Nachfolger die nächstgrößere Zahl ist und umgekehrt, ist für rationale Zahlen also nicht mehr gültig.
Das Festhalten an dieser Vorstellung ist allerdings so stark, dass Lernende – selbst wenn sie wissen, dass zwischen zwei Bruchzahlen weitere liegen und evtl. sogar den obigen Beweis mittels des Durchschnittswerts kennen und verstehen – bei Brüchen mit gleichem Nenner und aufeinanderfolgenden Zählern – wie z.B. $\frac{3}{7}$ und $\frac{4}{7}$ – trotzdem der Meinung sind, dass kein Bruch dazwischen existiert (Vamvakoussi & Vosniadou, 2010).