Konsequenzen für den Unterricht
(Gerster, 1994; Krauthausen & Scherer, 2007; Kuhnke, 2013; Kuntze, 2013; Laakmann, 2013; Wittmann, 1981; Zech, 2002)
Mentale Bilder
Selbst wenn die Struktur des mathematischen Sachverhaltes adäquat in einem Arbeitsmittel repräsentiert ist, dann gibt es nach Krauthausen & Scherer (2007) keinen direkten und zwingenden Weg vom Anschauen des Arbeitsmittels zur gewünschten Verinnerlichung des mathematischen Begriffs, da es sich hierbei um einen konstruktiven Akt des lernenden Individuums handelt.
Es gibt keine automatische Verinnerlichung mathematischer Ideen, Strukturen oder Begriffe, nur weil mit Arbeitsmitteln konkret umgegangen wird. Dies ist unabhängig von der Qualität der Arbeitsmittel im Hinblick auf die Repräsentanz dieser Strukturen im Material. Überinterpretation und formalistische Handhabung des EIS-Prinzips können dazu führen, dass das Arbeiten am konkreten Material zum Selbstzweck wird und sich verselbstständigt. Handlungsaufforderungen können dann sehr aufwendig werden, so dass Lernende unter solchen Umständen das Rechnen mit konkretem Material als schwierig einstufen. Stattdessen greifen sie auf andere Methoden zurück, die durchaus fehleranfälliger sein können. Eine wünschenswerte Einstellung der Lernenden gegenüber Arbeitsmitteln und Veranschaulichungen kann sich nur dann entwickeln, wenn die eingesetzten Materialien die Nutzung effektiver Strategien auch wirklich nahelegen.
Ziel des Einsatzes von Arbeitsmitteln und Veranschaulichungen ist nach Gerster (1994) nicht eine schlichte Vereinfachung der Zugänge zu mathematischen Sachverhalten, sondern die Konstruktion und der Ausbau klarer, tragfähiger mentaler Vorstellungsbilder, an denen die arithmetischen Operationen in der Vorstellung ausgeführt und die Rechenergebnisse abgelesen werden können. Der Aufbau dieser mentalen Strukturen – wie die Fähigkeit des mentalen Operierens – braucht sowohl Zeit als auch planvolle AKtivitäten, die dafür förderlich sind.
Vielfältige Darstellungen als Lernhilfe
Laut Kuntze (2013) ist wesentlich
-
Anregungen zum Nutzen vielfältiger Darstellungen zielgruppengerecht zu gestalten:
Zielgruppengerecht bedeutet beispielsweise für Kindergarten und Grundschule, enaktive und bildliche Zugänge anzubieten, und diese zu verknüpfen. In den Sekundarstufen, beispielsweise im Gymnasialunterricht bedeutet eine zielgruppengerechte Ausrichtung in erster Linie auch, dass Aufgaben so gestellt werden, dass Lernende als aktive Wissenskonstrukteure ernst genommen werden. So zeichnet sich eine geeignete Fragestellung dadurch aus, dass altersgruppengerecht auch über die Rolle des Darstellungswechsels reflektiert werden soll. -
Verknüpfungen zu Vorerfahrungen, Vorwissen und Vorstellungen der Schülerinnen und Schüler anzuregen:
Sind Darstellungen und diesbezügliche Darstellungswechsel für Lernende neu, ist darauf zu achten, dass diese von den Lernenden integriert werden können. Es ist wichtig, die Lernvoraussetzungen der Lernenden zu berücksichtigen, indem verwendete Darstellungen an Vorerfahrungen angeknüpft werden. Dies können Vorerfahrungen mit situativen Kontexten sein, oder Vorerfahrungen mit bestimmten Darstellungsformen, zu denen bereits Wissen aufgebaut wurde. -
Darstellungswechsel als explizite Anregung auffassen, um das dahinterstehende abstraktere mathematische Konzept zu erschließen:
Wird dies nicht berücksichtigt, so besteht die Gefahr, dass aus Sicht der Lernenden verschiedene Darstellungen unverbunden nebeneinander stehen. Zudem können Darstellungswechsel in der Wahrnehmung der Lernenden rezeptähnliche Züge annehmen, die nicht als zielführend erachtet werden. Eine Aufgabe sollte Impulse geben, den Hintergrund eines Darstellungswechsels zu reflektieren. Ziel ist hierbei, die hinter den Darstellungen stehende mathematische Konzepte in den Fokus zu rücken
Umsetzen der Repräsentationsmodi
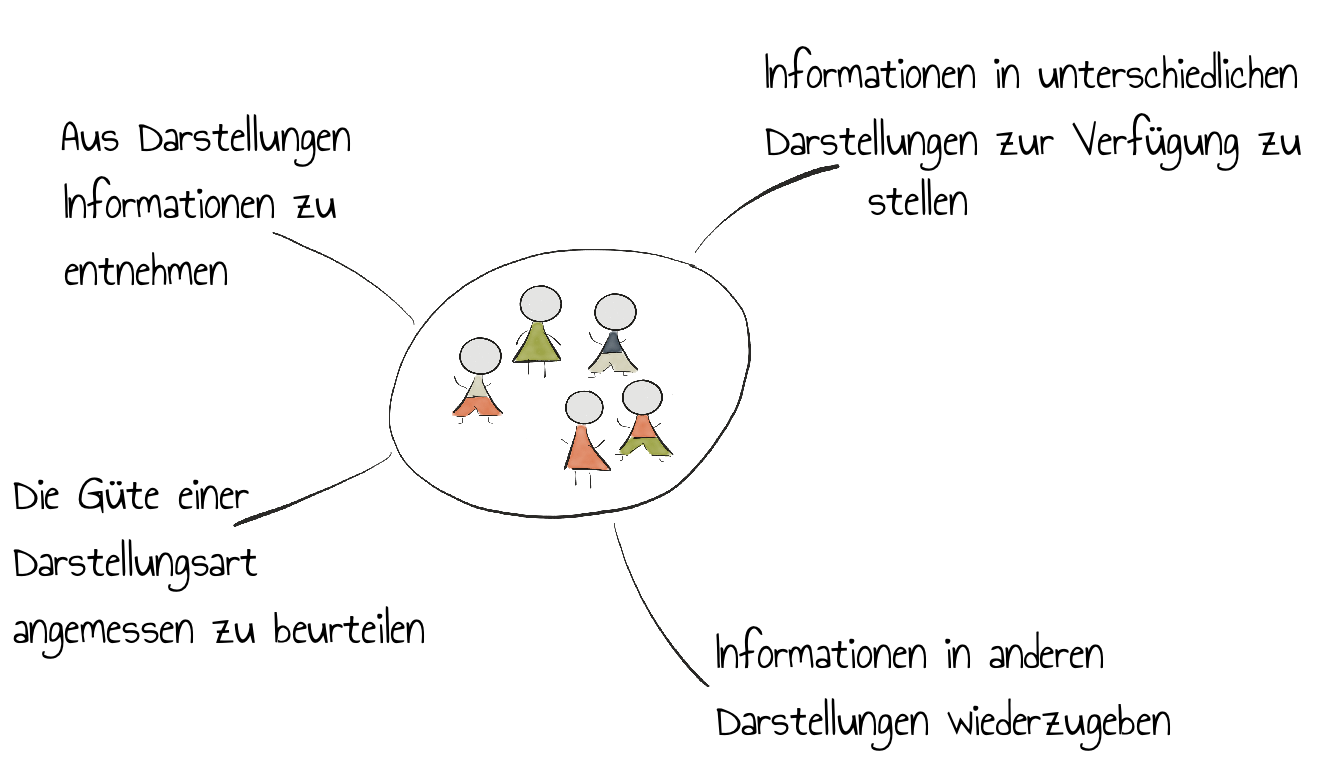
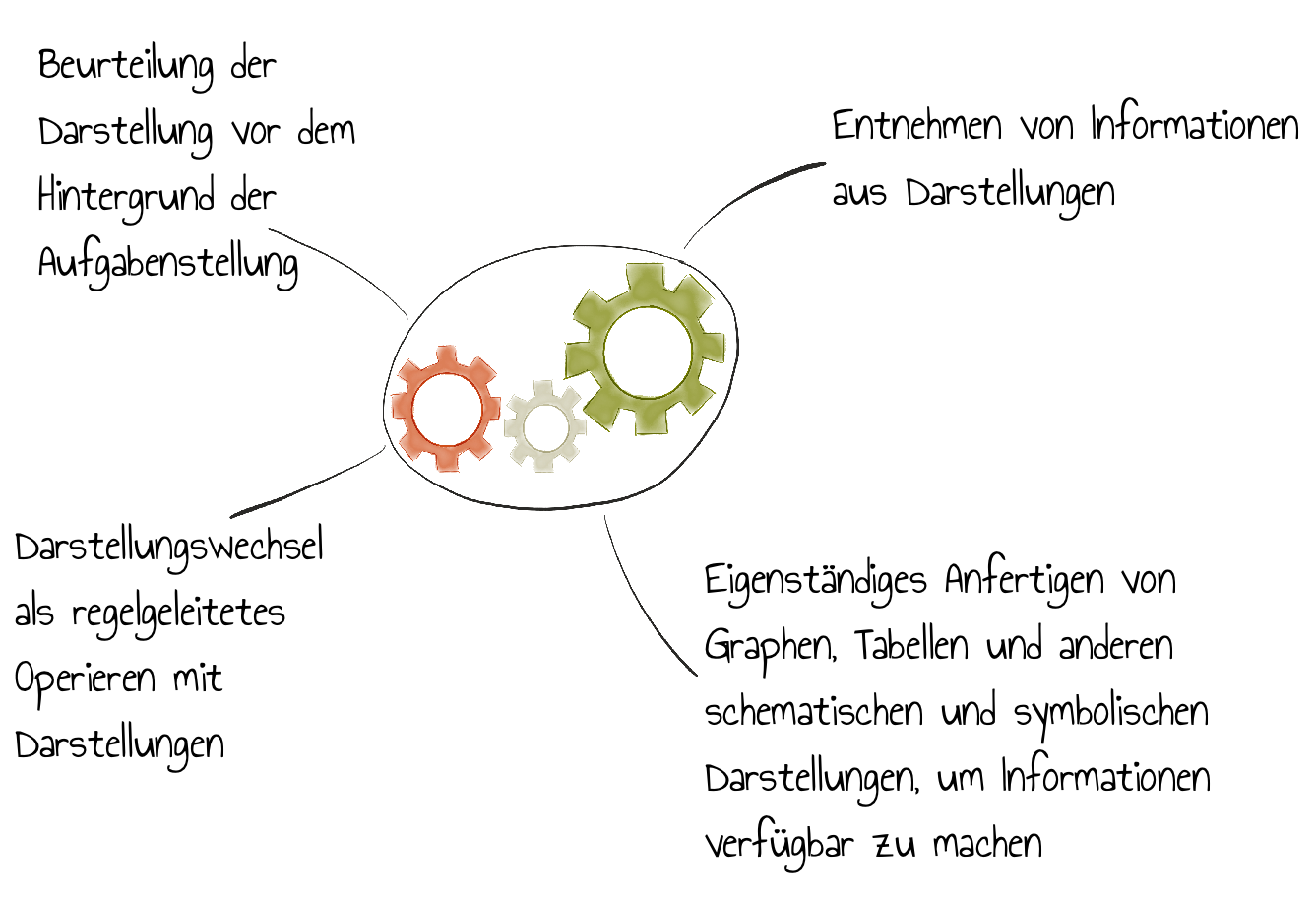
Lernumgebungen müssen nach Laakmann (2013) Schülerinnen und Schülern die Möglichkeit bieten:

Der Umgang mit Darstellungen kann operationalisiert werden durch:
Anwendungsbeispiele
(vgl. Wittmann, 1981)
Enaktive und ikonische Präsentation von Aufgaben:
- Enaktive Problemstellung: Vorführung der Spielregeln
- Ikonische Problemdarstellung: Vorlage einer Plättchenkonfiguration und weitere Umrisse, in die sich die Plättchen ebenfalls legen lassen
Sprachliche Formulierung von Aufgaben:
- Eher schlecht: Wie viele Geraden gibt es durch 2, 3, 4, .. Punkte, wenn nicht mehr als zwei der Punkte kollinear sind?
- Besser: Zeichne drei Punkte, die nicht auf einer Geraden liegen. Wie viele Verbindungsgeraden kann man ziehen? Zeichne einen weiteren Punkt. Wie viele Verbindungsgeraden kann man nun zwischen den vier Punkten zeichnen? Zeichne einen weiteren Punkt.
- Hier wird die Handlungssequenz ersichtlich!
Videobeispiel
In Szene 4: Präsentation der Ergebnisse wird die Arbeit der Gruppen vorgestellt. Damit informieren die Lernenden ihre Klasse über ihre jeweiligen Hilfsmittel und Aufgaben und betonen Vor- und Nachteile dieser.
Überlegen Sie sich, inwiefern die gezeigte Lernumgebung den Anforderungen nach Laakmann (2013) entspricht. Hätte man einzelne Aspekte noch ausführlicher besprechen sollen?