Der Wechsel zwischen den Darstellungsebenen
(Dreher, 2013; Duval, 2006; Friesen & Kuntze, 2017; Friesen, Kuntze & Vogel, 2015; Jörissen & Schmidt-Thieme, 2015; Kuhnke, 2013; Kuntze, 2013; Wittmann, 1981; Zech, 2002)
Der Darstellungswechsel in Teilkompetenzen
Jörissen & Schmidt-Thieme (2015) beschreiben eine Einteilung in – zum Teil als Stufen anzuordnende – Teilkompetenzen (vgl. Duval 2006), die Lernende für den Wechsel von Darstellungen benötigen:
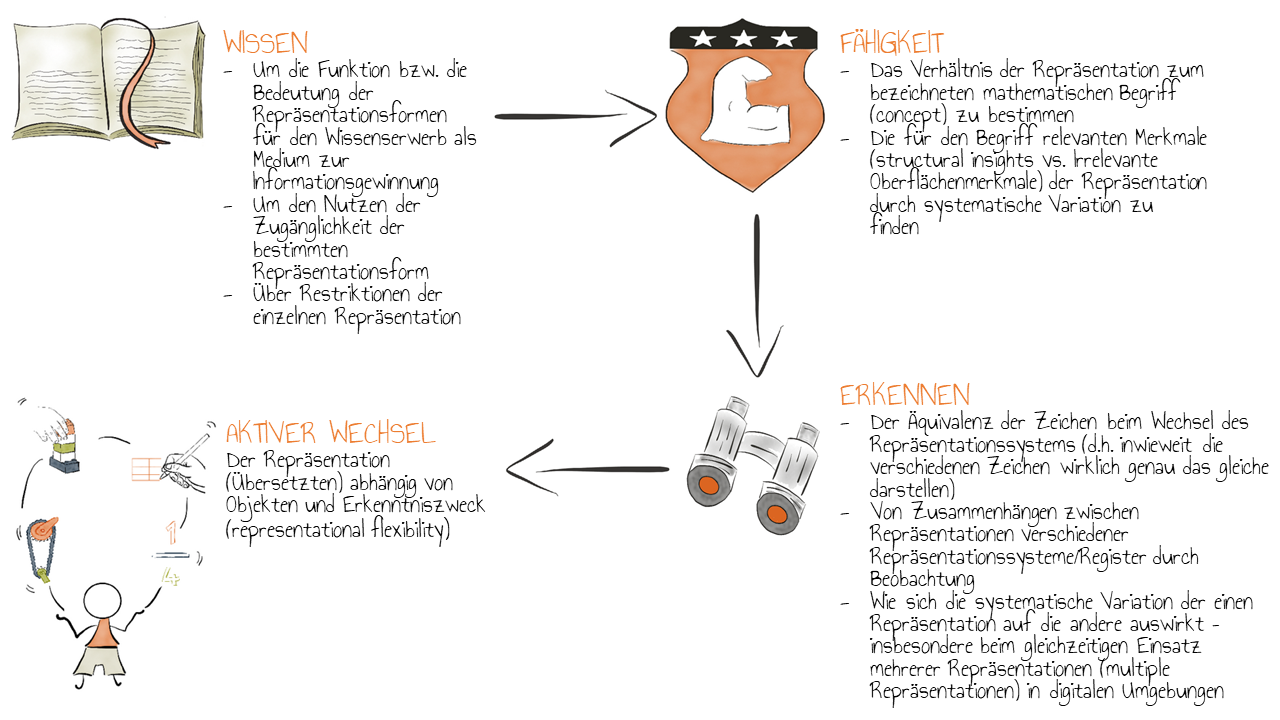
Verschiedene Aspekte des Darstellungswechsels
Es gibt eine Differenzierung zwischen dem sogenannten intramodalen und dem intermodalen Transfer (vgl. Kuntze, 2013). Diese Unterscheidung ist an das EIS-Prinzip nach Bruner (1970) gebunden: ein intermodaler Transfer liegt erst bei dem Wechsel zwischen Darstellungsebenen vor, also beispielsweise zwischen einer enaktiven und einer ikonischen Darstellung. Demgegenüber gilt der Wechsel etwa zwischen Tabelle und Diagramm als intramodaler Transfer, da beide dieser Darstellungsformen der ikonischen Darstellungsebene zugerechnet werden.
Duval (2006) unterscheidet beim Wechseln zwischen Darstellungen sogenannte Treatments und Conversions. Während Treatments Veränderungen von Darstellungen innerhalb einer bestimmten Darstellungsart sind (z.B. Äquivalenzumformungen einer Gleichung), bestehen Conversions in einer Übersetzungsleistung zwischen verschiedenen Darstellungsarten, z.B. der Übersetzung einer algebraischen Gleichung in zwei Funktionsgraphen, für die nach Schnittpunkten gesucht wird.
Duval (2006) stellt fest, dass Treatments meist ein geringeres Anforderungsniveau aufweisen als Conversions. Während Treatments oft algorithmisch abgearbeitet werden können, beziehen sich Conversions auf darstellungsbezogene Aspekte von Begriffswissen, über das Lernende verfügen müssen, um Conversions erfolgreich ausführen zu können. Daher treten beim Nutzen vielfältiger Darstellungen häufig Schwächen von Lernenden im Begriffswissensbereich zu Tage.
Interaktion der Darstellungsformen
Verschiedene Darstellungen zu einem mathematischen Begriff stützen und ergänzen sich nach Kuhnke (2013) gegenseitig. Interaktionen beziehen sich auf ein wechselseitiges Aufeinanderwirken von Darstellungen. Die Fähigkeit, einen Inhalt von einer Darstellung in eine andere zu übertragen, wird gefördert. Wissen, dass in verschiedenen Darstellungsmodi erworben wurde und verfügbar ist, kann leichter behalten werden und die Fähigkeit, Wissen nach Bedarf in die eine oder andere Form zu transponieren, erhöht die Flexibilität und den Erfolg beim Problemlösen.
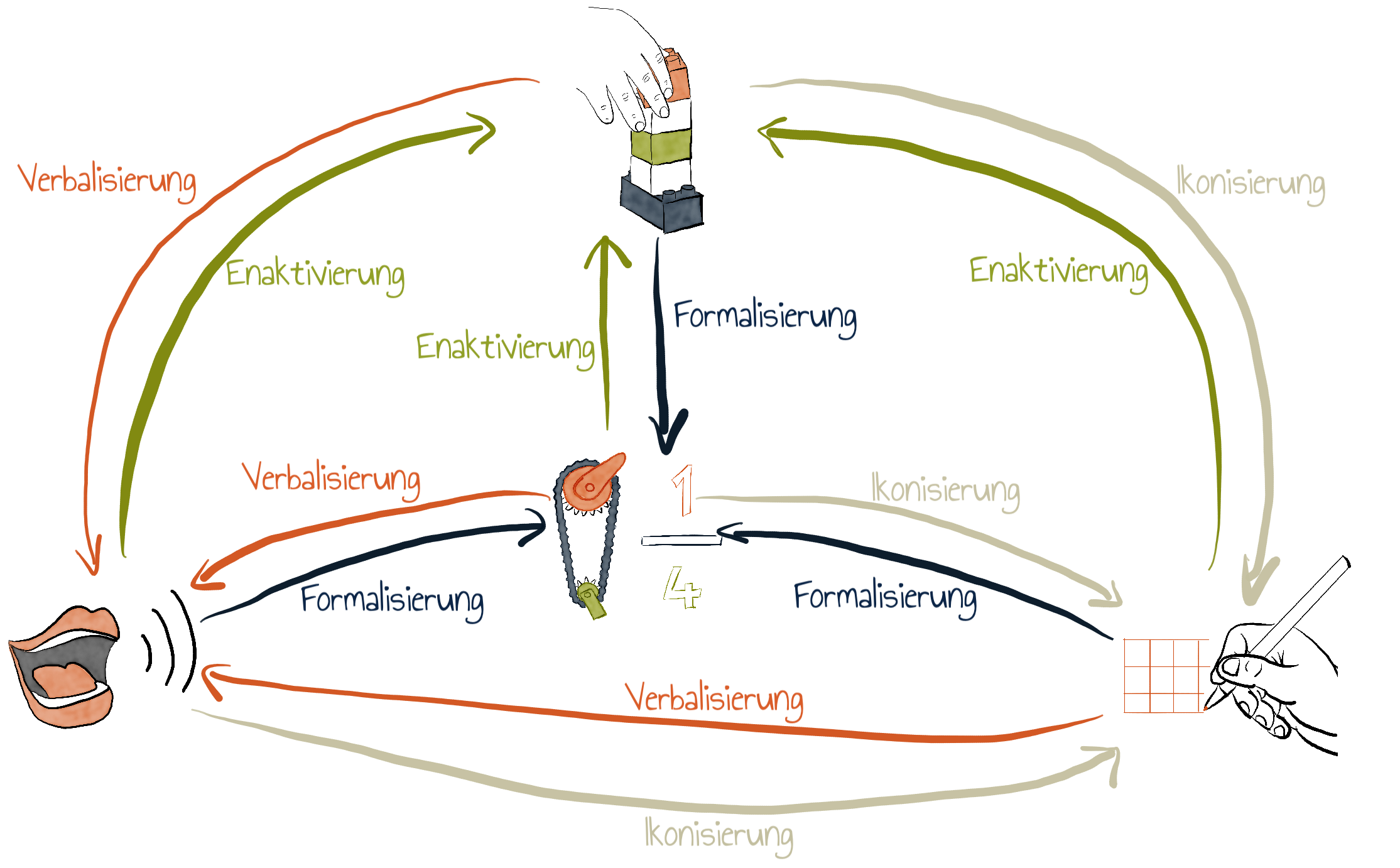 Abbildung: Darstellungsübergänge in Anlehnung an Zech (2002, S. 106)
Abbildung: Darstellungsübergänge in Anlehnung an Zech (2002, S. 106)
Nach Bruner (1970) sollen alle Übergänge zwischen den Darstellungsebenen geübt und verinnerlicht werden. Es soll also nicht nur die Abstraktion, sondern auch die Konkretisierung geübt werden.
Verwendung unterschiedlicher Darstellungen
Die Verwendung vielfältiger Darstellungen im Unterricht ist nach Friesen & Kuntze (2017) eine notwendige Voraussetzung für den Aufbau mathematischen Wissens, erfordert von den Lernenden jedoch auch, zwischen den verschiedenen Darstellungen eines mathematischen Objekts zu wechseln. Solche Darstellungswechsel verlangen von den Lernenden komplexe Denkleistungen und sind auch häufig die Ursache für Verständnisschwierigkeiten. Für Lehrende ist es daher besonders wichtig, potenzielle Lernhürden beim Wechsel von Darstellungen zu erkennen, um die Lernenden unterstützen zu können.
Dreher (2013) kommt zu dem Schluss, dass verschiedene Repräsentationen und Darstellungswechsel angeboten werden sollten. Der Fokus soll aber nicht darauf liegen, maximal viele verschiedene Repräsentationen einzusetzen, da dies nicht automatisch zu einem tieferen Verständnis führt.
Entscheidend für das Verständnis von Lernenden ist nach Friesen, Kuntze & Vogel (2015) nicht das bloße Vorkommen von vielfältigen Darstellungen im Unterricht, sondern der Umgang mit diesen. Lehrende müssen sich der doppelten Rolle von Darstellungen als Lernhilfe und potenzieller Lernhürde bewusst sein, um entsprechend gezielte Unterstützung und geeignete Reflexionsanlässe beim Umgang mit vielfältigen Darstellungen anbieten zu können.
Die insgesamt zwölf Übergänge müssen natürlich nicht in jeder Übung berücksichtigt werden, geben aber Anregungen bei der Erstellung von Aufgaben.
Besonders effektiv ist die gleichzeitige Anwendung von verschiedenen Darstellungsmodi. Beispielsweise kann eine Handlung gleichzeitig verbalisiert werden oder ein Bild kann durch eine Handlung überlagert werden, wie etwa das Nachfahren eines rechtwinkligen Dreiecks. Notieren Sie sich noch ein weiteres Beispiel, wie Sie mehrere Darstellungsmodi gleichzeitig ansprechen könnten. Reflektieren Sie Ihren bisher erlebten Unterricht. Gab es eine solche Übung?