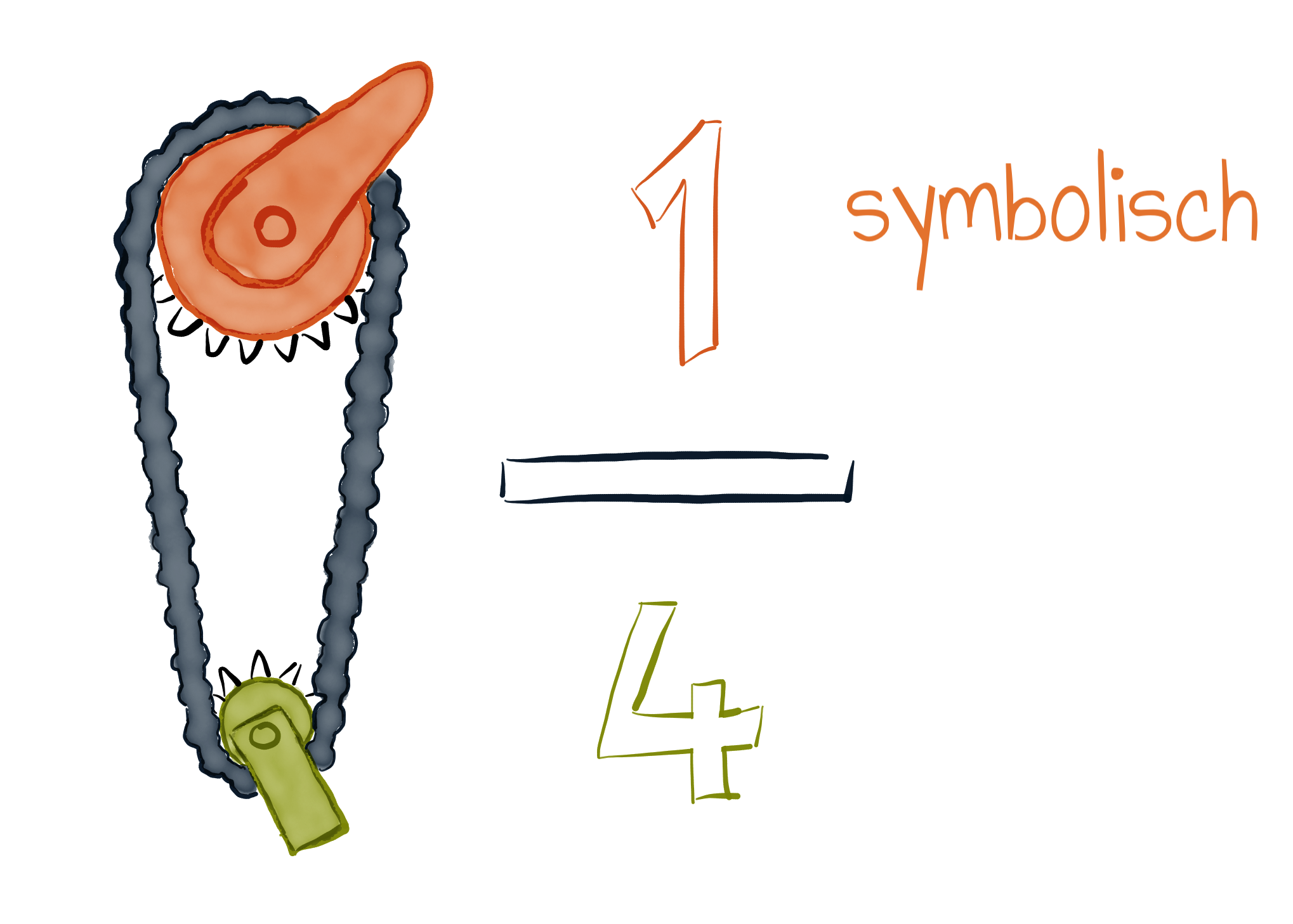Die drei Ebenen
(Dienes, 1971; Fischer, 1984; Kaputt, 1989; Kaufmann & Wessolowski, 2006; Kuhnke, 2013; Laakmann, 2013; Wittmann, 1981 & 1998; Zech, 2002)
Die enaktive Ebene ist im Primarbereich besonders wichtig. Hier spielen auch die „embodiments“ von Dienes (1971) eine Rolle. Dienes Idee beruht auf der Annahme, dass viele unterschiedliche Materialien nötig sind, um beim Kind ein umfassendes Verständnis eines mathematischen Begriffs zu erzeugen. Das Arbeiten mit konkretem Material (Einerwürfel, Zehnerstangen, Hunderterplatten, …) hilft, die abstrakten mathematischen Begriffe einzuführen. Später wird das Arbeiten mit mathematischen Symbolen vom konkreten Material abgelöst.
Videobeispiel
In Szene 1: Entdecken von wertgleichen Brüchen sehen Sie in untenstehendem Ausschnitt, wie Brüche enaktiv dargestellt werden können. Wichtig ist hierbei, dass die Lernenden die Handlung selbst durchführen. Es wird zudem betont, dass es nicht die eine richtige Lösung gibt, sondern unterschiedliche Versionen die Aufgabe erfüllen.
Bildliche Darstellungen haben eine Vermittlungsfunktion zwischen Mathematik (den mathematischen Zeichen und abstrakten Aussagen) und der Realität (Erfahrungswelt der Kinder). Dies ist zurückzuführen auf die amphibische Eigenschaft (vgl. Wittmann, 1998). Bildliche Darstellungen sind semi-konkret, also anwendbar in speziellen Kontexten, und semi-abstrakt, also gültig für eine Reihe von Kontexten. Beispielsweise können Wendeplättchen Personen, Tiere und Gegenstände gleichermaßen darstellen. Dies darf allerdings nicht als den Darstellungen inhärent angesehen werden, sondern muss vielmehr über Interaktionen und Aushandlungsprozesse wahrgenommen werden.
Das Ikonisieren erhält in der Mathematikdidaktik mitunter deshalb besondere Aufmerksamkeit, da es die einzige Möglichkeit darstellt, in Schulbüchern abstrakte Inhalte zu visualisieren. Zudem erlauben Bilder die simultane Erfassung von Handlungsketten sowie die Protokollierung und den Vergleich von Handlungen, die konkret nicht gleichzeitig durchführbar sind.
Beispiele zur Ikonisierung nach Zech (2002):
- Zahlenstrahl, um den Begriff der natürlichen Zahlen besser zu verstehen. Diese Repräsentation verschafft Lernenden einen besseren Einblick in die Ordnungsstruktur der natürlichen Zahlen.
- Baumdiagramm, um verschiedene Alternativen simultan zu erfassen, die auf Handlungsebene (enaktiv) nur nacheinander zu erfahren sind.
- Situationsskizzen, um Handlungen oder Texte in ein verständliches Bild zu übersetzen. Allgemein handelt es sich bei einer Situationsskizze um eine Problemlösungshilfe.
Indem viele Darstellungen bereitgestellt werden, wird den Lernenden die Gelegenheit geboten, Beziehungen zwischen diesen herzustellen. Diese Beziehungen ermöglichen wiederum eine tiefere Einsicht in den mathematischen Begriff (vgl. Kaputt, 1989).
Videobeispiel
In Szene 2: Gruppenarbeit sehen Sie im untenstehenden Ausschnitt, wie eine Gruppe mit einem eBook auf dem Tablet arbeitet. Dieses zeichnet sich vor allem durch ikonische Darstellungen der Brüche aus. Es werden verschiedene Unterteilungen von Pizzen und Kreisen, aber auch Unterteilugen in Rechtecke dargestellt.
Hinweis: Das ALICE eBook gilt generell als enaktives Hilfsmittel, da die Lernenden an vielen Stellen Handlungen mit den Händen nachvollziehen. In diesem Beispiel wird aber explizit auf die ikonische Darstellung Bezug genommen, die im Video zu sehen ist.
Das Gewicht der symbolischen Repräsentationsform liegt nicht im einzelnen Symbol, sondern in der Vereinigung von Symbol und Sprache. Auch die mathematischen Strukturen können als formale Sprache aufgefasst werden, wobei „formal“ bedeutet, dass diese Strukturen sich in verschiedener Weise konkret interpretieren lassen. Nach Kaufmann & Wessolowski (2006) gibt es eine feinere Unterteilung der symbolischen Ebene in mathematisch-symbolisch (2 x 4) und sprachlich-symbolisch (in der Umgangssprache mit oder ohne Kontextbezug: Timo geht zweimal in den Keller und holt jeweils vier Flaschen).
Symbolische Darstellungen zeigen einzelne Aspekte eines Sachverhalts, jedoch bezogen auf das Aussehen mit einer großen Beliebigkeit. Ihre Bedeutung muss vorher vereinbart werden. Symbole weisen in der Regel keine Ähnlichkeit zum dargestellten Gegenstand auf und müssen deshalb gelernt werden.
Mathematische Symbole sind zudem kontextfrei. Sie sind nicht mehr an vorgegebene Ausgangsituationen gebunden, sondern können für alle gleich strukturierten Fälle verwendet werden. Mathematische Symbole werden vor allem für formale Beweise und allgemeine Aussagen benutzt.
Videobeispiel
Im untenstehenden Ausschnitt von Szene 4: Präsentation der Ergebnisse sehen Sie die Arbeit der Gruppe, die klassisch mit Stift und Papier gearbeitet hat. Auf dem Arbeitsblatt sind lediglich die symbolischen Darstellungen der Brüche abgebildet. In der Lösung der Lernenden lässt sich erahnen, dass eine ikonische Hilfszeichnung bei der Bearbeitung verwendet wurde. Der Lösungsweg der Lernenden erstreckt sich also auf verschiedene Ebenen.