Bruners Theorie
(Bruner, 1970; Käpnick, 2014; Reiss & Hammer, 2013; Wittmann, 1981)
Bruner entwickelte Piagets Theorien weiter, insbesondere im Hinblick auf die soziale Umwelt eines Kindes. Für ihn ist Lernen ein Prozess individueller Konzeptbildung, der zitiert nach Käpnick (2014, S.53) durch drei wesentliche Merkmale charakterisiert wird:

Die Denkentwicklung sieht er nicht in Stufen, die zeitlich nacheinander ablaufen, sondern auf Darstellungsebenen, die gleichzeitig angesprochen werden und sich wechselseitig beeinflussen. Die Denkentwicklung nach Bruner wird charakterisiert durch eine immer bessere Koordination zwischen den Repräsentationsebenen, mit denen sich ein Mensch seine Umwelt erschließen kann.
- Enaktive Ebene: Sachverhalte werden durch eigene Handlungen erschlossen. Dominierend vor allem bei jungen Kindern.
- Ikonische Ebene: Verstehen von Sachverhalten durch Bilder oder Graphiken. Dominierend bei Jugendlichen und jungen Erwachsenen.
- Symbolische Ebene: Das Abstrakte steht im Vordergrund. Dominierend bei Jugendlichen und jungen Erwachsenen.
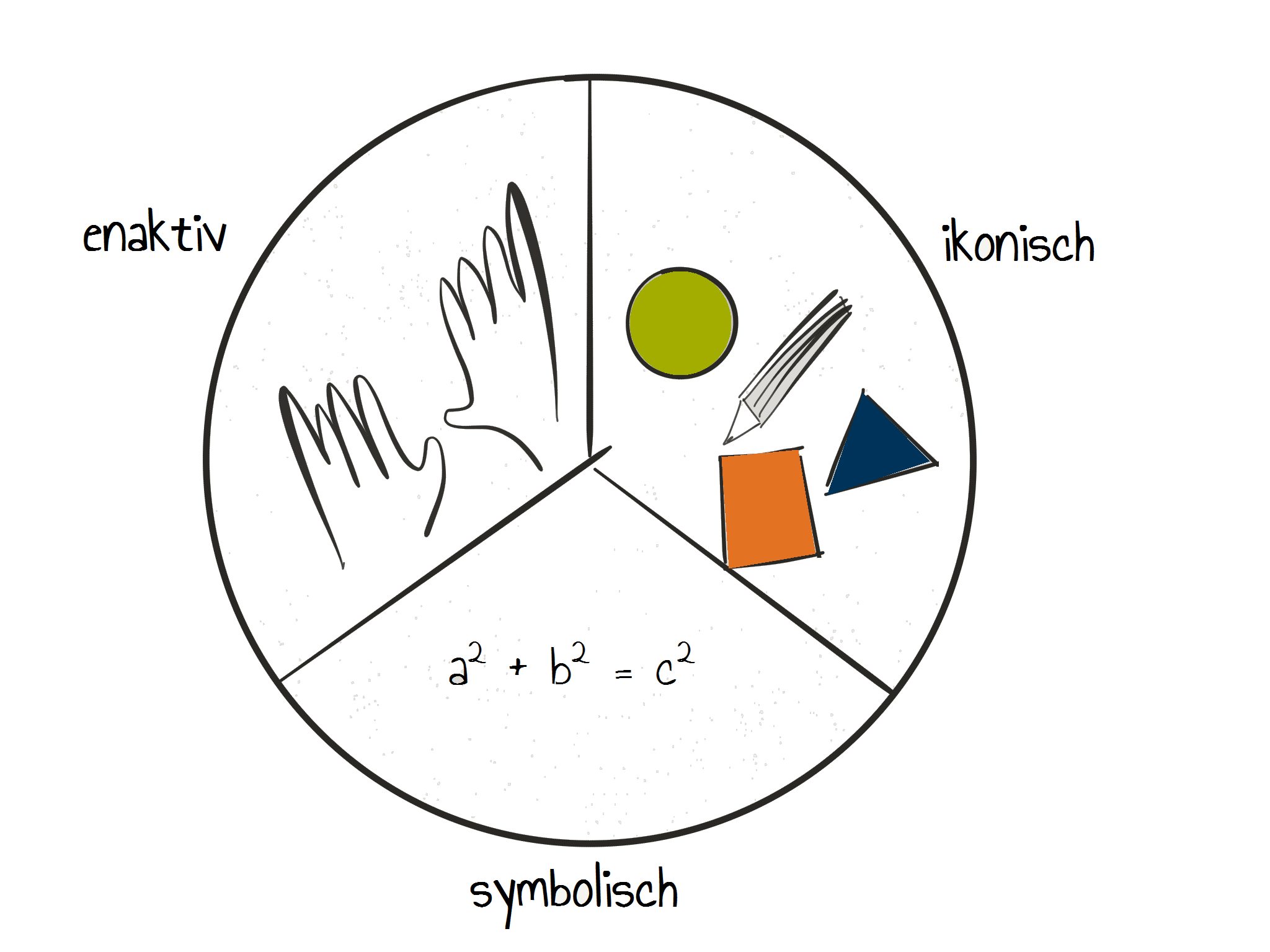
Nimmt man die Anfangsbuchstaben der drei Ebenen, ergibt sich das Wort EIS. Unterrichten nach dem EIS-Prinzip bedeutet, dass der Unterricht nach den drei Ebenen ausgerichtet wird und möglichst häufig der Ebenenwechsel geübt wird.
Die drei Ebenen bauen auch nicht zwangsläufig aufeinander auf. Das hierarchische Anordnen der Ebenen kann allerdings das Lernen erleichtern und ist nicht von den Altersstufen abhängig. Werden die Zusammenhänge und wechselseitigen Beziehungen zwischen den Ebenen herausgearbeitet, so fällt es den Lernenden leichter, zwischen ihnen zu transferieren und zu wechseln (intermodaler Transfer). Ziel ist es, dass die Lernenden auf allen Ebenen den Stoff sicher beherrschen und mühelos die Darstellung wechseln können.
Beispiele
- Bruchzahlen werden mit Hilfe von Papierrechtecken auf der enaktiven Ebene eingeführt. Faltet man ein Rechteck einmal, entstehen zwei Hälften. Faltet man diese noch einmal, entstehen vier Viertel. Der Wert des Bruches ist aber immer 1 (das gesamte Papierrechteck). Damit lässt sich das Kürzen beziehungsweise Erweitern leicht veranschaulichen. Haben die Lernenden das Rechteck als reales Modell verstanden, reicht für das Einführen von weiteren Operationen eine Zeichnung des Rechtecks, auf der dann die Faltungen angedeutet werden. Dies entspricht der ikonischen Ebene. Werden die Bruchzahlen sicher beherrscht, reicht zum Einführen neuer Inhalte die symbolische Ebene, also die Zahlen an sich.
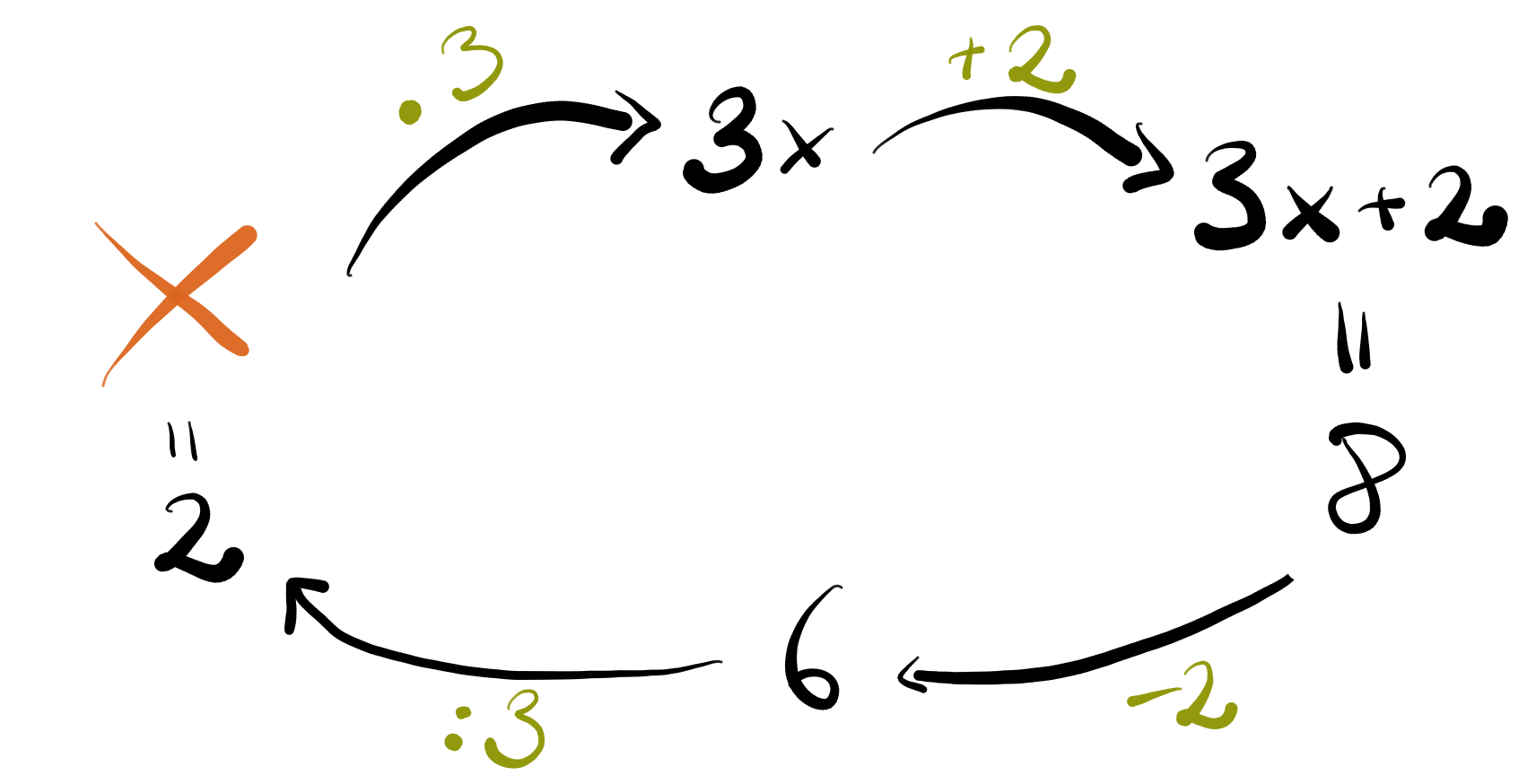
- Ein weiteres Beispiel nach Reiss & Hammer (2013) veranschaulicht die drei Ebenen an dem Beispiel der Funktion 3x + 2 = 8. Auf der enaktiven Ebene können Schachteln und Stifte die Zahlen ersetzen. Hier wird gefragt, wie viele Stifte man in die Schachteln legen muss, damit auf beiden Seiten des Gleichheitszeichen gleich viele Stifte liegen. Die Schachteln müssen dabei immer mit der gleichen Anzahl Stifte gefüllt werden. Führt man die Handlung mit Stiften tatsächlich aus, so kann die Gleichung durch Ausprobieren schon im Primarbereich gelöst werden. Auch die Äquivalenzumformung “-2” kann leicht verdeutlicht werden, wenn rechts und links einfach zwei Stifte weggenommen werden.
Auf der ikonischen Ebene kann zur Lösungsfindung der Gleichung das Spiel “Ich denke mir eine Zahl…” zur Verdeutlichung genutzt werden. Zeichnet man den Weg des Spieles auf, wird der Lösungsweg als Umkehroperation ersichtlich. In diesem Beispiel ist der Weg: Ich denke mir eine Zahl, multipliziere sie mit 3, addiere 2 und lande bei der 8. Was war meine Zahl?
Die Darstellung der Funktion als Graph liegt natürlich auch auf der ikonischen Ebene, empfiehlt sich aber nicht bei einem Anfangsunterricht. Auf der symbolischen Ebene sind die Äquivalenzumformungen der sichere Weg zur Lösung der Gleichung. Hier empfiehlt es sich, die Umformung als Umkehrung der Rechenoperation zu festigen, was im Einklang mit der Lösungsfindung auf der ikonischen Ebene steht.