Flächengleichheit bei bestimmten Verformungen
Im Folgenden werden geometrische Verformungen benutzt, die den Flächeninhalt einer Figur nicht verändern. Diese Methode wird in dem Unterrichtsvideo Szene 2: Graphische Erläuterung zum Scherungsbeweis angesprochen. Die Lehrerin lässt die Schülerinnen und Schüler mithilfe einer interaktiven Visualisierung Zusammenhänge beim Satz des Pythagoras herausfinden. So erleben sie, dass diese Operationen Stück für Stück die Flächen $a^2$ und $b^2$ in die Fläche $c^2$ verformen.
In Szene 4: Beweisführung und Hausaufgabenstellung fasst die Lehrerin die erarbeiteten Eigenschaften zusammen. Durch Scherung und Drehung von Figuren wird der Nachweis des Satzes erhalten, wobei bei diesem Verfahren der Flächeninhalt unverändert bleibt.
Die folgende dynamisch-interaktive Visualisierung, welche in Szene 2: Graphische Erläuterung zum Scherungsbeweis in ähnlicher Form Anwendung fand, veranschaulicht den Beweis nochmals:
Anleitung: Den weißen Punkt in der linken Figur hin und her bewegen. Den Schieberegler auf der rechten Seite von unten nach oben schieben.
Wenn man den Schieberegler schiebt, können drei verschiedene Phasen der Bewegung beobachtet werden. Bei der Ersten handelt es sich um eine Scherung der Quadrate $a^2$ und $b^2$ (unter Scherung ändert sich der Flächeninhalt nicht). Hierdurch werden die Quadrate zu Parallelogrammen. In der zweiten Phase werden diese Parallelogramme ein Stück nach unten verschoben (auch unter Verschiebung ändert sich der Flächeninhalt auch nicht). In der dritten Phase werden nun die beiden Parallelogramme nochmals geschert und werden zu zwei Rechtecken, die das gesamte Quadrat $c^2$ ausfüllen, wenn das Dreieck rechtwinklig ist. Ist das Dreieck nicht rechtwinklig, so sind $a^2$ und $b^2$ zusammen größer oder kleiner als $c^2$.
Beweis:
In der obigen Visualisierung ist schön zu sehen, dass $a^2$ und $b^2$ durch Verschiebung und Scherung kongruent zu $c^2$ sind. Es fehlt jedoch der Beweis, weshalb die senkrechten Seiten der Parallelogramme tatsächlich genauso lang sind wie die Hypotenuse des rechtwinkligen Dreiecks und deshalb die Verschiebung nach $c^2$ exakt passt. Erst dann ist der Satz des Pythagoras tatsächlich bewiesen.
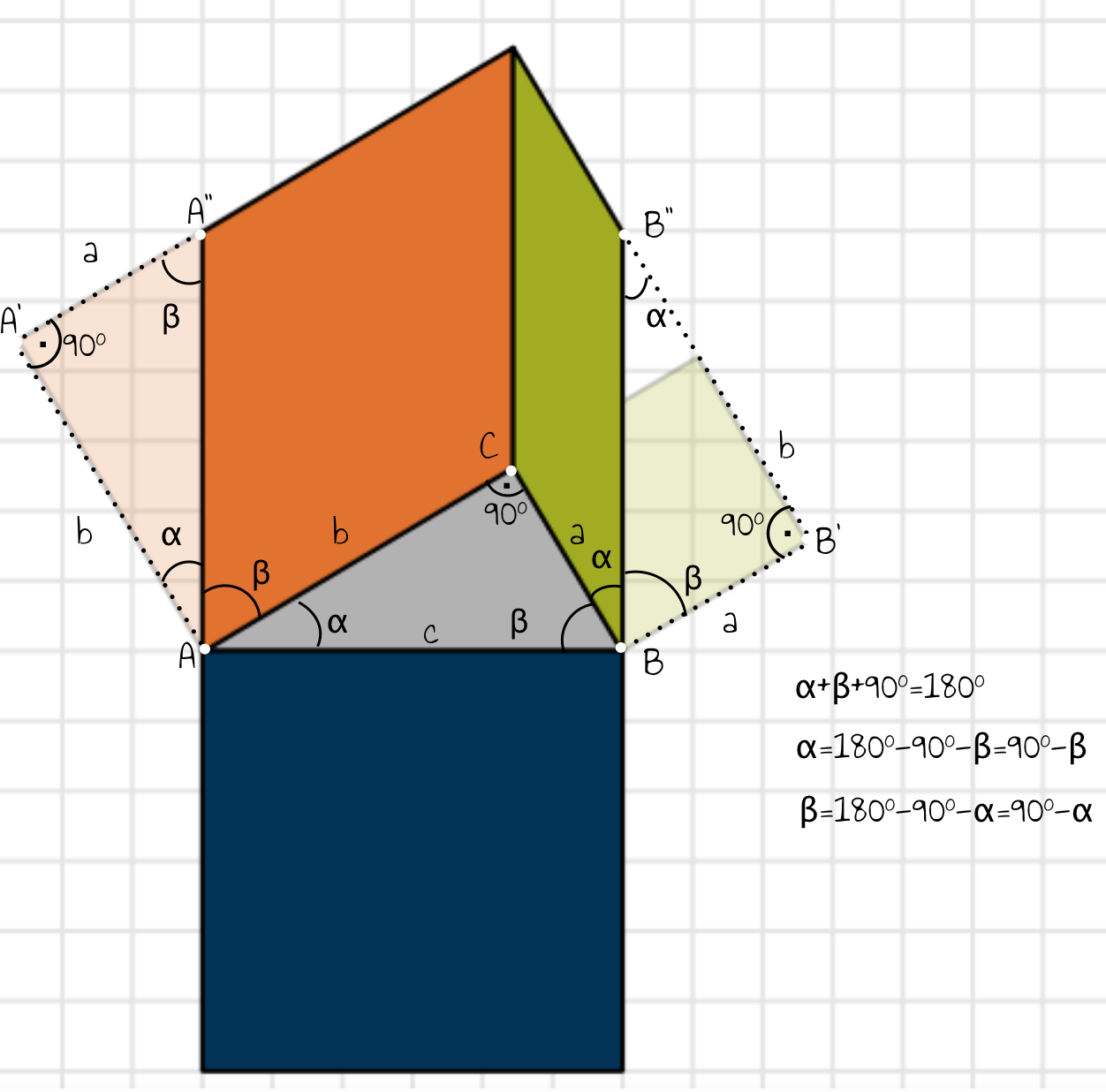
Wir zeigen, dass die Dreiecke $\triangle AA’A’’$ und $\triangle BB’B’’$ kongruent zum rechtwinkligen Dreieck $\triangle AB$ sind. So beweisen wir, dass die senkrechten Seiten der Parallelogramme genauso lang sind wie die Hypotenuse unseres rechtwinkligen Dreiecks.
Da die Innenwinkelsumme jedes Dreiecks $180°$ beträgt und das Dreieck einen rechten Winkel hat, gilt $\alpha=90°-\beta$ und $\beta=90°-\alpha$.
Nach der Scherung befinden sich die senkrechten Außenseiten der Parallelogramme im rechten Winkel zur Hypotenuse des rechtwinkligen Dreiecks ($\angle BAA”=90$ und $\angle ABB”=90$). Daher sind die Innenwinkel der Parallelogramme an den Punkten $A$ beziehungsweise $B$ gleich $\beta$ beziehungsweise $\alpha$ (da $90°-\alpha=\beta$ und $90°-\beta=\alpha$).
Außerdem ist $\angle CAA’=90$ und $\angle CBB’= 90$ (da $A’$ und $B’$ zwei Ecken der Quadrate vor der Scherung darstellen) und somit ist $\angle A’AA’’=\alpha$ und $\angle B’BB’’=\beta$ (da wiederum $90°-\alpha=\beta$ und $90°-\beta=\alpha$).
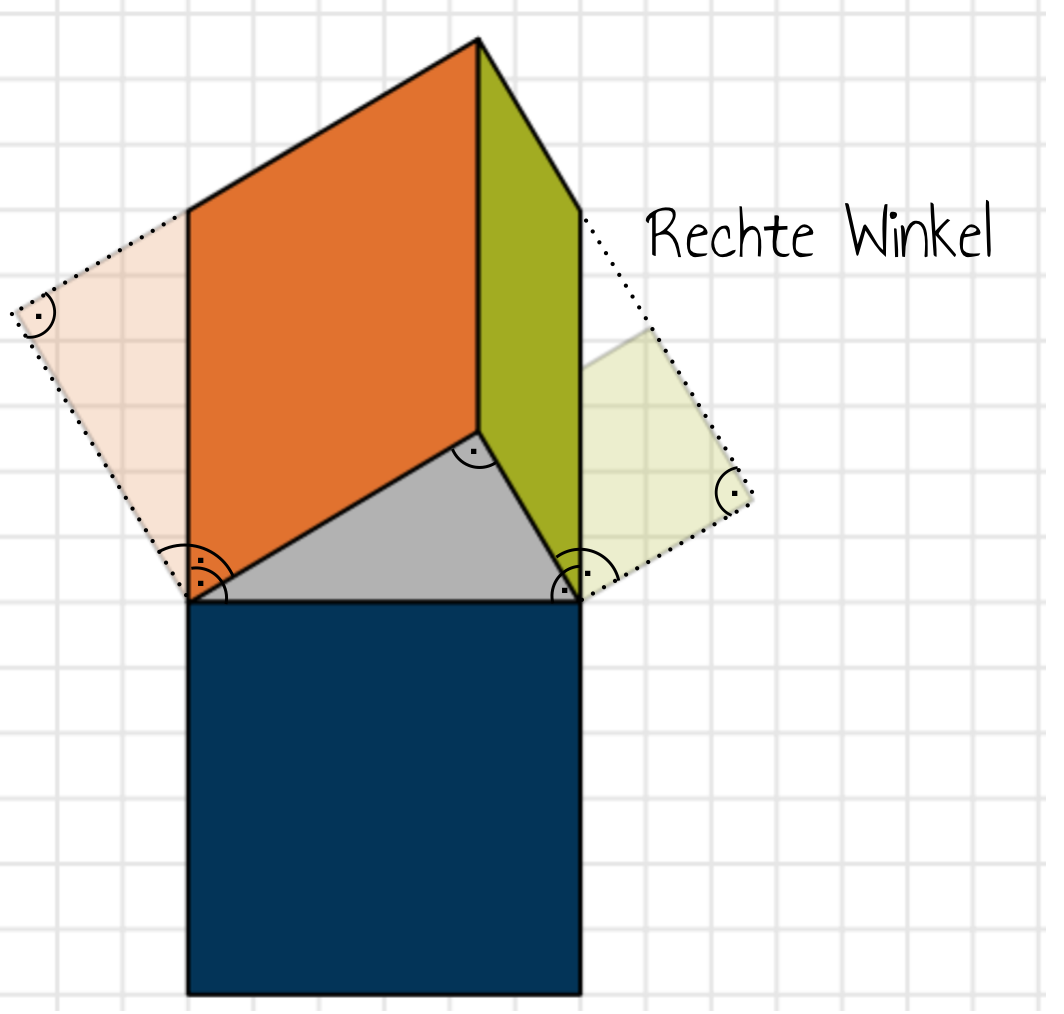
Wir kennen damit bereits einen Winkel der Dreiecke $\triangle AA’A’’$ und $\triangle BB’B’$. Da wie bereits erwähnt $A’$ und $B’$ Ecken der Quadrate bezeichnen, stehen die Seiten zu diesen Punkten senkrecht aufeinander.
Aufgrund des Innenwinkelsummensatzes für Dreiecke gilt $\triangle A’A’‘A=180°-90°-\alpha=90°-\alpha=\beta$ und $\triangle B’B’‘B=180°-90°-\beta=90°-\beta=\alpha$.
Somit sind die Innenwinkel der Dreiecke $\triangle AA’A’$ und $\triangle BB’B’$ identisch zu denen im rechtwinkligen Dreieck.
Außerdem sind die Seiten $BB’$ und $AA’$ genauso lang wie $a$ und $b$ (da $BB’$ und $AA’$ Quadratseiten sind).
Aufgrund der Kongruenzsätze für Dreiecke (WSW) sind demnach $\triangle AA’A’$ und $\triangle BB’B’$ kongruent zu $\triangle AB$. Die Hypotenusen der Dreiecke sind daher gleich lang. Nachdem die senkrechten Außenseiten der Parallelogramme jeweils eine Hypotenuse der Dreiecke $\triangle AA’A’‘$und $\triangle BB’B’$ darstellen, haben wir den Satz des Pythagoras bewiesen.