Der Beweisprozess

(Brunner, 2014; Weigand et al., 2009)

Für den Mathematikunterricht ist es sinnvoll, zwischen dem Produkt „Beweis“ und dem Prozess der „Beweisfindung“ zu unterscheiden. Während der fertige Beweis als Produkt den formalen Kriterien der Mathematik entsprechen muss, ist die Beweisfindung ein deutlich kreativerer und problemlösender Prozess, der eher unregelmäßig und sprunghaft verläuft. Da Beweisen eine Form des Problemlösens ist, kann der Beweisprozess mit dem Problemlöseprozess verglichen werden, den Sie im Modul Motivation - Problemlösen - Quadrat- und Dreieckszahlen finden. Wir wollen unseren Fokus auf den Prozess legen, die fertigen Produkte lassen sich im fachwissenschaftlichen Teil dieses Moduls nachlesen.

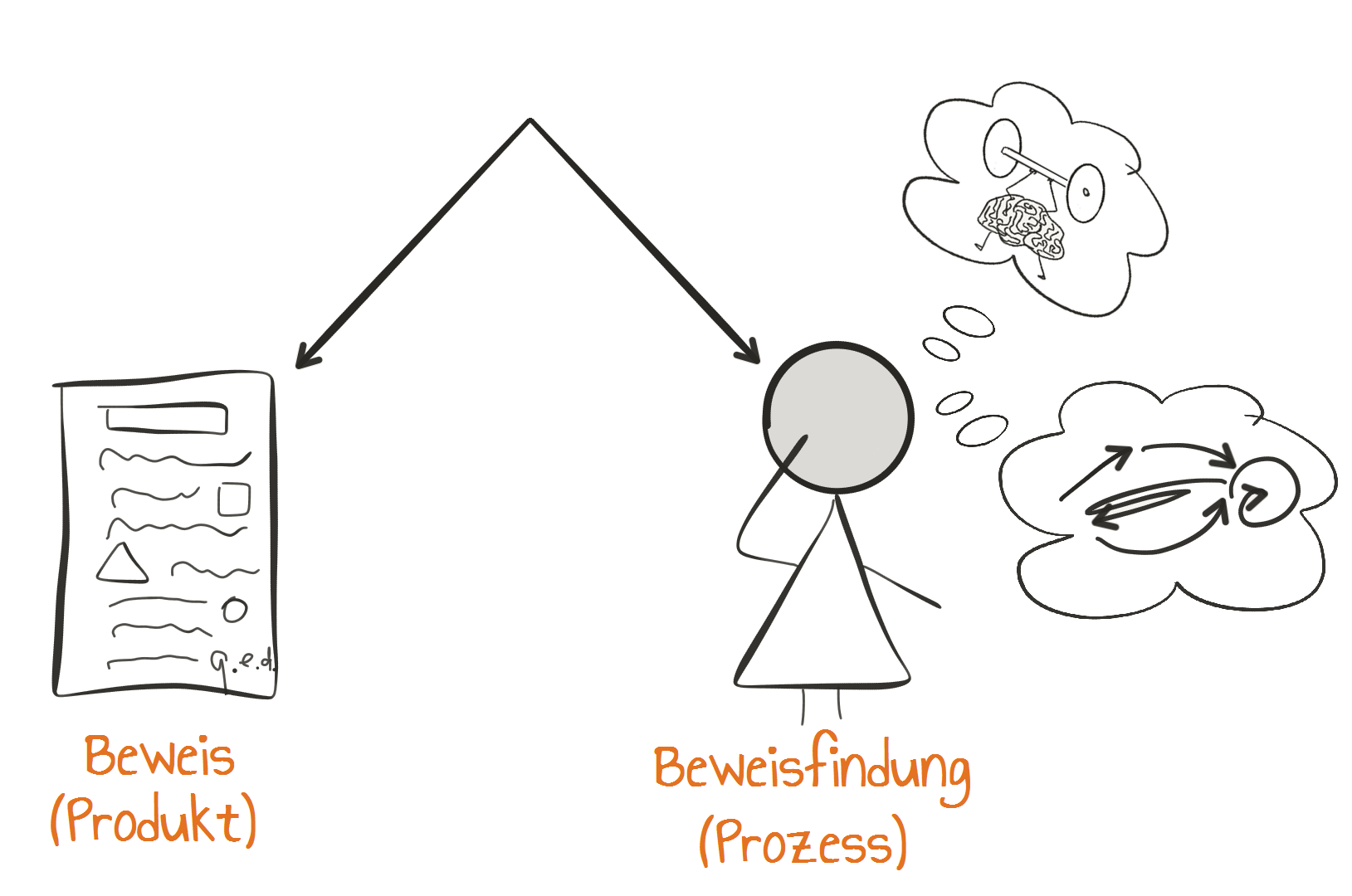
Ausgangspunkt der Beweisfindung ist ein kognitiver Konflikt. Dieser stellt eine klassische Problemaufgabe dar, denn ein unerwünschter Anfangszustand muss in den gewünschten Endzustand überführt werden, ohne dass klare Vorgehensweisen oder Strategien dafür bekannt sind. Für das formal-deduktive Beweisen werden formal-logische Schlüsse verlangt, für die anderen Beweisformen sind verschiedene Schlussformen möglich.

Der Beweisprozess sollte in den explorativen und entdeckenden Unterricht mit einer Vielzahl von Aktivitäten eingebettet werden. Nur dann können die Lernenden selbst aktiv und kreativ werden. Erste Überlegungen und Argumentationsschritte können in der Alltagssprache geschehen, später wird sukzessive die Fachterminologie integriert. Ziel dieser autonomen Übungsphase ist die formale Darstellung, die mit inhaltlichen Vorstellungen verknüpft bleiben sollte.

Aus den Zielen des Beweisens und Argumentierens im Unterricht lassen sich zwei methodische Folgerungen ziehen:

• Beweisen sollte möglichst als Dialog, also als ein offenes Argumentieren, gestaltet sein und muss nicht in einem vollständigen Beweis enden. Es sollte ein flexibler Prozess sein.
• Beweisen sollte möglichst eine inhaltliche Interpretation liefern und nicht an einer formalen Struktur orientiert sein.