Grundlagen zum Beweisen und Argumentieren
(Duval, 1991; Kultusministerkonferenz, 2012; Wittmann, 2014)
Einordnung der Begriffe Beweisen und Argumentieren
Um die Begriffe besser vergleichen zu können hat Duval (1991) das Begründen als Oberbegriff eingeführt. Das Argumentieren und Beweisen sind folglich zwei spezifische Formen des Begründens, die sich im Kontext unterscheiden. Dadurch wird es möglich, die unterschiedlichen Formen und Methoden des Beweisens, Argumentierens und Begründens besser voneinander zu trennen.
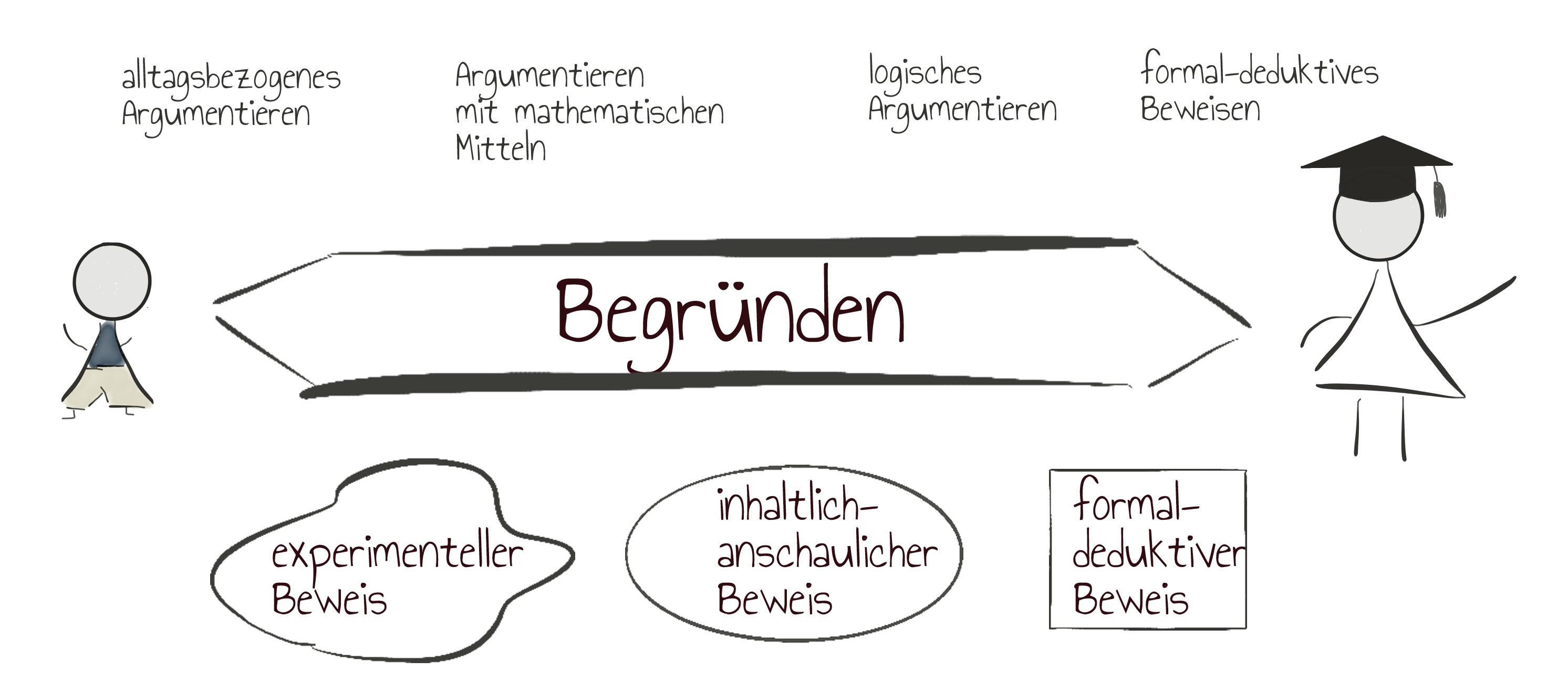
Die drei Beweistypen können als Abfolge von drei Stufen der Wissensentwicklung als Beschreibung eines genetischen Vorgehens ausgelegt werden. Ausgehend vom experimentellen Beweis, der keine Allgemeingültigkeit besitzt, wird durch den operativen Zugang eine intuitive Einsicht in die Struktur erlangt. Diese muss anschließend noch formal-symbolisch ausgedrückt werden. Dieser Verstehensprozess sollte im Unterricht durch passende Aufgaben begleitet werden.
Was muss für einen Beweis gelten?
(Wittmann, 2014)
Nach Wittmann (2014, S.36) muss ein mathematischer Beweis den folgenden Ansprüchen genügen:
-
Lückenlosigkeit und Vollständigkeit: Ein Beweis sollte mit Hilfe der logischen Schlussregeln lückenlos und vollständig darlegen, dass die Behauptung aus den Voraussetzungen sowie Axiomen und Definitionen folgt.
-
Minimalität: Ein Beweis sollte sich nur auf diejenigen Voraussetzungen stützen, die für die Gültigkeit der Behauptung nötig sind. Ferner sollten die einzelnen Argumentationsschritte keine Redundanzen enthalten.
-
Formalisierung von Struktur, Sprache und Symbolik: Beweise werden häufig in einer formalisierten Struktur präsentiert. Gleiches gilt für die gepflegte Fachsprache, die ein hohes Maß an Präzision mit sich bringt.
Welche Beweistechniken werden in der Schule verwendet?
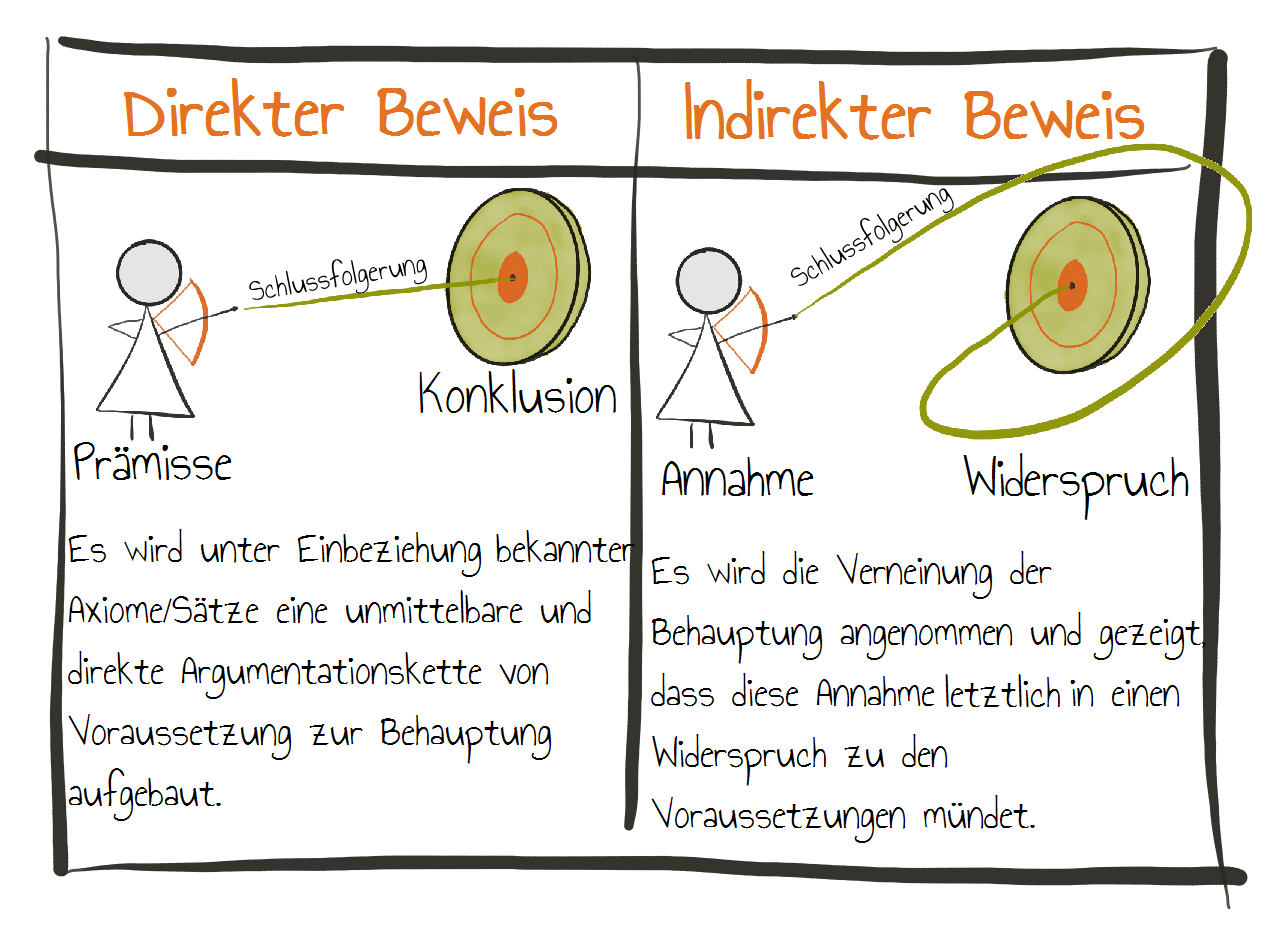
Die unterschiedlichen Beweise, die im fachwissenschaftlichen Teil vorgestellt werden (Beweise zum Satz des Pythagoras) sind allesamt direkte Beweise. Überlegen Sie sich warum!
Bezug zu den Bildungsstandards
(Kultusministerkonferenz, 2012)
Die Kompetenz K1 Mathematisches argumentieren beinhaltet:
- Fragen stellen, die für die Mathematik charakteristisch sind („Gibt es…?“, „Wie verändert sich…?“) und Vermutungen begründet äußern
- mathematische Argumentationen entwickeln
- Lösungswege beschreiben und begründen
Elemente, wie „Beurteilen Sie…“, „Geben Sie eine Begründung an für…“, wirken in einer Aufgabe kompetenzfördernd. Die drei Anforderungsbereiche sind jeweils erreicht, wenn die Lernenden folgendes beherrschen:
- Anforderungsniveau 1: Routineargumentationen (bekannte Sätze, Verfahren, Herleitungen) wiedergeben und anwenden; einfache rechnerische Begründungen angeben; mit Alltagswissen argumentieren
- Anforderungsniveau 2: Überschaubare mehrschrittige Argumentationen nachvollziehen, erläutern oder entwickeln
- Anforderungsniveau 3: Komplexe Argumentationen nutzen, erläutern oder entwickeln; verschiedene Argumente nach Kriterien wie Reichweite oder Schlüssigkeit bewerten