Aufgaben im Unterricht

(Böhm, 2013; Greefrath, 2010 & 2018; Greefrath et al., 2013; Jahnke, 2005; Landerl, 2016; Maaß, 2010, 2014; Neubrand et al., 2011; Reiss & Hammer, 2013; Wess, 2020)

Modellierungsaufgaben

Modellierungsaufgaben, wie etwa Fermi-Aufgaben, und eingekleidete Aufgaben, beispielsweise simple Textaufgaben, sind grundsätzlich voneinander zu unterscheiden (Reiss & Hammer, 2013). So sind eingekleidete Aufgaben ohne tatsächlichen Realitätsbezug verfasst und haben zum Ziel, mathematische Fachausdrücke einzuüben oder Zusammenhänge anzuführen. Sie haben einen rechnerischen Schwerpunkt (Wess, 2020, S. 24). Um Modellierungsprozesse zu initiieren, eignen sie sich daher nur eingeschränkt. .

Modellierungsaufgaben zeichnen sich durch ihre Authentizität und Realitätsnähe aus. Sie können durch ihr kognitives Aktivierungspotential klassifiziert werden oder hinsichtlich der Aktivität der Lernenden im Sinne von Aufgaben für das Lernen (Erforschen, Systematisieren, Üben) und Aufgaben für das Leisten (Kompetenz, Überprüfung, Bewertung) (Wess, 2020, S. 25). Auch die Ausprägung der Offenheit hinsichtlich der Herangehensweisen der Lernenden ist eine Möglichkeit der Klassifizierung. Ein hoher Offenheitsgrad im Sinne des Potentials, mehrere Lösungswege einzuschlagen, kann im Hinblick auf den Anfangszustand, die Transformation und den Zielzustand kategorisiert werden.

Nach Wess (2020) lassen sich, angelehnt an Greefrath et al. (2017, S. 936), folgende Kriterien für die Entwicklung von Modellierungsaufgaben festhalten:

• Realitätsbezug: Die Problemstellung hat einen außermathematischen Bezug.
• Relevanz: Die Problemstellung wird seitens der Lernenden als interessant eingestuft, im Sinne eines Bezuges zu ihrer Lebenswelt.
• Authentizität: Hinsichtlich des außermathematischen Sachbezugs erweist sich die Aufgabenstellung als authentisch.
• Offenheit: Die Problemstellung der Modellierungsaufgabe ist hinsichtlich des Lösungswegs offen konzipiert und lässt damit unterschiedliche Lösungsansätze zu. Dies gilt bestenfalls auch für das Niveau.
• Förderung von Teilkompetenzen: Kognitive Teilkompetenzen des mathematischen Modellierens werden von der Problemstellung begünstigt.

Realitätsgehalt der Aufgaben

Die mathematische Modellierung findet immerzu in außermathematischen Problemstellungen ihren Ursprung. Der Grad der realistischen Beschaffenheit der zu betrachtenden Gegebenheit kann unterschiedliche Qualitäten aufweisen. So ist etwa die Erdumfangsberechnung für die Menschen der Antike weitaus relevanter als für heutige Lernende. Aus diesem Grund gestaltet sich der Realitätsgehalt, ferner der Anspruch daran, zum einen infolge der zugrundliegenden realen Situation und zum anderen infolge des Realitätsgehalts der Aufgabenstellung im Sinne der Problemdarstellung. Dabei sind etwa Aufgaben, die das Thema Glücksspiel behandeln, oftmals unpräzise in ihrem Realitätsbezug (vgl. Böhm, 2013).

Es ist festzuhalten, dass zumeist gewinnbringende didaktische Mechanismen zugunsten der Qualität der Realitätsdarstellung ausfallen. In diesem Zusammenhang ist die Definition für authentische Situationen nach Maaß (2004, S. 22) grundlegend, zumal im PISA-Framework festgehalten worden ist, dass authentische Aufgabenstellungen in internationalen Tests präferiert werden:

„Eine authentische Situation ist eine außermathematische Situation, die in ein bestimmtes Gebiet eingebettet ist und sich mit Phänomenen und Fragen beschäftigt, die für dieses Gebiet bedeutsam sind und von den entsprechenden Fachleuten auch als solche erkannt werden. Dabei gilt auch der Alltag als ‘Gebiet’ und hier die Menschen, die in ihm leben als ‘Fachleute’. Eine Situation wird auch als authentisch angesehen, wenn sie im Unterricht simuliert wird.“

Neben authentischen Situationen finden wir realitätsbezogene Situationen, die hiervon abweichende Eigenschaften besitzen. Angelehnt an Neubrand et al. (2011, S. 56), sind realitätsbezogene Situationen solche, deren Informationen zwar reale Bedeutung haben, aber für den didaktischen Gebrauch konstruiert worden sind. Die Präferenz liegt also bei der Aufgabenstellung im schulpraktischen Kontext. Der Grad der Realitätsbezogenheit erstreckt sich hier von einer Realitätsnähe bis hin zu eingekleideten Aufgabenstellungen.

Hinsichtlich des Aspekts der Authentizität von Aufgaben, sei angemerkt, dass unter anderem Jahnke (2005) an der Wirklichkeit authentischer Aufgaben zweifelt, da diese immer für den schulpraktischen Kontext erstellt werden. Sie haben die Eigenschaft, Lernprozesse anzustoßen, die auf Lehrplanvorgaben beruhen.

Videobeispiel

In Szene 1: Hausaufgabenbearbeitung der Modellierungsaufgabe sehen wir eine Schülerin eine Aufgabe zum Wachstum von Milchsäurebakterien bearbeiten. Bei dieser Aufgabe handelt es sich um eine eingekleidete Aufgabe. Sie hat zwar einen Realitätsbezug, ist aber eindeutig für didaktische Zwecke erstellt worden. Umweltfaktoren, wie die Temperatur der Milch oder der Luftdruck, die das Bakterienwachstum beeinflussen könnten, werden nicht mit in die Berechnung integriert. Sie würden die Komplexität der Aufgabe sonst zu sehr erhöhen.

Überlegen Sie sich, wie jeweils eine eingekleidete Aufgabenstellung und eine realitätsbezogene Situation im Mathematikunterricht aussehen könnte.

Fermi-Aufgaben

Wie viele Klavierstimmer gibt es in Chicago? Das ist wohl die berühmteste Fermi-Aufgabe, die der Physiker und Nobelpreisträger Enrico Fermi (1901-1952) seinen Studierenden gestellt hat. Was zunächst auffällt, ist, dass keine Informationen vorzufinden sind (Greefrath, 2018; Landerl, 2016). Um eine solche Aufgabe zu lösen, bedarf es einer schrittweisen Herangehensweise, etwa über die Ermittlung der Einwohner Chicagos, der Haushaltsgrößen, den Haushalten mit Klavieren und dem zeitlichen Abstand zwischen den Klavierstimmungen oder auch der Dauer des Klavierstimmens.

Hieran wird deutlich, dass sich Fermi-Aufgaben, die zu den Modellierungsaufgaben gezählt werden, durch ihren Offenheitsgrad auszeichnen, was sie für die Lernenden ungemein zugänglich macht. Durch eine gestufte Schätzung können Zwischenergebnisse festgehalten und ein Ergebnis hervorgebracht werden. Weiterhin werden unter Fermi-Aufgaben grundsätzlich mathematische Aufgabenstellungen, die lediglich aus einem Satz bestehen, verstanden; einen einzig richtigen Lösungsweg gibt es nicht (Greefrath, 2010; Reiss & Hammer, 2013).

Im schulpraktischen Kontext steht bei diesem Aufgabentypus das Rechnen eher im Hintergrund und etwa das Vereinfachen oder das Validieren im Vordergrund (Greefrath, 2018). Lernende werden hier veranlasst, heuristisch-strategische Vorgehensweisen mithilfe ihres Alltagswissens zu erproben.

Landerl (2016), gibt eine Zusammenschau der Charakteristika von Fermi-Aufgaben (angelehnt an Leufer et al., 2010, S. 7):

• Realitätsbezug: Fermi-Aufgaben zeichnen sich durch einen starken Bezug zum Alltag aus und werden durch eine Frage gestellt: Wie viele Haare hat ein Mensch durchschnittlich auf dem Kopf?
• Zugänglichkeit: Der beträchtliche Realitätsbezug verspricht eine ebenso deutliche Zugänglichkeit für Lernende.
• Herausforderung: Es existieren zahlreiche Fermi-Aufgaben und sie stellen die Lernenden stets vor neue Herausforderungen. Sie versprechen eine klare Abwechslung vom sonstigen Mathematikunterricht.
• Offenheit: Fermi-Aufgaben zeichnen sich durch ihren hohen Offenheitsgrad im Sinne vieler möglicher Lösungsmöglichkeiten aus. Dabei ist es von Bedeutung, die unterschiedlichen Lösungswege und Ergebnisse der Lernenden miteinander zu vergleichen, um so einen wahrscheinlichen Lösungsweg festzuhalten und unwahrscheinliche Lösungsansätze auszumachen.
• Kompetenzen: Fermi-Aufgaben ermöglichen es, unterschiedlichste Kompetenzen zu erwerben oder zu festigen; dies betrifft insbesondere die Modellierungsschritte des Vereinfachens und des Validierens (Greefrath, 2010, S. 81).
• Anregung: Dieser Aufgabentypus initiiert die tiefere und selbstständige Auseinandersetzung verschiedener Themengebiete im Mathematikunterricht.
• Blick für Mathematik: Fermi-Aufgaben ermöglichen einen Perspektivenwechsel und lassen die Alltäglichkeit und Welt-Nähe der Mathematik verstehen. Dies kann dazu führen, ein allgemeines Interesse für Mathematik herbeizuführen oder es zu verstärken.

Wie bereits erwähnt, bringen Fermi-Aufgaben viele Vorteile mit sich, so sind sie z. B. wegen ihrer Offenheit für mehrere Lösungswege kognitiv aktivierend oder fördern auch den Einsatz von heuristisch-strategischen Vorgehensweisen. Welche weiteren Potentiale, aber auch Gefahren oder Hürden, sehen Sie noch im Einsatz von Fermi-Aufgaben für Ihren Unterricht?

Historische Aufgaben

In Mathematik-Schulbüchern sind immer wieder sogenannte historische Aufgaben zu finden. Das hat vielerlei Gründe; ein prominenter Aspekt ist, Lernenden bewusst zu machen, wofür Mathematik genutzt werden kann und wie sich mathematisches Modellieren im Laufe der Geschichte entwickelt hat. Böhm (2013) hat in diesem Zusammenhang die antike Erdumfangsberechnung nach der historischen Person Eratosthenes (überliefert von Cleomedes) aufgegriffen und diese den Charakteristika von Modellen, ferner den Modellierungsprozessen zugeteilt:

• … Modellauffassung: Die durch die Übertragung der Erde als Kugel in der Realität idealisierte Erdumfangsberechnung wird auf eine elementargeometrische Berechnung mittels eines Kreises projiziert. Von der textaufgabenartigen real beschriebenen Situation über den Schatten des Obelisken in Alexandria und den Brunnen in Syene bleibt eine nur eine assoziative Abstraktion über. Der schulmathematische Zweck ergibt sich aus der Verwendbarkeit der Mathematik im historischen Kontext.
• … Bearbeitungsprozess: Die antike Darstellung des Bearbeitungsprozesses der Erdumfangsberechnung findet sich in den charakteristischen Teilprozessen des Modellierens wieder. Durch die Modifikation der Erde zu einer Kugel und die Datenbeschaffung wird eine mathematische Repräsentation generiert. So kann eine mathematische Behandlung des Gegenstands durchgeführt werden. Es wird ein mathematisches Ergebnis erbracht und anschließend in die Realität übersetzt.
• … Realitäts- und Anwendungsbezug: Es bestand (historisches) Interesse daran, den Erdumfang zu berechnen, um sich ein Bild über die Größe der Erde machen zu können. Im Schulunterricht ist es heute möglich, auf diese Weise geometrische Arbeiten einzuführen oder für diese Motivation herbeizuführen und natürlich mathematische Modellierungsprozesse zu erlernen.

Die konkrete Aufgabe kann folgendermaßen gestaltet sein und zu Beginn steht die Frage: Wie groß ist der Erdumfang? Dabei ist der realitätsbezogene Kontext die Information der historischen Umstände, in der die Frage entstanden ist: Eratosthenes stellt am Tag der Sonnenwende in Syene fest, dass er in einem tiefen Brunnen zur Mittagszeit das Spiegelbild der Sonne sieht, sonst ist das Wasser im Brunnen immer im Schatten. Gleichzeitig wirft in Alexandria ein hoher Obelisk einen Schatten. In Alexandria fielen die Sonnenstrahlen also nicht senkrecht auf die Erde, sondern mit einer Abweichung zur Senkrechten (Winkel (\alpha)).

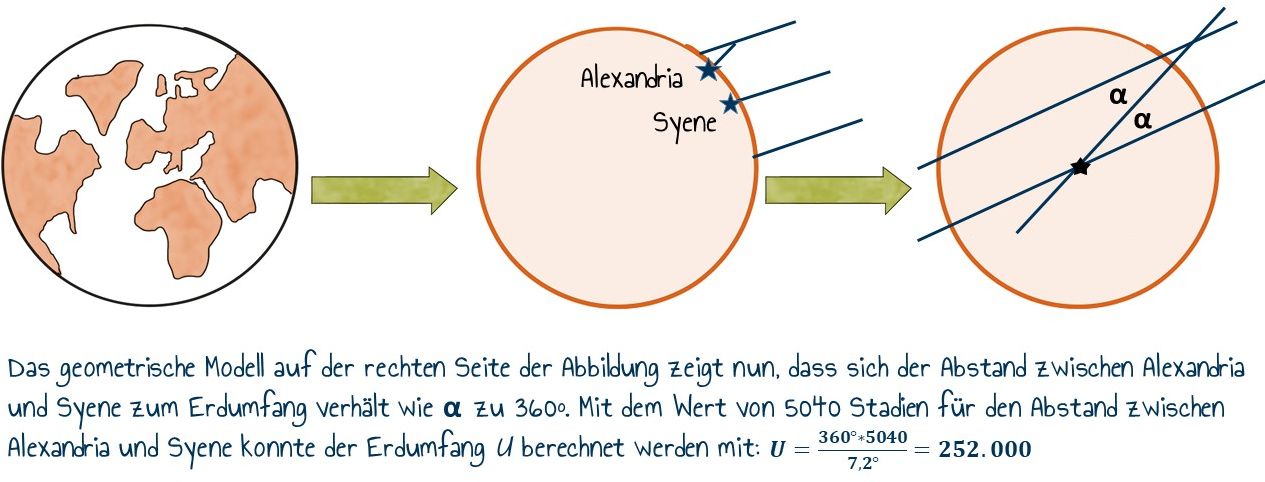Abbildung: In Anlehnung an Böhm (2013, S.19)

Aufgabe dazu…

Aufgabe 9