Kognitive Aktivierung beim Modellieren
(Ableitinger, 2010; Böhm, 2013; Borromeo Ferro, 2011; Lesh & Doerr, 2003; Jordan et al., 2008; Leuders & Holzäpfel, 2011;Niss, 2010; Schukajlow & Krug, 2012)
Grundlagen der kognitiven Aktivierung beim mathematischen Modellieren
Niss (2010) beschreibt den kognitiven Prozess beim mathematischen Modellieren und insbesondere den Prozess zur Erarbeitung eines mathematischen Modells, um auf Grundlage solcher Modellvorstellungen Konsequenzen für den Erwerb und die Vermittlung von Modellierungskompetenzen ziehen zu können. Zwar gibt es inzwischen verschiedene Studien und Beiträge, die das mathematische Modellieren aus kognitiver Perspektive betrachten, jedoch liegt bislang keine umfassende Modellvorstellung über den kognitiven Prozess vor. Grundsätzlich werden zwar wichtige Aspekte benannt und relevante Phänomene dargestellt; eine Integration der Erkenntnisse steht jedoch aus. Einen Überblick über Studien, die sich mit der kognitiven Perspektive beschäftigen, ist bei Borromeo Ferri (2011, S. 23-40) zu finden. Neben der oben angeführten Arbeit von Niss (2010), sind sind die Studien über kognitive Prozesse von Borromeo Ferri (2011) und der Beitrag von Lesh & Doerr (2003) zentral:
- Borromeo Ferri (2011): Modellierungsverläufe (individuell und in Gruppen) bei der Bearbeitung von Modellierungsaufgaben: Es wird die vorherrschende Modellvorstellung (die eine geringere Anzahl an Schritten postuliert) über den Prozess des mathematischen Modellierens infrage gestellt.
- Lesh & Doerr (2003): Der Prozess der Modellbildung ist zyklisch und iterativ, mithilfe verschiedener Repräsentationsformen werden unterschiedliche Interpretationen außermathematischer Situationen entwickelt und getestet, bis ein stabiles System gefunden ist.
Kognitive Aktivierung beim Modellieren im Mathematikunterricht
Trotz allem kann davon ausgegangen werden, dass es das Wesen des Modellierens ist, grundsätzlich kognitive Aktivierungsmöglichkeiten bei Lernenden im Modellierungsprozess und im Modelldenken anzubieten. Auch wenn das durch Aufgabenstellungen vermittelte Aktivierungspotential im Mathematikunterricht der Bundesländer zu kurz gerät (Jordan et al. 2008), kann und muss naturgemäß von einer kognitiven Aktivierung der Lernenden gesprochen werden. Es gelten folgende Merkmale des Unterrichts als konstitutiv für eine kognitive Aktivierung: “Wenn die Lehrperson mit Aufgaben das Denken der Lernenden auf einem hohen kognitiven Niveau anregt, wenn sie an deren Vorwissen anknüpft und dieses aktiviert, wenn sie Lernende eigene Ideen, Konzepte, Lösungen, etc. erklären lässt und damit flexibel und ‘evolutionär’ umgeht” (Leuders & Holzäpfel, 2011, S.213).
Das innermathematische Potenzial hinsichtlich der kognitiven Aktivierung von Lernenden ist zum einen durch die “Stimulation günstiger Eigenaktivitäten” und zum anderen durch die “Stimulation von Reflexionen” (Ableitinger 2010, S. 95) gegeben. Werden mehrere Lösungen entwickelt, ergibt sich eine hohe kognitive Aktivierung (vgl. Schukajlow & Krug, 2012). Ferner wird hier von der Beherrschung sogenannter Prozesskompetenzen, die sich durch das Problemlösen beim Modellieren entwickeln, gesprochen. Ein in diesen Zusammenhang wichtiger Aktivierungsansatz ist das Bereitstellen eines Problemlöseplans, welcher zu einer deutlichen Steigerung selbst wahrgenommener Strategien seitens der Lernenden führt.
Wie könnte ein konkreter Problemlöseplan aussehen? Wie würden Sie diesen im Allgemeinen strukturieren (Hilfekärtchen, Zusammenfassung, Video, Tipps, Einsatz von Lernstrategien,…)?
Welchen Einfluss hat der Einsatz der Simulation in Szene 4: Einstiegsphase mit Lernvideo auf die kognititve Aktivierung?
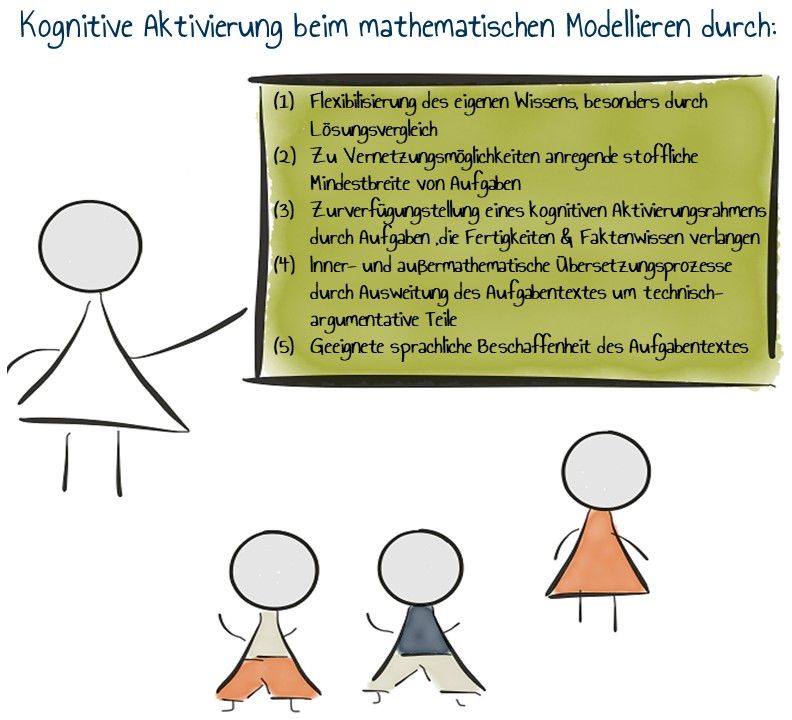
In Anbetracht dessen, dass der Löwenanteil des Mathematikunterrichts hierzulande aus der Beschäftigung mit Aufgabenstellungen besteht (Jordan et al., 2008) und somit deren kognitiv aktivierender Gehalt von hohem Wert ist, kann zusammenfassend dargestellt werden, dass eine kognitive Aktivierung beim mathematischen Modellieren unter folgenden Gesichtspunkten nach Jordan et al. (2008, S. 102) stattfindet: