Falsches Addieren
(Ford, 1938; Karpenkov, 2013; Koecher & Krieg, 2007)
Einer der häufigsten Fehler beim Addieren von Brüchen ist, dass Zähler mit Zähler und Nenner mit Nenner zusammengezählt werden. Allerdings findet diese Operation in der Mathematik einige Anwendungen und deswegen ist es wichtig, sie nicht als per se falsch abzustempeln, sondern nur als für den Kontext unpassend. Um dies zu illustrieren, seien hier drei Beispiele angeführt. Um die “falsche” Art zu Addieren von der “richtigen” zu unterscheiden, wird hier die folgende Notation verwendet:
\[\frac{a}{b}\oplus\frac{c}{d}\enspace :=\enspace \frac{a + c}{b + d}\]
Diese Operation wird manchmal Farey-Summe genannt und hat u.a. Verbindungen zu Kettenbrüchen (Karpenkov, 2013). Allerdings wird hier nur die Operation an sich kurz analysiert.
Das einfachste Beispiel in diesem Zusammenhang ist die Berechnung von Durchschnittsgeschwindigkeiten. Legt ein Läufer eine Strecke $s_1$ in der Zeit $t_1$ zurück und anschließend die Strecke $s_2$ in der Zeit $t_2$, und nimmt man an, er hat beide Teile mit jeweils konstanter Geschwindigkeit zurückgelegt, so ist seine Durchschnittsgeschwindigkeit insgesamt gleich
\[\frac{s_1 + s_2}{t_1 + t_2}\enspace =\enspace \frac{s_1}{t_1}\oplus\frac{s_2}{t_2}.\]
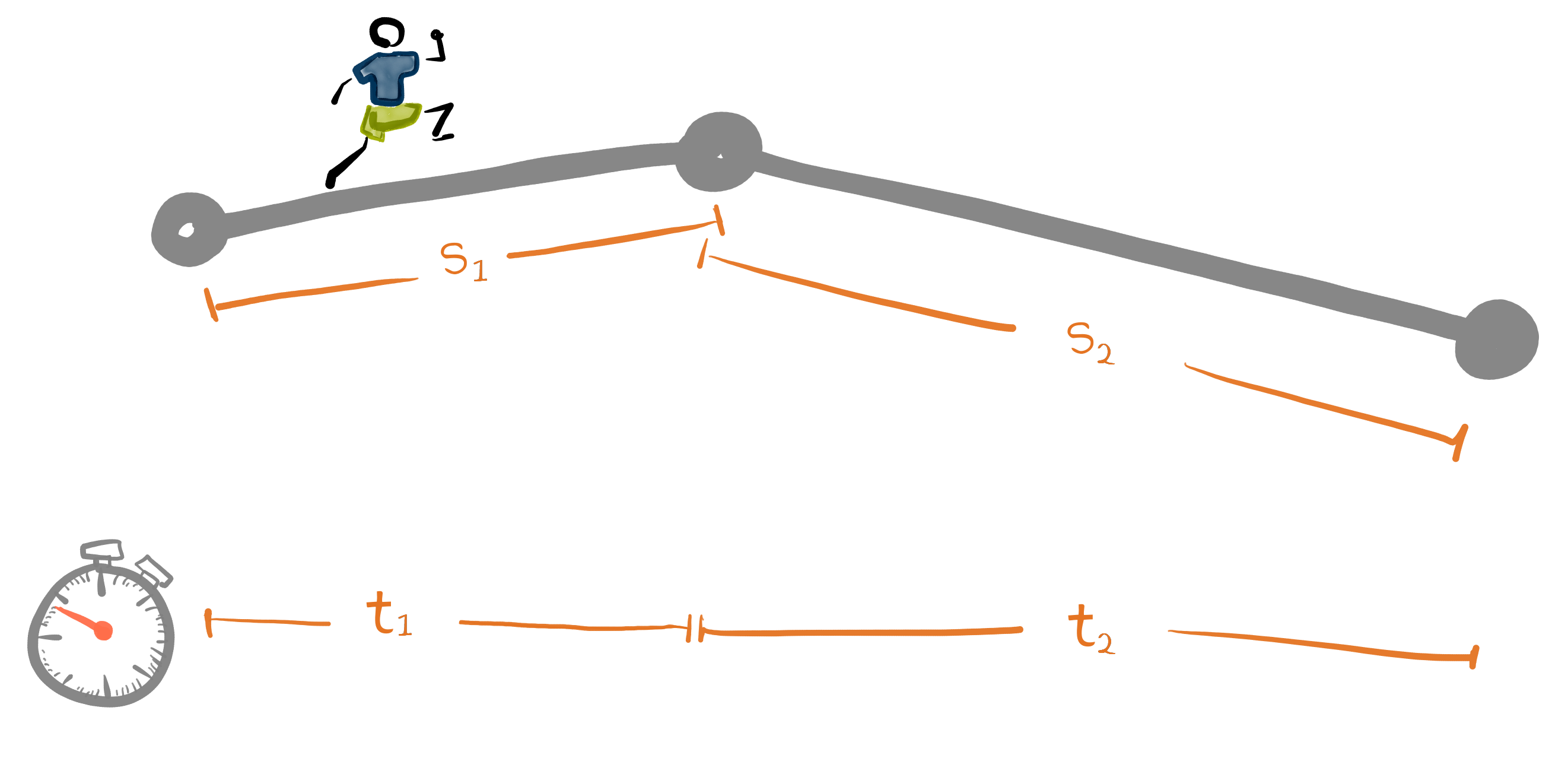
Mit diesem Beispiel kann man sehr schön erklären, dass diese Art zu Addieren auch Brüche “zusammenfasst”, dies aber auf essenziell andere Art und Weise geschieht als die gewöhnliche Bruchaddition. Wenn Brüche Geschwindigkeiten (oder Ähnliches) modellieren, so ergibt diese Operation Sinn. Allerdings heißt das automatisch, dass das Ergebnis $\frac{s_1}{t_1}\oplus\frac{s_2}{t_2}$ immer zwischen den Ausgangswerten $\frac{s_1}{t_1}$ und $\frac{s_2}{t_2}$ liegen muss. Da Brüche als “normale” Zahlen aber Längen darstellen, muss das Ergebnis immer größer als die Ausgangswerte sein, zumindest, solange es um positive Zahlen geht. Anstatt also Lernenden sagen zu müssen, dass (rein arithmetisch) das falsche Ergebnis herauskommt, wenn Brüche auf diese Art addiert werden, kann es über dieses Beispiel klar veranschaulicht werden.
Ein weiteres, eng verwandtes Beispiel, das die Problematik noch stärker betont, ist die Berechnung von Mischverhältnissen, in der Chemie ganz allgemein oder konkret z. B. beim Kochen oder in der Fotografie. Sind etwa zwei Gefäße mit einer Salzlösung gegeben und beträgt die Konzentration im ersten Gefäß $\frac{3}{10}$ und im zweiten $\frac{9}{10}$, stellt sich die Frage, welche Konzentration entsteht, wenn die Inhalte beider Gefäße zusammengeschüttet werden. Das hängt aber natürlich noch davon ab, welche Volumina die beiden Gefäße beinhalten.
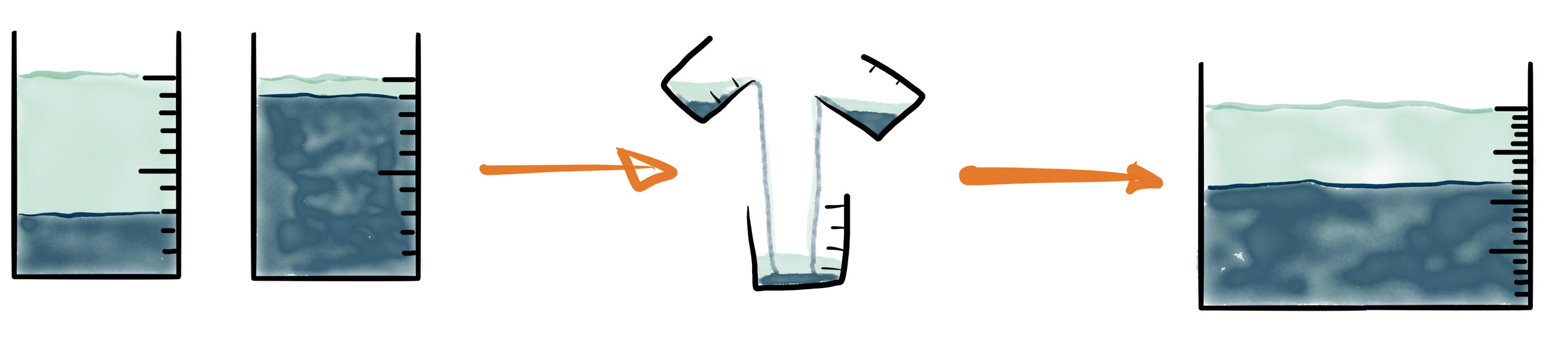
Sind sie gleich groß, kann einfach die Durchschnittskonzentration bestimmt werden: Sei $V$ das Volumen. Dann beträgt die absolute Salzmenge (die dunkelblaue Fläche in der schematischen Zeichnung oben) in Gefäß Eins gleich $\frac{3}{10}V$ und in Gefäß Zwei gleich $\frac{9}{10}V$. Somit beträgt die Salzmenge nach dem Zusammenführen $\frac{3}{10}V + \frac{9}{10}V = \frac{12}{10}V$. Das neue Gesamtvolumen ist $2V$. Somit ergibt sich ein neuer Salzgehalt von
\[\frac{\frac{12}{10}V}{2V}\enspace =\enspace \frac{12}{20}\enspace =\enspace \frac{3}{10}\oplus\frac{9}{10}.\]
Da sich $V$ herausgekürzt hat, ist es am Endergebnis nicht mehr ersichtlich, dass zwischendurch die absolute Menge an Salz in beiden Lösungen berechnet wurde. Sind beide Ausgangsvolumina unterschiedlich, so muss dieser Schritt bewusst gemacht werden, um das richtige Ergebnis zu erhalten. Hier soll nun aber der Fokus auf einer anderen Problematik liegen. Selbst wenn beide Volumina gleich sind, kann das Ergebnis uneindeutig sein. Sind die Salzgehalte etwa $\frac{2}{3}$ und $\frac{3}{4}$, so könnte die obige Rechnung vermuten lassen, dass hier der Salzgehalt nach dem Zusammenschütten $\frac{2}{3}\oplus\frac{3}{4} = \frac{5}{8}$ beträgt. Wir haben allerdings auch die Interpretation verwendet, dass der neue Salzgehalt der Durchschnitt der beiden Ausgangswerte ist. Das ergibt also $\frac{1}{2}\cdot\left(\frac{2}{3} + \frac{3}{4}\right) = \frac{17}{24}$, und dieser Wert ist klar ungleich $\frac{5}{8}$. Außerdem liefert die abgekürzte Rechnung unterschiedliche Ergebnisse, wenn einer der Brüche durch einen wertgleichen ersetzt wird: $\frac{4}{6} \oplus \frac{3}{4} = \frac{7}{10}$. Das führt zu der Frage, welches Ergebnis denn nun richtig ist. Wie eben schon im Fall unterschiedlicher Volumina angedeutet, führt im Zweifelsfall nur die Berechnung des absoluten Salzgehalts zum Ziel. Dieser ist hier $\frac{2}{3}V$ bzw. $\frac{3}{4}V$ und der neue, relative Salzgehalt beträgt somit
\[\frac{\frac{2}{3}V + \frac{3}{4}V}{2V}\enspace =\enspace \frac{17}{24}.\]
Die Interpretation, den Durchschnittswert zu berechnen, bleibt also bestehen. Beide $\oplus$-Rechnungen sind hingegen falsch. Allerdings ist der korrekte Wert das Ergebnis der Rechnung $\frac{8}{12}\oplus \frac{9}{12}$. Werden die Brüche nur passend erweitert, führt die $\oplus$-Rechnung doch zum Ziel. Der Grund dafür wird ersichtlich, wenn man sich die Situation grafisch vor Augen führt.
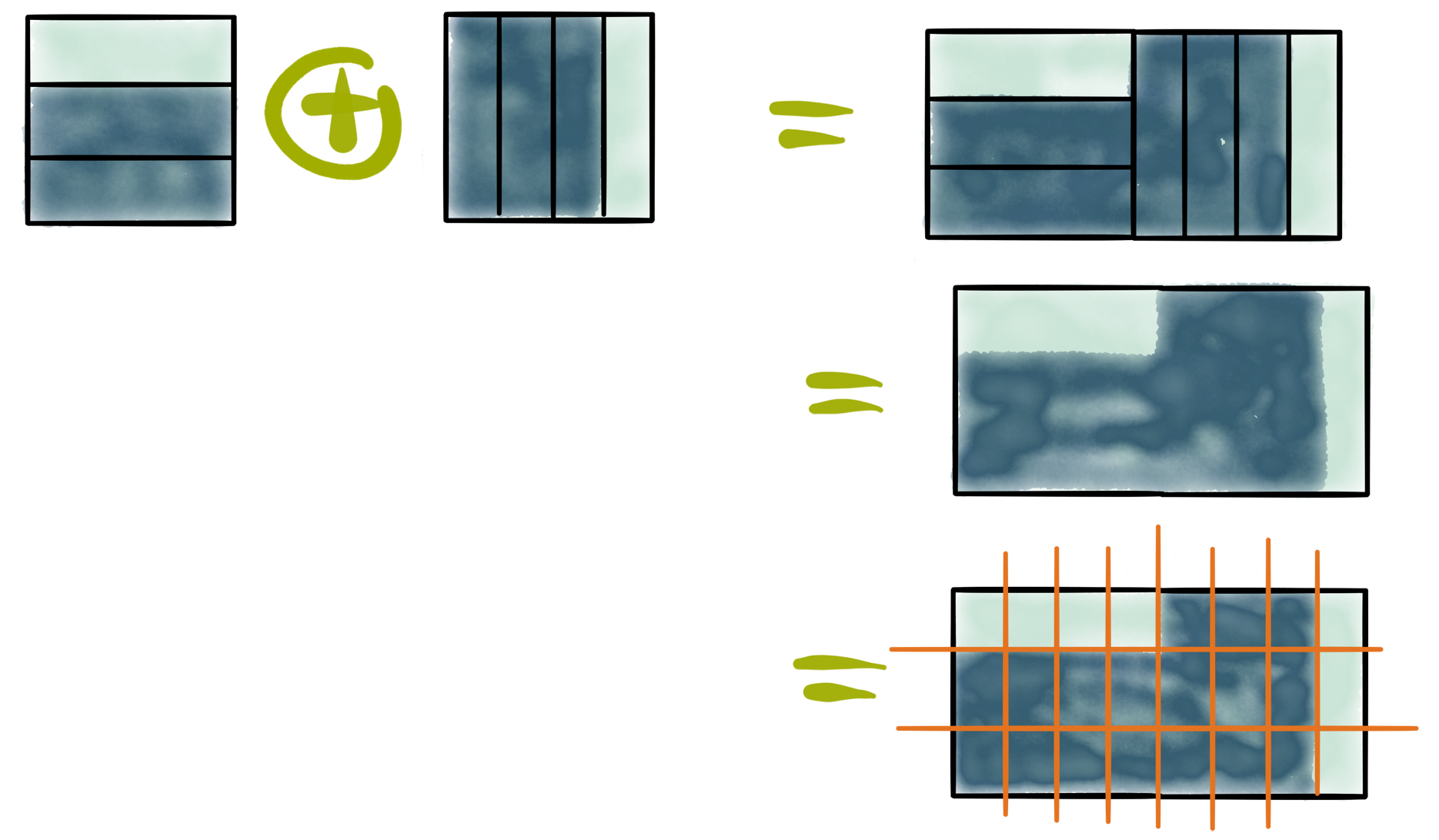
Wenn beide Brüche einfach so zusammengeführt werden, ist die Maßzahl der dunkelblau markierten Fläche, die hier das Salz darstellen soll, zwar tatsächlich gleich $\frac{17}{24}$, aber dieser Bruch kann nicht abgelesen werden, da die Stücke unterschiedlich groß sind. Zunächst müssen also beide Hälften weiter unterteilt werden, bis die gleiche Auflösung entsteht. Dann kann aber die verkürzte Rechnung $\frac{8}{12}\oplus \frac{9}{12} = \frac{17}{24}$ verwendet werden.
Allerdings widerspricht dieses Ergebnis der Beispielanwendung bei Durchschnittsgeschwindigkeiten oben. Dort ist jede Zähler/Nenner-Kombination möglich. Das liegt jedoch daran, dass dort Zähler und Nenner beliebige (nicht-negative) reelle Zahlen sein können und das Konzept von Erweitern und Kürzen keinen Sinn mehr ergibt.
Eine letzte Anwendung der “falschen” Addition, die – im Gegensatz zu den Mischverhältnissen oben – ausschließlich bei vollständig gekürzten Brüchen das richtige Ergebnis liefert, sind Ford-Kreise. Diese stellen eine geometrische Konstruktion mit zahlreichen Anwendungen dar. Hier in diesem Kontext soll es aber nur um deren Definition gehen. Gegeben sei der Zahlstrahl, auf dem alle ganzen Zahlen markiert sind. Über jeder ganzen Zahl wird ein Kreis mit Durchmesser $1$ gezeichnet, sodass dieser den Zahlenstrahl bei der zugehörigen Zahl berührt und ebenso jeden Nachbarkreis.
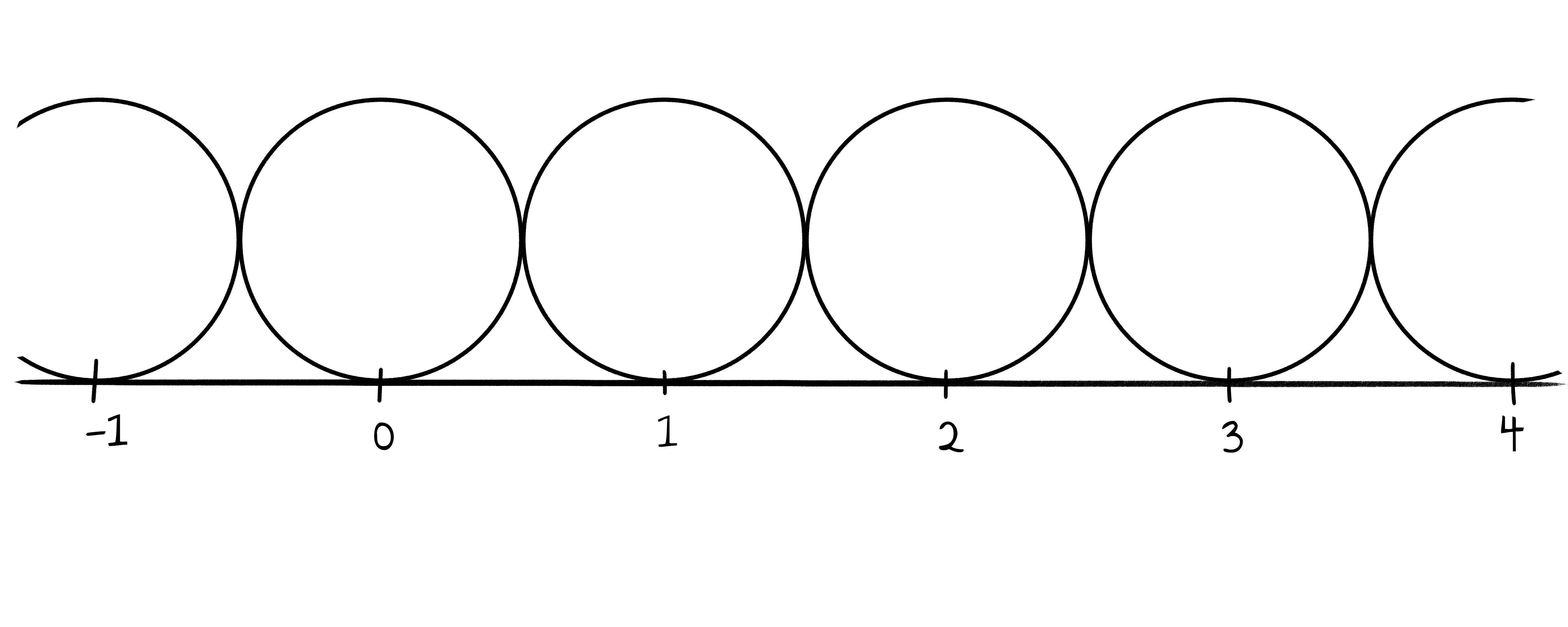
Anschließend wird in jeden Zwischenraum ein weiterer Kreis eingezeichnet, der die beiden Kreise und den Zahlenstrahl berührt. Dieser ist immer eindeutig nach dem Satz von Miquel (Koecher & Krieg, 2007).
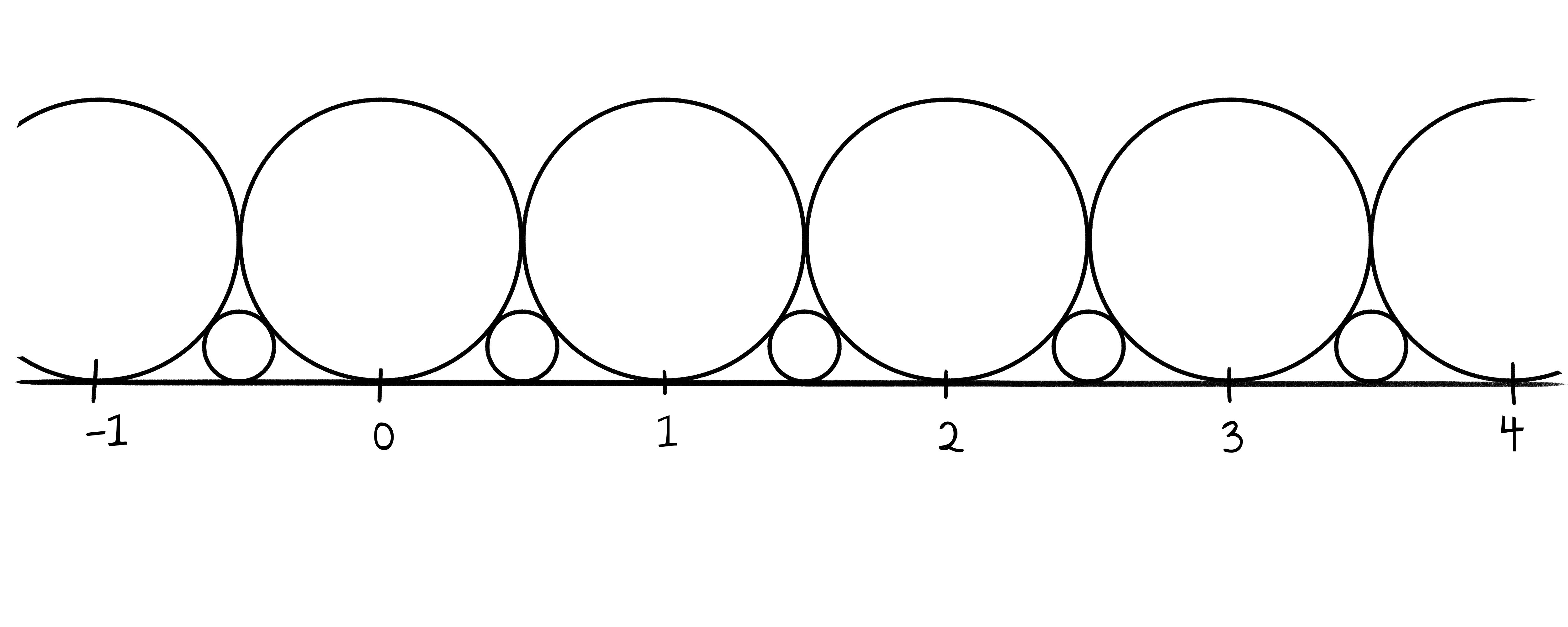
Dieser Vorgang wird anschließend unendlich oft wiederholt.
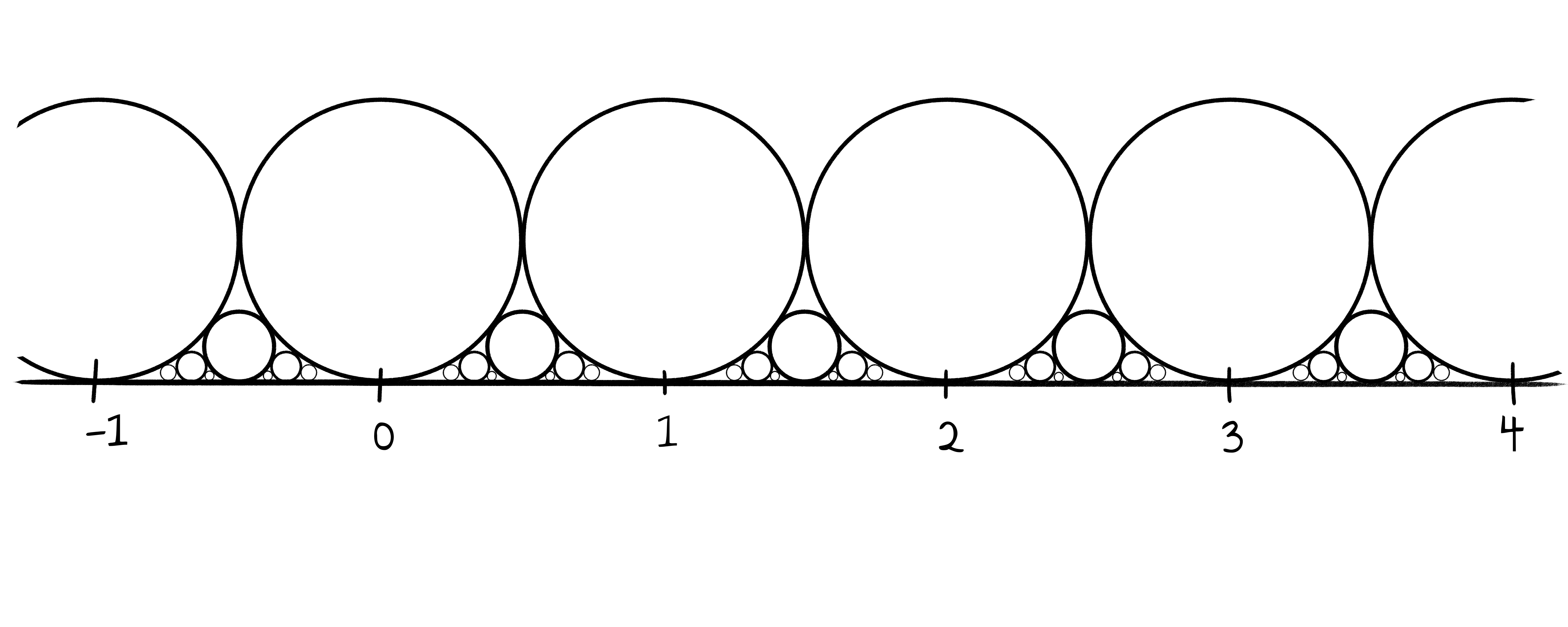
Dann gilt folgender Satz.
Satz: Sind zwei Kreise gegeben, deren Mittelpunkte über den Zahlen $\frac{a}{b}$ und $\frac{c}{d}$ liegen, wobei beide Brüche vollständig gekürzt sein sollen, dann liegt der Mittelpunkt des neuen Kreises zwischen ihnen über der Zahl $\frac{a}{b}\oplus\frac{c}{d}$.
Ein Beweis dieses Satzes hängt hauptsächlich davon ab, wie viel Wissen man über tangentiale Kreise voraussetzen möchte. Hier sei einfach auf den Originalartikel von Lester Ford (1938) verwiesen.
In einfacheren Worten besagt der Satz, dass in der nachfolgenden interaktiven Visualisierung jeder Bruch die $\oplus$-Summe seiner größeren Nachbarn ist.
Anleitung: Stellen Sie am Schieberegler unten den Nenner ein, bis zu dem die entsprechenden Ford-Kreise gezeichnet werden.
Die Folge an Brüchen, die hierbei – von links nach rechts gelesen – entsteht, wird Farey-Folge genannt. Diese besitzt viele interessante Eigenschaften. Für den Kontext des einfachen Bruchrechnens soll die Definition via Ford-Kreise hier aber genügen.
In allen drei Beispielen war also die “falsche” Addition doch die richtige, solange sie im richtigen Kontext auf die richtige Art und Weise angewendet wurde.