Operatives Prinzip
(Krauthausen & Scherer, 2008; Reiss & Hammer, 2013; Wittmann, 1981 & 1985)
Das operative Prinzip beruht auf Piagets Theorie der Operationen, nach der Lernen nur durch eigenes Handeln und als Verinnerlichung von Handlungen geschieht und sich das Denken aus dem Wahrnehmen und Handeln des Kleinkindes entwickelt. Diese Theorie wurde von Aebli zu einem System von Operationen weiterentwickelt. In diesem System geschieht die Konstruktion von Operationen so, dass sie auch allein in der Vorstellung verfügbar sind. Die Organisation der Vorstellungen in Gruppierungen gewährleistet die erwünschte Beweglichkeit des Denkens. Dies bedeutet für den Unterricht, dass mathematische Begriffe und Techniken auf die sie begründenden Handlungen zurückgeführt werden müssen, um sie als Operationen zu verinnerlichen. Beim operativen Üben werden dann vielfältige mentale Beziehungen und Zusammenhänge hergestellt.
Das operative Prinzip umfasst nach Reiss & Hammer (2013, S.74 ff.) drei Aspekte:
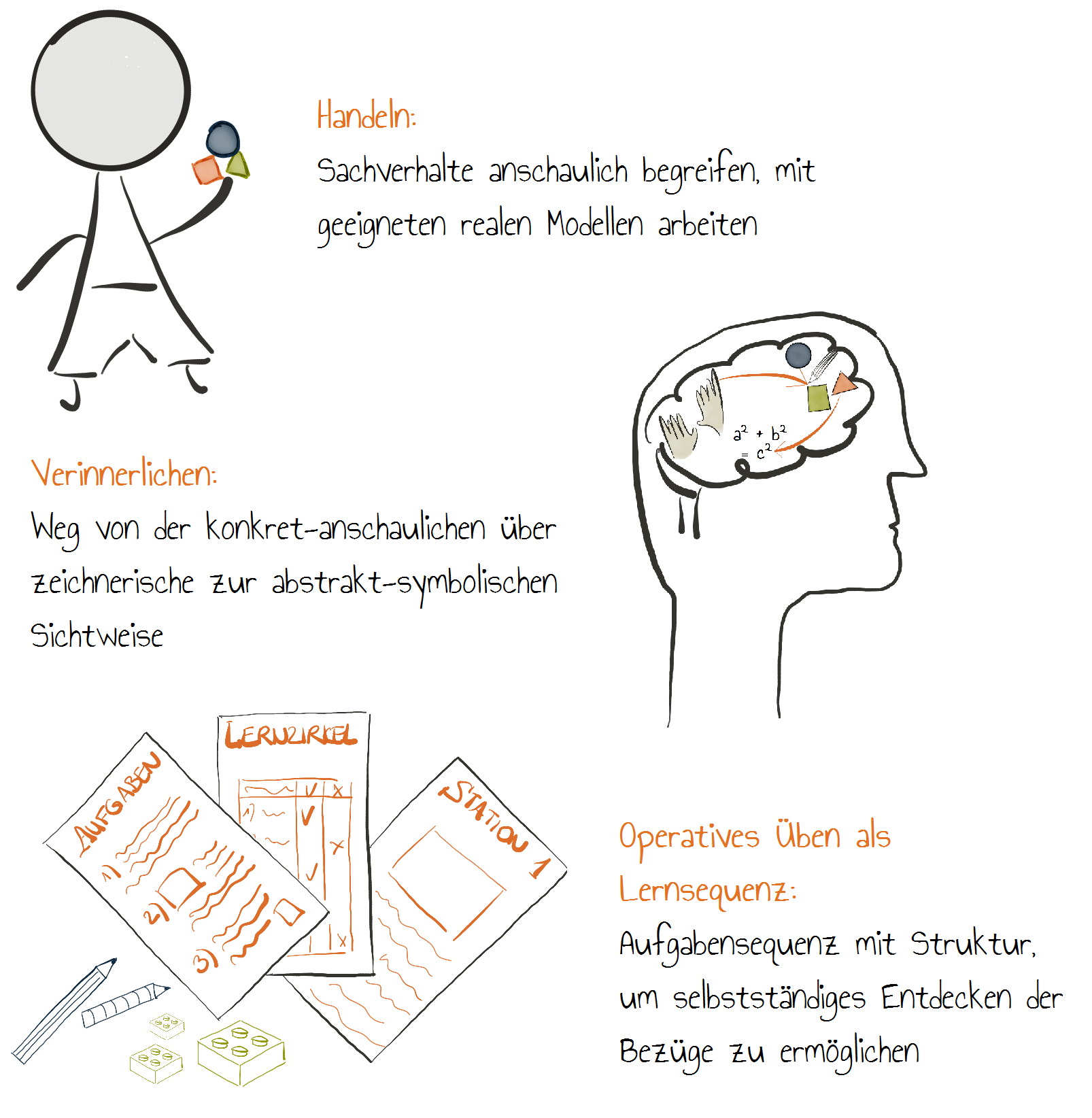
Einige Umsetzungen des operativen Prinzips finden Sie unter Anwenden des operativen Prinzips, ebenso wie Konsequenzen für den Unterricht, die in einem späteren Teil des Moduls besprochen werden.
Beispiele
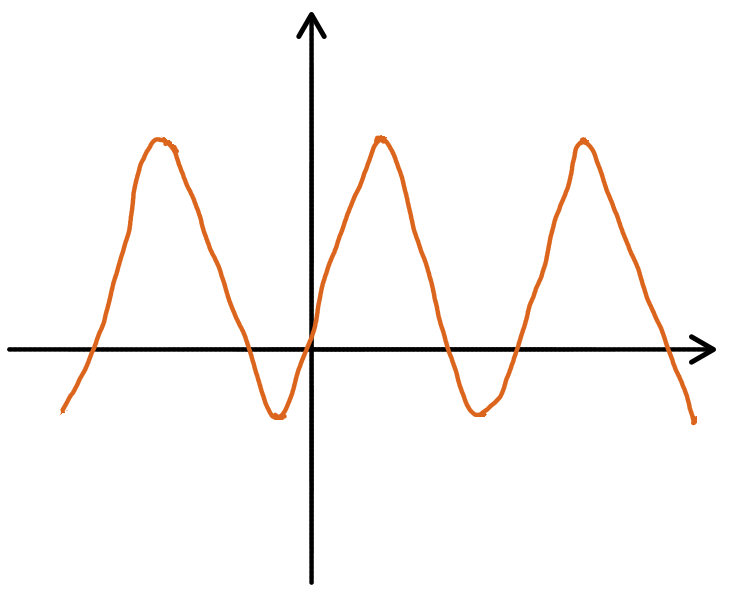
- Zum operativen Üben kann man die folgende Aufgabe benutzen. Wie müssen die Koordinatenachsen beschriftet werden, damit hier die Funktion f(x) = sin (2x) + 0,5 dargestellt wird?
- Bruchzahlen werden mit Hilfe von Papierrechtecken eingeführt. Faltet man ein Rechteck einmal, entstehen zwei Hälften. Faltet man diese noch einmal, entstehen vier Viertel. Der Wert des Bruches ist aber immer 1 (das gesamte Papierrechteck). Damit kann man leicht das Kürzen beziehungsweise das Erweitern veranschaulichen. Haben die Lernenden das Rechteck als reales Modell verstanden, reicht für das Einführen von weiteren Operationen eine Zeichnung des Rechtecks, auf der dann die Faltungen angedeutet werden. Das Ziel ist, dass die Lernenden mit Bruchzahlen sicher umgehen können, da sie das Rechteck als Stütze verinnerlicht haben und mental darauf zurückgreifen können.
- beliebige Objekte mit Spiegel verdoppeln (Objekte: Plättchen vor dem Spiegel, im Spiegel und Gesamtanzahl; Operationen: Verschieben des Spiegels; Wirkung: Wie ändert sich die Anzahl der Plättchen?)
- „Was-wäre-wenn“ Aufgaben (primär nicht die Formeln verwenden, sondern Zusammenhänge sehen und spezifische Rolle von Variablen verstehen)
- Neue Rechenwege werden mit verschiedenen Lernmitteln ausprobiert, dabei Gemeinsamkeiten und Unterschiede bezüglich der Lösungswege/Gesetze erkennen und nutzen
- In Szene 3: Erarbeitung der Funktionseigenschaften in Zweiergruppen - Teil 2 sehen wir ab 2:33 min eine Arbeitsgruppe, die die Bedeutung der Variablen in einer operativen Übungsphase erkundet.