Themen zum Weiterdenken und Knobeln
Nachdem bei den Lernenden der Begriff der Dreieckszahlen gefestigt ist und sie eine Grundvorstellung entwickelt haben, kann im Unterricht auf dem vorhandenen Wissen aufgebaut werden. Eine sehr anschauliche Darstellung für die Dreieckszahlen sind unsere Zählsteine. Nun könnte eine mögliche Aufgabenstellung lauten:
Wichtig hierbei, zuerst sollte diskutiert werden, was Tetraederzahlen sind und wie diese ussehen. Den Schülerinnen und Schülern sollte bewusst werden, dass das Tetraeder eine dreidimensionale Figur ist, das Dreieck jedoch nur zweidimensional.
Um diese räumliche Darstellung etwas zu vereinfachen, können mit den Schülerinnen und Schülern im Steine gesammelt werden oder Tennisbälle organisiert werden. Natürlich gibt es noch viele weitere Hilfsmittel, die einer Visualisierung dienen. Nachdem die Schülerinnen und Schüler etwas geknobelt haben, sollte eine richtige Darstellung vom Lehrenden präsentiert werden, um alle auf den gleichen Stand zu bringen und die nächste Aufgabe bearbeiten zu können.
Tipps für die Lernenden:
- Bezug zu Dreieckszahlen
- Welche Rechenoperation versteckt sich hinter der Berechnung von Dreieckszahlen?
- Erstellen einer Tabelle um evtl. ein Schema zu erkennen
Das Pascalsche Dreieck
Wir konstruieren ein Dreieck aus Zahlen, wobei die Spitze eine 1 ist und die von der Spitze ausgehenden Schenkel auch nur aus Einsen bestehen. Die dazwischen liegenden Zahlen erhalten wir aus der Summe der beiden darüber liegenden Zahlen.
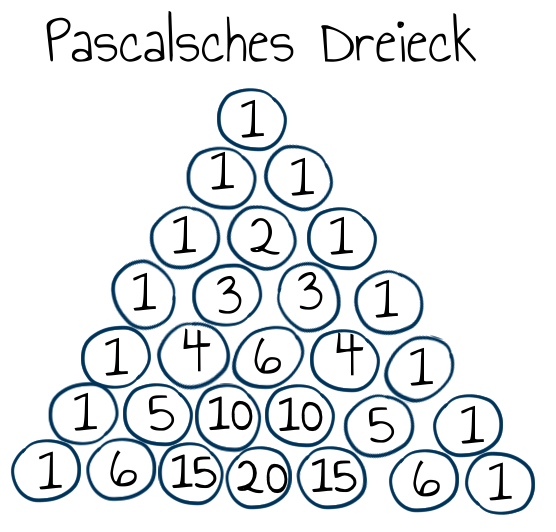
Zusammenhänge im Pascalschen Dreieck
1. Dreieckszahlen
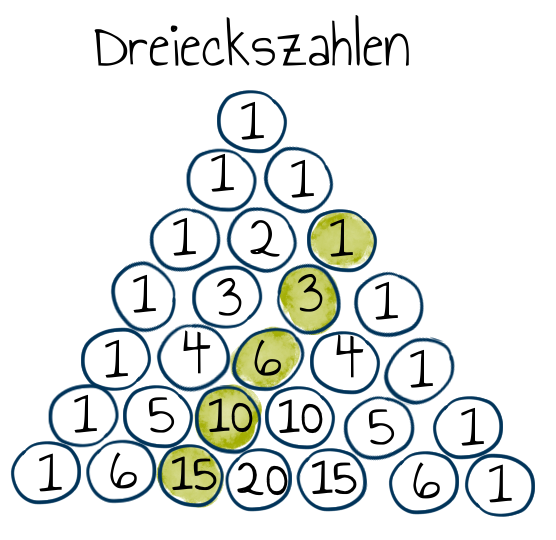
Das Pascalsche Dreieck eignet sich hervorragend, um einen Überblick der ersten Dreieckszahlen zu bekommen. Wir können die Folge der Dreieckszahlen ganz einfach in der 2. Diagonalen ablesen, wobei mit der Nummerierung der Spalten an der Spitze mit 0 begonnen wird.
2. Tetraederzahlen
Man kann die Folge der Tetraederzahlen direkt aus dem Pascalschen Dreieck ablesen. Dazu betrachten wir die 3. Diagonale und erhalten die gesuchte Folge.
3. allgemeine binomische Formel
Hier ist ein Bezug zur Mittelstufe möglich, denn zu diesem Zeitpunkt lernen Schülerinnen und Schüler die binomische Formel $(a+b)^2=a^2+2ab+b^2$ kennen. Allgemein lautet diese Formel
\[(a+b)^n = \sum_{i=0}^n\binom{n}{i} a^i b^{n-i}.\]
D.h. die Lernenden werden nur mit einem speziellen Fall, $n=2$ vertraut gemacht. Doch wie lösen wir allgemeine binomische Formel, sodass wir die richtigen Koeffizienten erhalten? Die Lösung ist, wir können die gesuchten Koeffizienten für die Formel $n$-ten Grades in der $n$-ten Zeile ablesen.

Beispiele
Für $n=3$ gilt: $(a+b)^3=a^3+3a^2b+3ab^2+b^3$
Für $n=4$ gilt: $(a+b)^4=a^4+4a^3b+6a^2b^2+4ab^3+b^4$
Für $n=5$ gilt: $(a+b)^5=a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5$
$ \vdots $
4. Fibonacci-Folge
Hierfür müssen die Fibonacci-Zahlen noch kurz eingeführt werden, dem Mathematikstudenten sind diese schon bekannt. Die Fibonacci-Zahlen sind eine der berühmtesten Zahlenfolgen der Welt und genau deshalb sollte jede Schülerin und jeder Schüler einmal etwas von diesen Zahlen gehört haben. Die ersten beiden Folgenglieder sind durch 1 und 1 definiert. Wir erhalten die weiteren Folgeglieder, indem wir die beiden vorherigen addieren. Das heißt die $n$-te Fibonacci-Zahl $f_n$ berechnet sich allgemein durch
\[f_n=f_{n-2}+f_{n-1}\]
Es ergibt sich die Folge
\[0,1,1,2,3,5,8,13,21,34,55,89…\]
Der interessante Zusammenhang zum Pascalschen Dreieck ist nun, dass die $n$-te Fibonacci-Zahl als Summer der $(n-1)$-ten “flachen” Diagonalen wiederzufinden ist. Diese entstehen, wenn man von Zeile $a$, Position $b$ zu Zeile $a+1$, Position $b-1$ geht; sofern das möglich ist.
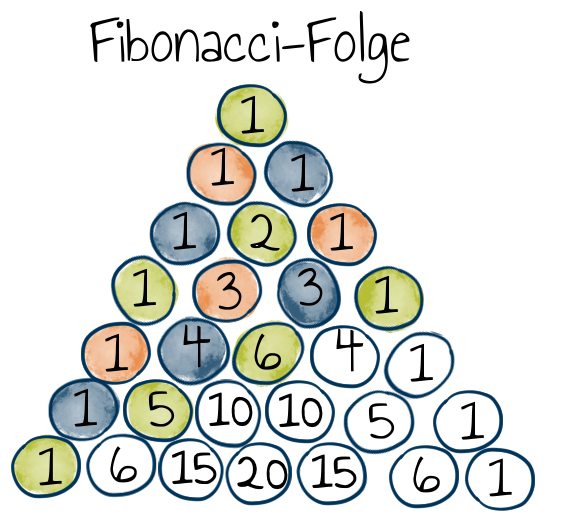
Eine Möglichkeit dieses Thema im Unterricht zu behandeln ist, den Lernenden die Fibonacci-Folge an der Tafel anzugeben mit der Aufgabe, das Muster hinter der Zahlenfolge zu erkennen.
Möchte man jedoch, dass die Schülerinnen und Schüler die Fibonacci-Folge selbst entdecken, so kann man ihnen diese bekannte Aufgabe stellen.
5. Binomialkoeffizienten
Der Begriff des Binomialkoeffizienten ist den Lernenden erst ab der Oberstufe vertraut, somit bietet sich dieser Zusammenhang gut in einem W-Seminar an, um Bezug zum aktuellen Unterrichtsgeschehen zu schaffen. Wir können die Binomialkoeffizienten aus dem Pascalschen Dreieck ablesen. $\binom{n}{k}$ finden wir als $(k+1)$-ten der $(n+1)$-ten Zeile.
