Zusammenhang zentrierte Quadratzahlen und Dreieckszahlen

Erster Zusammenhang

Zwischen den auf den ersten Blick scheinbar unabhängigen Dreiecks- und zentrierten Quadratzahlen gibt es einen Zusammenhang. Es gilt: Die $n$-te zentrierte Quadratzahl $q_n$ ist um eins größer als das vierfache der $n$-ten Dreieckszahl. Als Formel festgehalten ergibt sich

\[q_n=1+4D_n.\]

Durch Umformulieren kann dies gezeigt werden.

\[q_n=n^2+(n+1)^2=2n^2+2n+1=2n(n+1)+1=1+4\cdot \frac{n(n+1)}{2}=1+4D_n\]

Als Beispiel soll die dritte zentrierte Quadratzahl betrachtet werden.

\[q_3=3^2+4^2=\]

\[=1+24=1+4\cdot 6=\]

\[=1+4D_3.\]

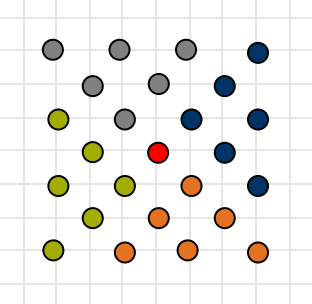
Die visuelle Überlegung ist wie folgt: Es gibt die Startkugel in der Mitte, hier in Rot und außen herum wird viermal die dritte Dreieckszahl gelegt, hier in Blau, Orange, Grün und Grau.

Zweiter Zusammenhang

Ebenso bemerkenswert ist folgende Verknüpfung. Jede zentrierte Quadratzahl $q_n$ lässt sich durch eine bestimmte Summe von Dreieckszahlen darstellen. Um genau zu sein werden jeweils drei Folgeglieder der Dreieckszahlen genutzt:

\[q_n=D_{n-1}+2\cdot D_n+D_{n+1}=\frac{(n-1)n}{2}+n(n+1)+\frac{(n+1)(n+2)}{2}\]

Am Beispiel der dritten zentrierten Quadratzahl:

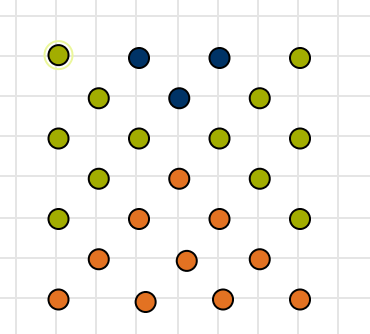
Die unten stehende Grafik zeigt erneut $q_3$ in drei Farben. Das kleinste Dreieck in Blau entspricht $D_2$, die beiden grünen entsprechen $D_3$ und das orange $D_4$, wodurch

\[q_3=D_2+2D_3+D_4= 3+2\cdot 6+10=25.\]

gilt.

Verallgemeinerung

Die Überschrift verrät bereits, dass Dreieckszahlen wohl mit zentrierten Zahlen im Allgemeinen in Verbindung stehen. Dasselbe Bild kann also auch für andere zentrierte Zahlen hergestellt werden.

Betrachtet man Fünfecks- oder Sechseckszahlen:

Links im Bild ist das zentrierte Fünfeck zu sehen, das aus Dreieckszahlen zusammengesetzt wird. In der Mitte befindet sich eine einzelne Kugel in Rot. Außen, um die Kugel herum, finden wir fünf Dreieckszahlen derselben Größe. Rechts im Bild ist das zentrierte Sechseck zu sehen, welches ein Dreieck mehr aufzeigt. Dies führt zu folgender Vermutung:

\[Z_{k,n}=1+k\frac{n(n+1)}{2}\]

Wobei $Z_{k,n}$ die $n$-te zentrierte $k$-Eckszahl beschreibt.