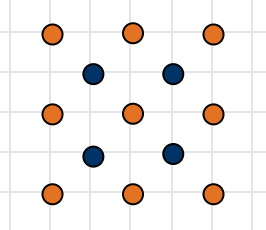
Zentrierte Quadratzahlen

Addieren von zwei aufeinanderfolgende Quadratzahlen, liefert eine zentrierte Quadratzahl. Sie gehören den zentrierten Polygonalzahlen an.

Der Summenwert muss allerdings nicht zwangsläufig auch eine Quadratzahl sein. Allgemein lässt sich eine beliebige zentrierte Quadratzahl $q_n$ wie folgt berechnen:

\[q_n=Q_n+Q_{n+1}, n\in\mathbb{N}, n>1\]

Einsetzen der bekannten Formeln liefert:

\[q_n=Q_n+Q_{n+1}=n^2+(n+1)^2=2 n^2+2n+1\]

Die ersten zentrierten Quadratzahlen lauten:

\[q_0=2 \cdot 0^2+2 \cdot 0+1=1=1^2+0^2\]

\[q_1=2 \cdot 1^2+2 \cdot 1+1=5=2^2+1^2\]

\[q_2=2 \cdot 2^2+2 \cdot 2+1=13=3^2+2^2\]

\[q_3=2 \cdot 3^2+2 \cdot 3+1=25=4^2+3^2\]

\[ \vdots\]

Um die zentrale Kugel wird jeweils ein Polynom gelegt, wobei die Seitenlänge des Polynoms jeweils um eine Kugel vergrößert wird.

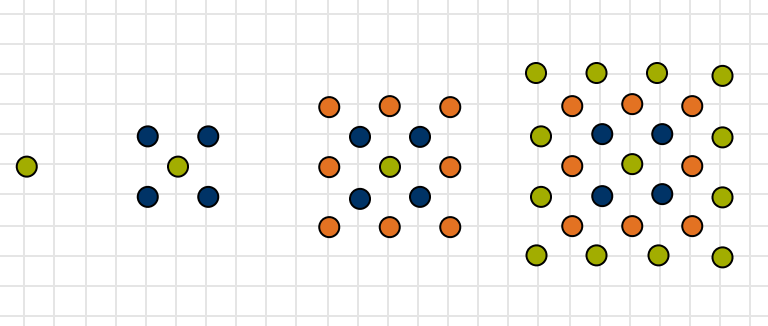
Die zweite zentrierte Quadratzahl wird korrekterweise bei zwei aufeinanderfolgende Quadratzahlen mit zwei Farben dargestellt, mit $q_2=Q_2+Q_3=2^2+3^2=9+4$.