Definition
Eine Quadratzahl entsteht, indem eine ganze Zahl mit sich selbst multipliziert wird, wie zu Beginn die $36$ betrachtet wurde. Beispielsweise ist die $81=9\cdot 9=9^2$ ebenfalls eine Quadratzahl.
Quadratzahlen $Q_1, Q_2, …, Q_n, n\in\mathbb{N}$ kann man sich als quadratisches Punktegitter vorstellen. Nachfolgende interaktive Visualisierung zeigt die Quadratzahlen von $0$ bis $25$.
Anleitung: Den grünen Schieberegler in der Leiste hin und her bewegen.
Allgemein gilt für alle $n\in\mathbb N$:
\[Q_n = n^2.\]
Also,
\[Q_1=1^2 = 1\]
\[Q_2 = 2^2=4\]
\[Q_3= 3^2=9\]
\[Q_4= 4^2=16\]
\[ \vdots \]
Je nach Autor wird die $0$ als mögicher Index ein- bzw. ausgeschlossen.
Wird ein Quadrat $Q_n$ um $2n+1$ Kugeln vergrößert – also um die orangenen Kugeln im Bild unten – entsteht das neue Quadrat $Q_{n+1}$, somit ist
\[Q_{n+1}=Q_{n}+2n+1\]
Anleitung: Den grünen Schieberegler in der Leiste hin und her bewegen. Oben die Art der Generierung auswählen durch Klick auf das entsprechende Piktogramm.
Dieses Ergebnis lässt sich auch direkt mit einer binomischen Formel bestimmen:
\[(n+1)^2=n^2+2n+1\]
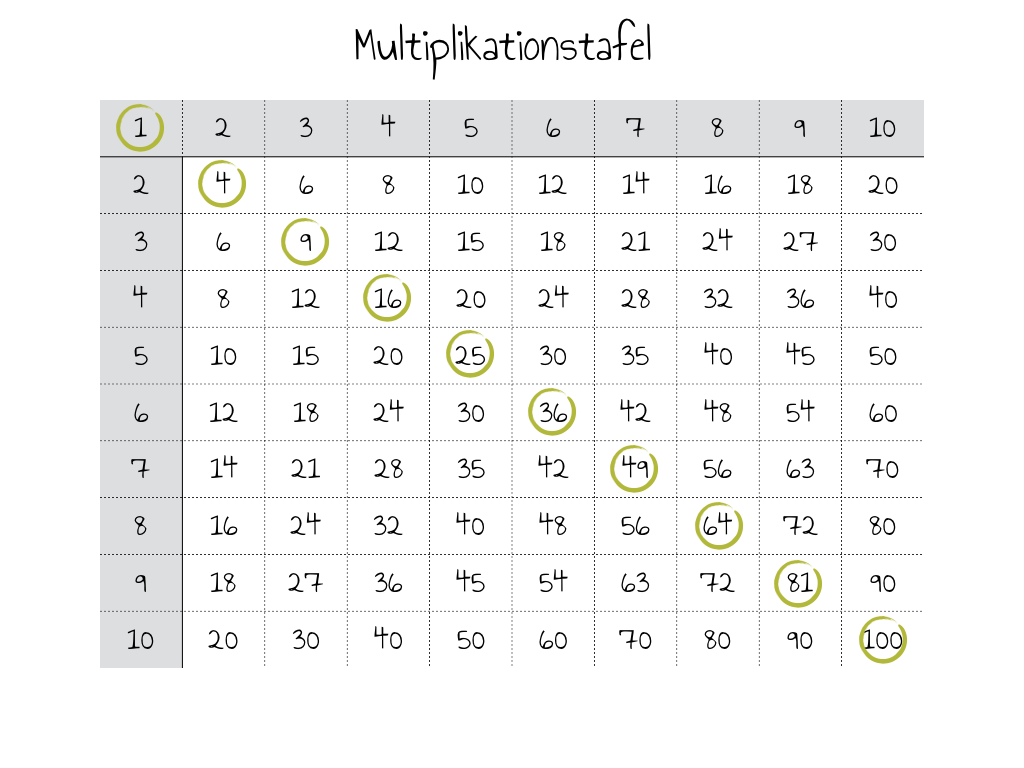
Und in einer Multiplikationstafel sind die Quadratzahlen genau auf der Diagonalen zu finden: