Fachwissenschaft Mathematik: Überblick

Dieser Abschnitt richtet sich an Lehrende, welche Anregungen suchen, selbst Aufgaben zur Satzgruppe des Pythagoras zu erstellen. Neben den Standardberechnungen, die aus der Schule bekannt sind, möchten wir exemplarisch auch auf Aufgaben eingehen, die die kognitive Aktivierung der Lernenden mehr anregen. Beispielsweise könnten Sie den Lernenden eine Bastelaufgabe geben und sie hierdurch zum gemeinsamen Überlegen, Diskutieren und Verstehen animieren.

In der Mathematik ist die Berechnung einer Streckenlänge eine der häufigsten Anwendungen, was die herausragende Rolle des Satzes des Pythagoras bestätigt. Durch diese Erkenntnis eröffnen sich insbesondere für den Geometrieunterricht neue Möglichkeiten.

Zum Satz des Pythagoras existieren bereits unzählige Aufgabensammlungen, weshalb dieses Kapitel kurz gehalten wird. Für weitere Anregungen können Sie Schulbücher, wie beispielsweise Diestel und Feuerlein (2007) oder Fraedrich (1995) heranziehen.

Begonnen wird mit einer Art kleinen Formelsammlung mit Formeln, welche im rechtwinkligen Dreieck gelten. Im folgenden Kapitel finden Sie ausgewählte Aufgaben zum Satz des Pythagoras.

Typische Aufgabenstellungen

Zu den typischen Aufgabenstellungen im rechtwinkligen Dreieck zählt die Berechnung einer Strecke. Hierzu soll eine kleine Formelsammlung beschrieben werden. Diese soll zum selbständigen Entwickeln von Aufgaben anregen. Auf der nächsten Seite finden Sie hierzu noch konkrete Beispielaufgaben.

Kleine Formelsammlung

Anfangs die bereits erarbeiteten Größen:

Mit dem Satz des Pythagoras:

• $a= \sqrt{c^2-b^2}$
• $b= \sqrt{c^2-a^2}$
• $c= \sqrt{a^2+b^2}$

Mit dem Kathetensatz:

• $a= \sqrt{cp}$
• $b= \sqrt{cq}$

Mit dem Höhensatz:

• $h= \sqrt{pq}$

Weitere Streckenberechnungen im Dreieck können beispielsweise sein:

Die Höhen:

• $h_a=b$
• $h_b=a$
• $h_c=\frac{ab}{c}$

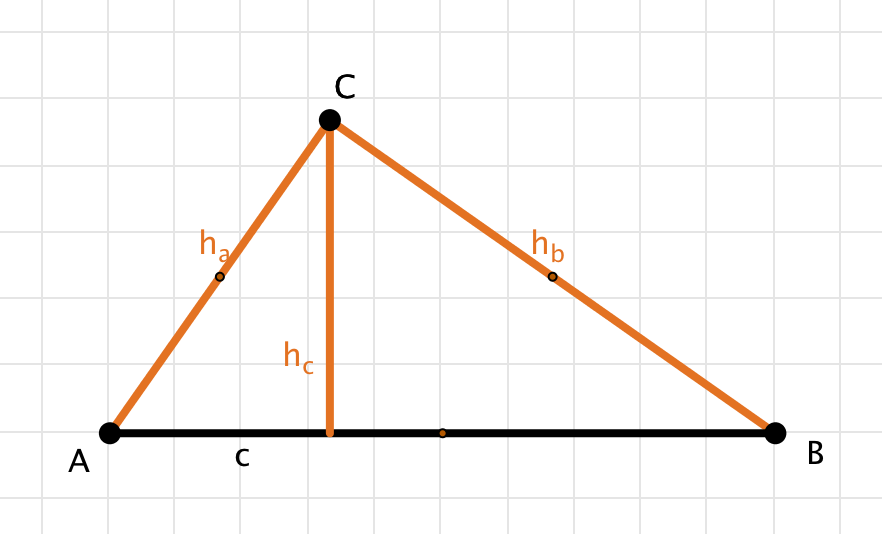
Die Mittelsenkrechten:

• $m_a=\frac{b}{2}$
• $m_b=\frac{a}{2}$
• $m_c=\frac{bc}{2a}$

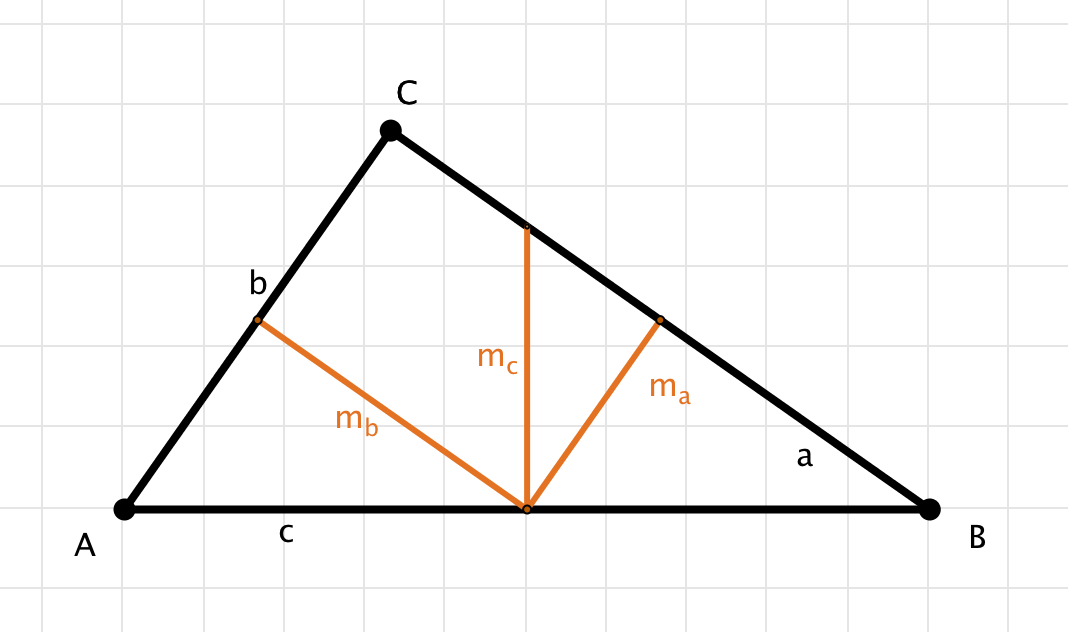
Die Seitenhalbierenden:

• $s_a=\frac{\sqrt{a^2+4b^2}}{2}=\frac{\sqrt{3b^2+c^2}}{2}$
• $s_b=\frac{\sqrt{4a^2+b^2}}{2}=\frac{\sqrt{3a^2+c^2}}{2}$
• $s_c=\frac{c}{2}$

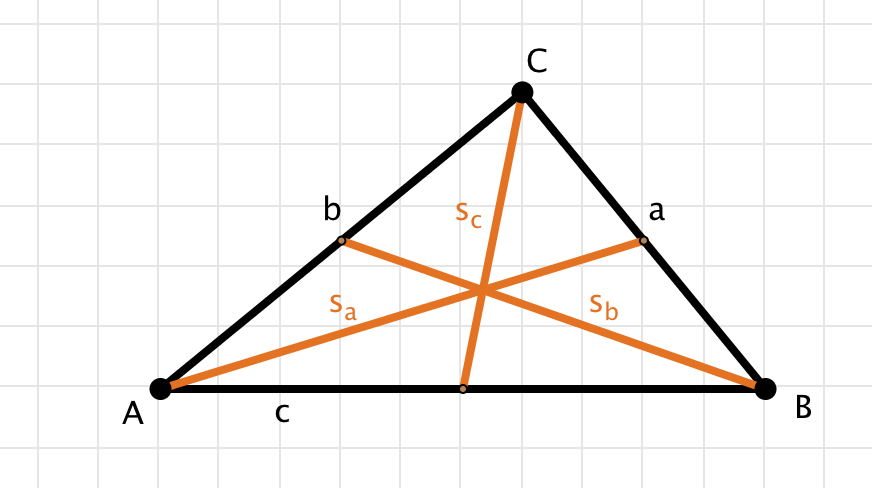
Die Winkelhalbierenden (siehe Grafik unten):

• $w_a=b \frac{\sqrt{2c}}{\sqrt{b+c}}$
• $w_b= a \frac{\sqrt{2c}}{\sqrt{a+c}}$
• $w_c=ab \frac{\sqrt{2}}{a+b}$

Zusätzlich können auch verschiedene Radien mit einbezogen werden, beispielsweise der Umkreisradius oder Inkreisradius.

• Umkreisradius: $ R= \frac{c}{2}$
• Inkreisradius: $ r= \frac{a+b-c}{2}$

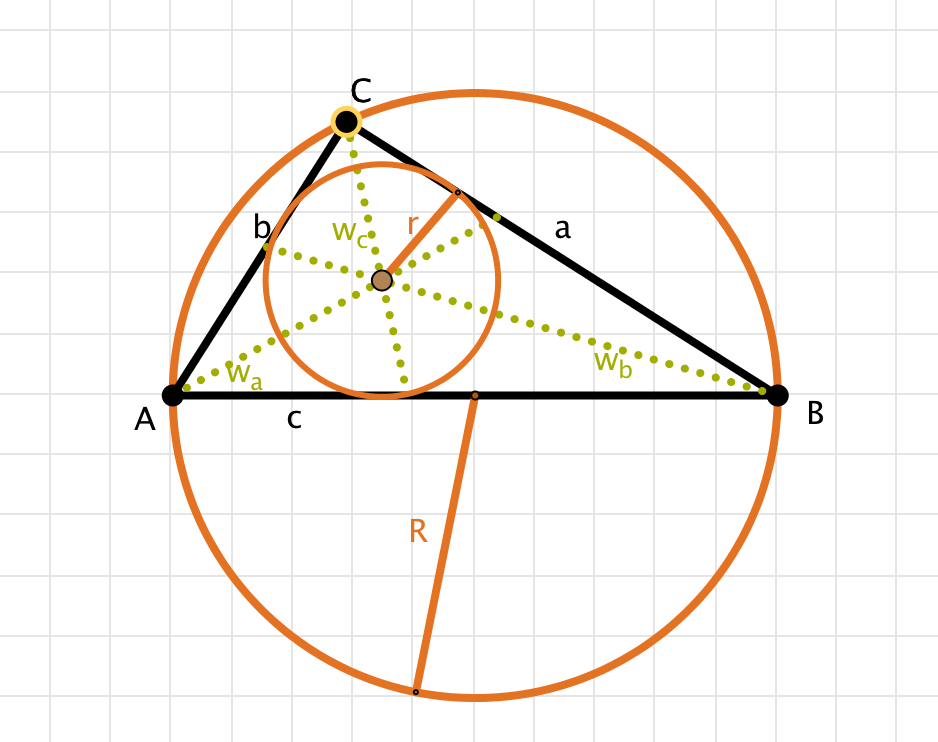
Mögliche Aufgabenstellungen

Nach Einführung der Satzgruppe können verschiedene Aufgaben gestellt werden. Hierbei ist jeweils eine der Seiten unbekannt und mindestens zwei andere Seiten gegeben.

Beispielsweise:

1. Gegeben sei ein rechtwinkliges Dreieck mit Kathetenlängen $a, b$. Berechne $c$.
2. Gegeben sei eine Kathete und die Hypotenuse. Berechne die unbekannte Kathetenlänge.
3. Gegeben sei ein rechtwinkliges Dreieck mit Höhe $h$ und Hypotenusenabschnitt $p$. Gesucht seien die Größen/eine der folgenden Größen: $a, b, c, q$

Bei Einführung der Satzgruppe werden typischerweise konkrete Werte für die Seiten angegeben. Weiterführend können zum Beispiel Termumformungen etc. angewandt werden und zu ganzzahligen Lösungen übergegangen und somit auf die pythagoreischen Zahlentripel eingegangen werden.

Beweisaufgaben

Von den gegebenen Formeln kann ebenfalls auf Beweisaufgaben übergegangen werden und somit das Schwierigkeitsniveau erhöht werden. Insbesondere können in rechtwinkligen Dreiecken viele weitere Größen durch die Seitenlängen ausgedrückt werden. Das erlaubt Aufgaben der folgenden Art:

Zeige, dass im rechtwinkligen Dreieck mit Katheten $a,b$ und Hypotenuse $c$ der Inkreisradius gleich $\frac{a+b-c}{2}$ ist.