Fachwissenschaft Mathematik: Aufgaben

Toolbox Lehrerbildung
Department of Educational Science
TUM School of Social Sciences and Technology
Technische Universität München

Fachwissenschaft Mathematik: Aufgaben

Im Unterrichtsvideo in Szene 6: Besprechung der Hausaufgabe gibt die Lehrerin den Schülerinnen und Schülern ein Übungsblatt.

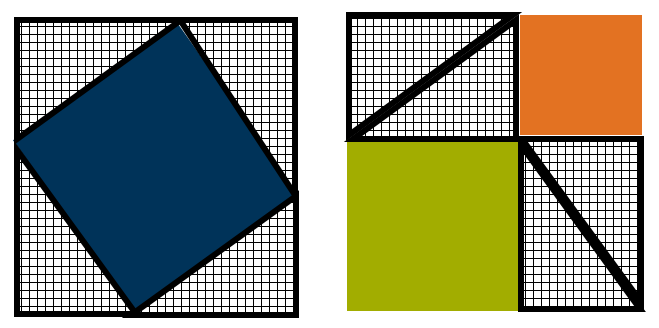
Der Pythagorasbaum in Aufgabe 3 beispielsweise ist eine gute Aufgabe um abstrahiert von der Formel die Zusammenhänge zu verstehen.

In diesem Abschnitt wollen wir einige Übungsaufgaben zur Verfügung stellen. Hierbei liegt der Fokus auf dem Rechnen und dem analytischen Vorgehen. Es soll gezeigt werden, dass mit einer eigentlich leichten Formel, wie der des Satzes des Pythagoras, bereits eine Vielzahl von größeren und schweren Problemen gelöst werden kann. Bei manchen Aufgaben finden sich Lösungen am Ende, um das Ergebnis zu verifizieren. Als letzte Aufgabe stellen wir auch noch ein geometrisches Spiel vor, bei dem der Zusammenhang zwischen Analytik und Geometrie hergestellt wird.

Aufgabe 1: Allgemeine Abstandsbestimmung

Wir wollen uns hier überlegen, wie der Satz des Pythagoras genutzt werden kann, um Abstände zu berechnen.

(a) Wir starten im $\mathbb{R}^2$. Gegeben sind die Punkte $A=(1,2)$ und $B=(3,3)$. Machen Sie sich eine Skizze und berechnen Sie den Abstand von $A$ nach $B$ mithilfe des Satzes.

Die Lösung lautet $\sqrt{(3-1)^2+(3-2)^2}=\sqrt{6}$.

(b) Wir betrachten nun den $\mathbb{R}^3$. Versuchen Sie das Verfahren aus Teil (a) zu verallgemeinern, um den Abstand von Punkten im dreidimensionalen Raum zu berechnen. Machen Sie sich eine geeignete Skizze mit den Punkten $A=(2,0,0)$ und $B=(3,3,1).$ Gesucht ist die Streckenlänge $\vert AB\vert$. Berechnen Sie dazu zuerst Hilfspunkte $C$ und $D$, bei denen zwei der drei Koordinaten mit $A$ beziehungsweise $B$ übereinstimmen. Wenden Sie danach zweimal den Satz des Pythagoras an, um die Streckenlänge $\vert AB\vert$ zu berechnen.

Wir setzen $C=(B_x,A_y,A_z)=(3,0,0)$ und $D=(B_x,B_y,A_z)= (3,3,0)$. Dann bilden die Punkte $A,B,C$ ein rechtwinkliges Dreieck und es gilt $$\vert AC\vert =\sqrt{\vert AC\vert^2+\vert CD\vert^2}=\sqrt{1^2+3^2}=\sqrt{10}$$. Die Punkte $A,D,B$ bilden auch ein rechtwinkliges Dreieck und es gilt $$\vert AB\vert =\sqrt{\vert AC\vert^2+\vert BD\vert^2}=\sqrt{10+3^2}=\sqrt{19}$$.

Sei $x,y \in\mathbb{R}^n$ dann ist der Abstand von $x$ zu $y$ gegeben durch $$\|x-y\|=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+...+(x_n-y_n)^2}.$$

Aufgabe 2: Konkrete Abstandsbestimmung

In vielen praktischen Situationen können Abstände oft dadurch bestimmt werden, indem man rechtwinklige Dreiecke findet. Ein einfaches Beispiel hierfür:

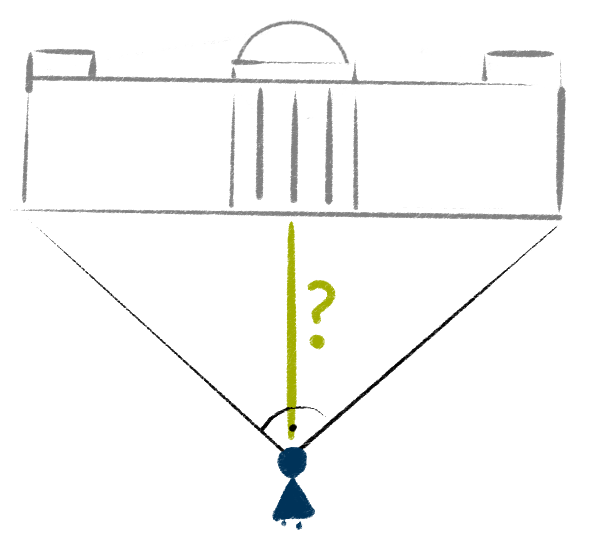
Angenommen, eine Person möchte das $137\,m$ breite Reichstagsgebäude fotografieren. Wie weit muss sie von ihm entfernt stehen, wenn

sie es in ganzer Breite auf das Bild bekommen möchte,
es frontal zu sehen sein soll und
der Öffnungswinkel des Kameraobjektivs genau $90^\circ$ beträgt?

Skizze des Reichstags

Die Vorderseite des Reichstagsgebäudes als Hypotenuse $c$ bildet mit der Kamera als gegenüberliegende Ecke ein rechtwinkliges Dreieck. Dann ist der gesuchte Abstand die Hypotenusenhöhe $h$. Dass das Gebäude frontal zu sehen sein soll, bedeutet, dass dieses Dreieck zudem gleichschenklig ist. In diesem Fall gilt $h=\frac{c}{2} = 68,\!5\,m.$ Diese Formel kann man kennen oder sich leicht geometrisch herleiten (z.b. an einem Quadrat). Eine mögliche Rechnung, die nur die bekannten Varianten des Satzes des Pythagoras verwendet, sieht wie folgt aus: Sei $a$ die Länge der Katheten. Dann sagt der Satz des Pythagoras, dass $2a^2=c^2$ gilt. Der inverse Satz des Pythagoras sagt zudem, dass $\frac{2}{a^2} = \frac{1}{h^2}$. Löst man die zweite Gleichung nach $a^2$ auf und setzt in die erste ein, erhält man $4h^2 = c^2$, was dann anschließend direkt zu obiger Lösungsformel führt.

Aufgabe 3: Geometrische Konstruktion von Wurzeln

In dieser Aufgabe soll gezeigt werden, dass es möglich ist Wurzellängen geometrisch zu konstruieren.

Wir starten mit einer Strecke der Seitenlänge $1$. Die Aufgabe ist es, daraus eine Strecke mit Länge $\sqrt{8}$ zu konstruieren. Die Idee dabei ist, den Term $n+1$ einmal als $\sqrt{n+1}^2$ zu schreiben und einmal als $\sqrt{n}^2 + 1$. Damit gilt

\[\sqrt{n+1}^2=\sqrt{n}^2+1^2\]

und der Satz des Pythagoras garantiert dann, dass ein rechtwinkliges Dreieck mit den entsprechenden Seitenlängen existiert. Diese Idee benutzen wir, um Strecken der Länge $\sqrt{n}$ zu konstruieren. Dazu gehen wir wie folgt vor:

Wir starten mit einer Strecke $\overline{AB}$ der Länge eins, diese dürfen wir mit dem Lineal eintragen.
Wir konstruieren eine Strecke der Länge eins, welche senkrecht auf $B$ steht. Der Endpunkt sei $C$.
Die Strecke $\overline{AC}$ hat nun die Länge $\sqrt2$.
Mit der neuen Strecke kann man dasselbe nochmal machen und wir erhalten die Strecke $\sqrt3$ usw.

Aufgabe 4: Cosinussatz für nicht rechtwinklige Dreiecke

Es seien die beiden Längen $b$ und $c$, sowie der Winkel $\alpha$ bekannt. Ziel ist es die Länge der Seite $a$ zu bestimmen.

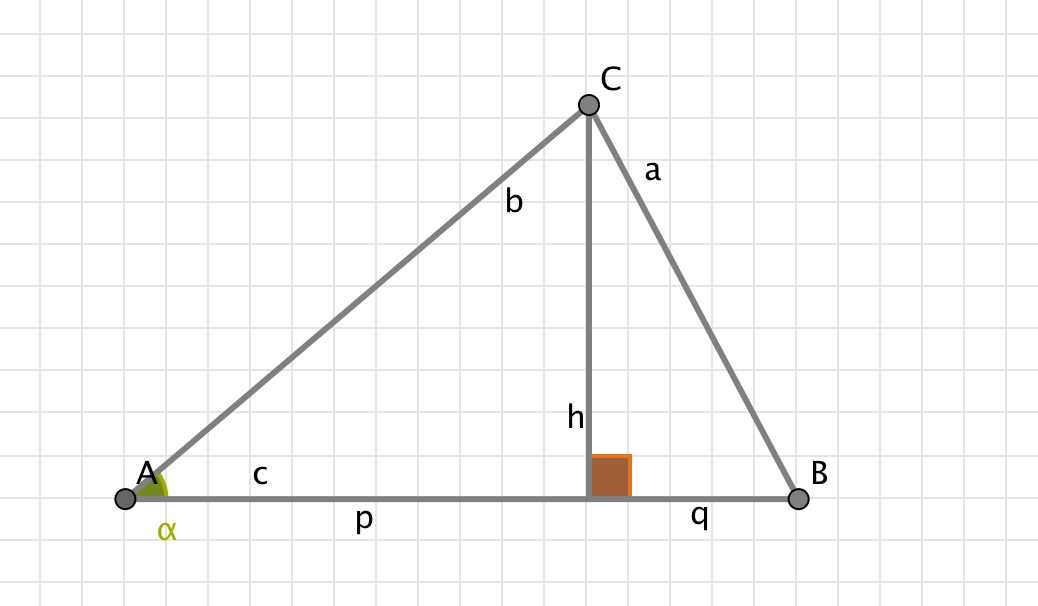
Cosinussatz für nicht rechtwinklige Dreiecke

Hierzu wollen wir nun eine Formel herleiten, die für allgemeine Dreiecke gilt. Das heißt, wenn wir zwei Seitenlängen und einen Winkel kennen soll uns die Formel ermöglichen die fehlende dritte Seitenlänge zu berechnen. Wir folgen dazu der Skizze und zerlegen $c=p+q$. Wenden Sie in jedem der kleinen Teildreiecke den Satz des Pythagoras an und leiten Sie damit die allgemeine Formel her:

\[c^2+b^2-2bc\cdot\cos\alpha=a^2\]

Wir wenden zuerst auf das linke und das rechte Dreieck den Satz des Pythagoras an. $$\begin{align*}b^2=p^2+h^2\\ a^2=q^2+h^2\end{align*}$$ Wir eliminieren in der zweiten Gleichung $h^2$, indem wir die erste Gleichung von der zweiten abziehen. $$a^2-b^2=q^2-p^2$$ Nun ist $$q^2=(c-p)^2=c^2-2pc+p^2,$$ da $q=c-p$. Eingesetzt ergibt das nun: $$a^2-b^2=c^2-2pc+p^2-p^2=c^2-2pc$$ Als Letztes sehen wir, dass $p=b\cdot\cos\alpha$. Wir setzen dies ein und erhalten: $$a^2=c^2+b^2-2bc\cdot \cos\alpha.$$

Aufgabe 5: Pythagoras Puzzle

Ziel ist es, geometrisch zu erkennen, dass der Satz des Pythagoras Gültigkeit hat. Schneiden Sie dazu alle geometrischen Formen aus folgender Skizze aus!

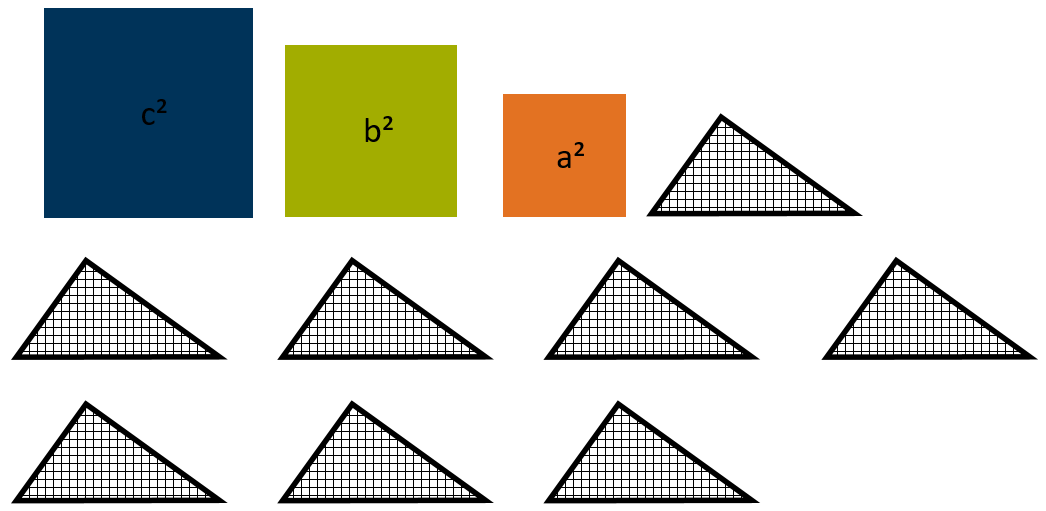
Quadrate und Dreiecke für die Aufgabe

Versuchen Sie nun aus dem großen Quadrat und vier der Dreiecke ein neues Quadrat zu legen. Nehmen Sie dann die verbleibenden vier Dreiecke und die zwei kleinen Quadrate und legen daraus ebenfalls ein Quadrat. Überprüfen Sie, dass die beiden entstandenen Quadrate gleich groß sind; zum Beispiel durch Messen der Seiten. Warum folgt daraus nun, dass $a^2+b^2=c^2$ gilt?

Zurück