Ähnlichkeitsbeziehungen

Um einen Beweis mithilfe von Ähnlichkeitsbeziehungen führen zu können, wird der Flächensatz für ähnliche Figuren benötigt: Die Flächeninhalte ähnlicher Figuren verhalten sich wie die Quadrate entsprechender Strecken. Dies bedeutet beispielsweise, dass wenn eine beliebige ebene Figur um den Faktor 3 in alle Richtungen vergrößert wird, sich ihr Flächeninhalt um den Faktor 9 vergrößert.

Beweis 1

Im bekannten rechtwinkligen Dreieck wird der Höhenfußpunkt $D$ eingezeichnet. Außerdem benennen wir den Fußpunkt des Lotes von $D$ auf $BC$ mit $E$ und den des Lotes von $D$ auf $AC$ mit $F$.

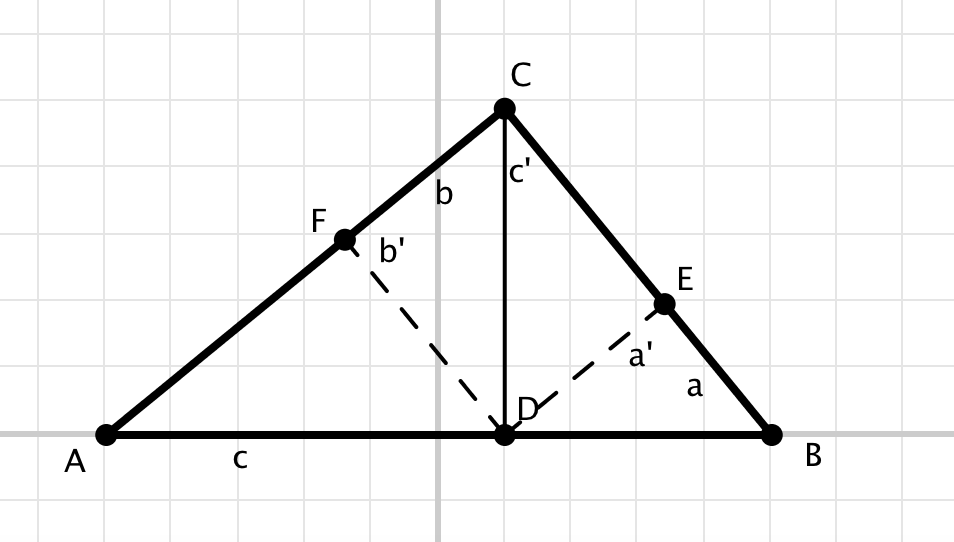
Hinweis: Statische Abbildung.

Die Dreiecke $\triangle CDE$ und $\triangle DCF$ sind kongruent zueinander und ähnlich zum Dreieck $\triangle ABC$.

Somit gilt für $a’=DE$, $b’=DF$ und $c’=DC$ die Beziehung

\[a : a’ \enspace = \enspace b:b’ \enspace = \enspace c:c’.\]

Nun bildet sich das Dreieck $\triangle ABC$ aus den beiden Dreiecken $\triangle ADC$ und $\triangle CDB$, woraus folgt:

\[\frac{cc’}{2}=\frac{aa’}{2}+\frac{bb’}{2}\]

Zusammen mit den Ähnlichkeitsbeziehungen ergibt sich somit \(c^2=a^2+b^2\)

Beweis 2

Wieder nennen wir den Höhenfußpunkt $D$.

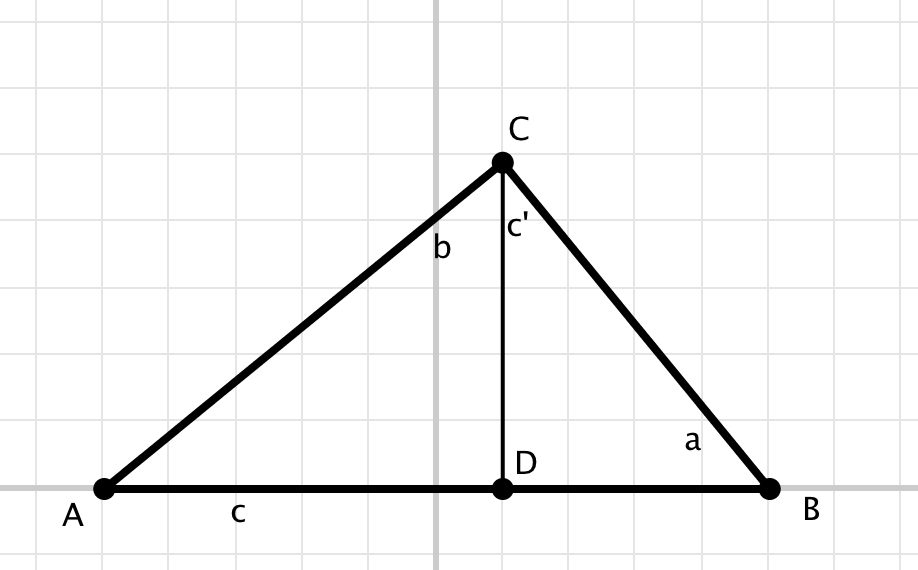
Hinweis: Statische Abbildung.

Aus der Ähnlichkeit der beiden Dreiecke $\triangle ADC$ und $\triangle ABC$ mit $b:c$ folgt: Die Flächeninhalte derselben Dreiecke verhalten sich wie \(b^2:c^2.\)

Analog verfährt man mit den Dreiecken $\triangle BCD$ und $\triangle ABC$ mit $a:c$. Somit verhalten sich die Flächeninhalte wie $a^2:c^2$.

Die beiden Dreiecke $\triangle ACD$ und $\triangle BCD$ ergeben zusammen das Dreieck $\triangle ABC$, woraus folgt:

\[\frac{a^2}{c^2}+\frac{b^2}{c^2}=1\]

Durch Umformung erhält man somit: \(a^2+b^2=c^2\)

Mehr Informationen zum Satz des Pythagoras finden Sie in (Fraedrich, 1995).