Prinzip der Zerlegungsgleichheit

(Fraedrich, 1995)

Zerlegungsbeweise beruhen auf dem Prinzip der Zerlegungsgleichheit. Die Idee ist die folgende:

Zwei ebene Figuren sind genau dann flächeninhaltsgleich, wenn sie zerlegungsgleich sind. Zwei Figuren sind zerlegungsgleich, wenn sie sich in paarweise kongruente Teilfiguren zerlegen lassen.

Das bedeutet also, dass zwei Figuren zerlegungsgleich sind, wenn man sie so zerschneiden kann, dass man aus den entstehenden Teilen, die andere zusammensetzen kann. Die Gesamtfläche bleibt bei einer solchen Operation erhalten.

Zerlegungsbeweis nach Henry Perigal

Auf unser Problem angewandt, bedeutet das, dass der Satz des Pythagoras bewiesen ist, wenn wir die Kathetenquadrate und das Hypotenusenquadrat derart zerlegen können, dass gleiche Teilfiguren entstehen.

Die folgende dynamisch-interaktive Visualisierung demonstriert eine Zerlegung, die auf Henry Perigal zurückgeht und bereits 1830 gefunden wurde. (Fraedrich, 1995)

Was tun: Den weißen Punkt hin und her bewegen. Den Schieberegler rechts von der Figur von unten nach oben bewegen.

Die hier angegebene Zerlegung zeigt, dass die beiden Kathetenquadrate zum Hypotenusenquadrat verformt werden können. Jedoch ist ein wenig Arbeit nötig, daraus einen mathematisch korrekten Beweis zu machen. Da die Art der Zerlegung nicht ganz offensichtlich ist, muss zunächst genau beschrieben werden, wie zu dieser Zerlegung gelangt werden kann und danach erklärt werden, warum die Teile so umsortiert werden können, dass sie das Hypotenusenquadrat ausfüllen. Dies soll im Folgenden geschehen.

Für den Beweis werden die Geraden und Punkte folgendermaßen benannt:

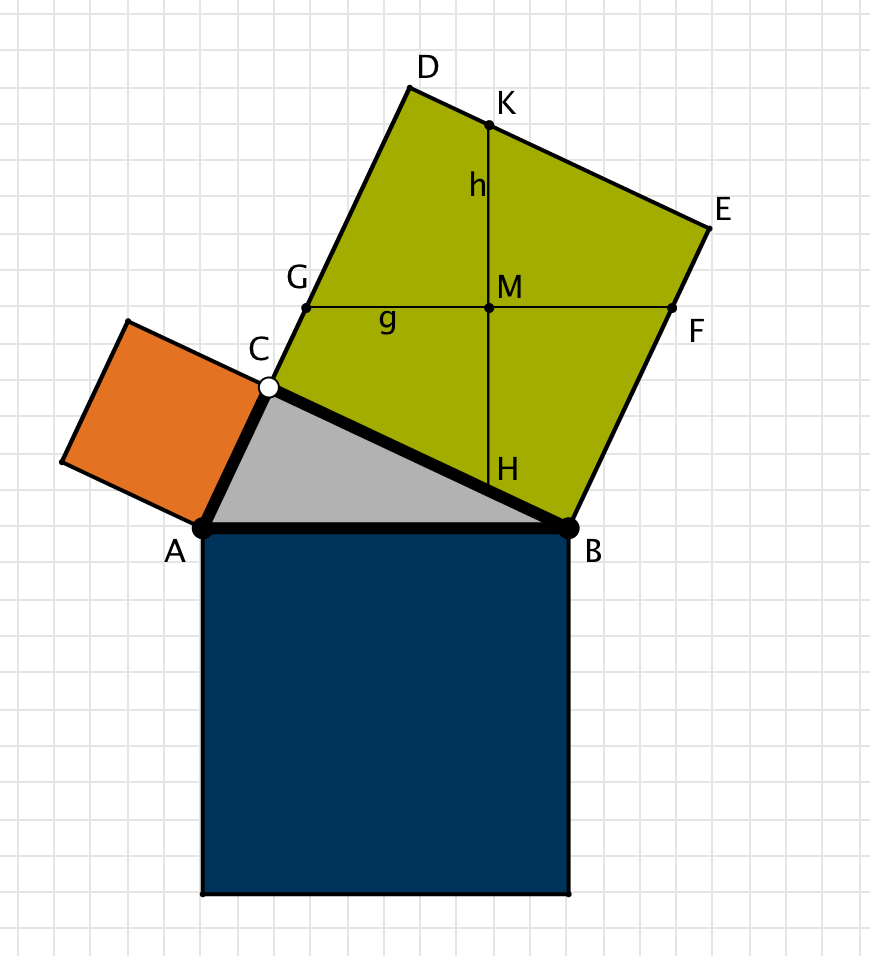Abbildung: “Zum Schaufelradbeweis” in Anlehnung an Faedrich (1995, S. 31)

Seien $a = \vert BC\vert$ und $b = \vert AC\vert$. Der Punkt $M$ sei der Mittelpunkt des größeren Kathetenquadrats. Durch diesen teilen die beiden Geraden $g$ und $h$ das Quadrat, wobei $g$ parallel zur Geraden $AB$ und $h$ senkrecht zur Geraden $AB$ steht. Aufgrund dieser Eigenschaften sind die vier sich so ergebenden Schaufeln kongruent. Wir können, ohne Beschränkung der Allgemeinheit, davon ausgehen, dass das grüne Quadrat das größere ist. Sollte dies nicht der Fall sein, müssen die folgenden Überlegungen mit vertauschten Rollen durchgeführt werden.

Jede Schaufel lässt sich derart verschieben, dass sie in das Hypotenusenquadrat gelegt werden kann, und zwar derart, dass die Schaufeln sich nicht überschneiden und in der Mitte ein Quadrat entsteht, welches zum kleineren Kathetenquadrat kongruent ist.

Wird diese Behauptung belegt, ist der Satz des Pythagoras bewiesen. Wir gehen in mehreren Schritten vor und sammeln zunächst Eigenschaften der Längen und Winkel der vier Schaufeln:

1. Die Länge der Strecke $\vert GF\vert$ ist gleich $c$.

   Dies sieht man daran, dass im Viereck $ABFG$ gegenüberliegende Seiten parallel sind. Das Viereck ist also ein Parallelogramm. In einem Parallelogramm sind gegenüberliegende Seiten gleich lang. Also ist $\vert GF\vert = \vert AB\vert=c$.

2. Es gilt $\vert GM\vert=\vert FM\vert=\vert HM\vert=\vert KM\vert=\frac{c}{2}$.

   Der Punkt $M$ war als Mittelpunkt des grünen Quadrates gewählt. Da die beiden Schnittlinien symmetrisch im Quadrat liegen und wegen $\vert GF\vert =c$, folgt die Behauptung. In anderen Worten: die beiden Seiten einer Schaufel die am Punkt $M$ zusammentreffen haben eine identische Länge von genau $\frac{c}{2}$.

   Wir wollen nun die Längen der beiden anderen Seiten bestimmen.

3. Es gilt $\vert GD\vert=\vert AG\vert=\frac{a+b}{2}$.

   Zunächst beobachten wir, dass einerseits $\vert GD\vert=\vert BF\vert$ gilt, wegen der Symmetrie der Figur. Andererseits gilt $\vert AG\vert=\vert BF\vert$, da $ABFG$ ein Parallelogramm ist. Somit gilt $\vert AG\vert=\vert GD\vert$. Der Punkt $G$ teilt somit die Strecke $\vert AD\vert$ in der Mitte. Wegen $\vert AD\vert=a+b$ gilt $\vert GD\vert=\vert AG\vert=\frac{a+b}{2}$.

4. Es gilt $\vert DK\vert=\frac{a-b}{2}$.

   Aufgrund der Symmetrie der Figur gilt $\vert DK\vert=\vert CG\vert$. Wir haben gerade gezeigt, dass $\vert AG\vert=\frac{a+b}{2}$. Der Punkt $C$ unterteilt die Strecke $\vert A,G\vert$ und es gilt $\vert AC\vert=b$. Also ergibt sich $\vert DK\vert=\vert CG\vert=\vert AG\vert-b=\frac{a+b}{2}-b=\frac{a - b}{2}$.

   Abschließend wollen wir noch eine Aussage über die Winkel bereitstellen.

5. Die Winkel der Schaufel $GMKD$ an den Punkten $G$ und $K$ ergänzen sich zu (180°).

   Dies ergibt sich daraus, dass die Winkelsumme im Viereck stets (360°) ist und wir aufgrund der Konstruktion jeweils einen (90°) Winkel an den Punkten $M$ und $D$ haben.

Nun wollen wir die gesammelten Fakten zu einem Beweis der passgenauen Flächenaufteilung nach der Zerlegung zusammensetzen. Wir gehen in zwei Schritten vor.

Zuerst werden die vier Schaufeln, wie in der Visualisierung ersichtlich, an die Ränder des Hypotenusenquadrats verschoben. Unsere Erkenntnis aus Teilbehauptung 1. sagt, dass die beiden Seiten der Schaufeln, die an einer Kante des Hypotenusenquadrates anliegen, genau die Länge $\frac{c}{2}$ haben, also passgenau die Kanten ausfüllen. Ferner sichert uns Teilbehauptung 5., dass sich die Winkel beim Zusammentreffen in der Kantenmitte genau zu 180° ergänzen. Somit füllen die vier Schaufeln das Hypotenusenquadrat bis auf das kleine Quadrat in der Mitte exakt aus.

Anschließend ermitteln wir die Kantenlänge des kleinen verbleibenden Quadrates in der Mitte. Diese ergibt sich genau aus der Differenz der beiden verbliebenen Seiten der Schaufel. Nach unseren obigen Teilbehauptungen 3. und 4. sind dies aber genau $\frac{a+b}{2}$ und $\frac{b - a}{2}$. Zieht man diese beiden Größen voneinander ab, erhält man: $\frac{a+b}{2} - \frac{a - b}{2} = b$, also genau die Seitenlange des verbleibenden roten Kathetenquadrates.

Hiermit ist die Beweisführung abgeschlossen.