Funktionen
(Greefrath, Oldenburg, Siller, Ulm & Weigand, 2016)
Nach Greefrath et al. (2016, S. 51 ff.) lassen sich folgende Beispiele für die drei Repräsentationsebenen von Funktionen finden.
Reale situative Darstellungen
Phänomene, in denen Größen funktional voneinander abhängen, tragen wesentlich zur Entwicklung des Funktionsbegriffs bei Lernenden sowie zur Ausbildung entsprechender Grundvorstellungen bei. Dazu sollten sie reale Situationen aus der Perspektive der Mathematik betrachten und damit ihren Blick für funktionale Zusammenhänge schulen.
Dies kann mit folgenden Beispielen im Mathematikunterricht erlebbar gemacht werden:
- Die Lernenden gehen mit variierender Geschwindigkeit einen Gang entlang und erkunden dabei die Abhängigkeit des Orts von der Zeit sowie die Abhängigkeit der Geschwindigkeit von Zeit und Ort. Die Zusammenhänge können tabellarisch und grafisch dargestellt werden.
- Aus einem Wasserhahn fließt ein regelmäßiger Strahl in ein Gefäß. Die Höhe des Wasserstandes nimmt mit der Zeit zu. Dieser Zusammenhang wird anhand von Messwerttabellen und Graphen erfasst. Es wird untersucht, wie die funktionale Abhängigkeit zwischen Wasserstand und Zeit von der Form des Gefäßes abhängt.
Überlegen Sie sich ein weiteres Beispiel, einen Zusammenhang erlebbar zu machen.
Grafische Darstellungen
Mit grafischen Darstellungen können funktionale Zusammenhänge visuell fassbar gemacht werden. Im Folgenden werden gängige Darstellungsarten zusammengestellt und jeweils in Bezug auf Vorzüge und Grenzen diskutiert.
Pfeildiagramme
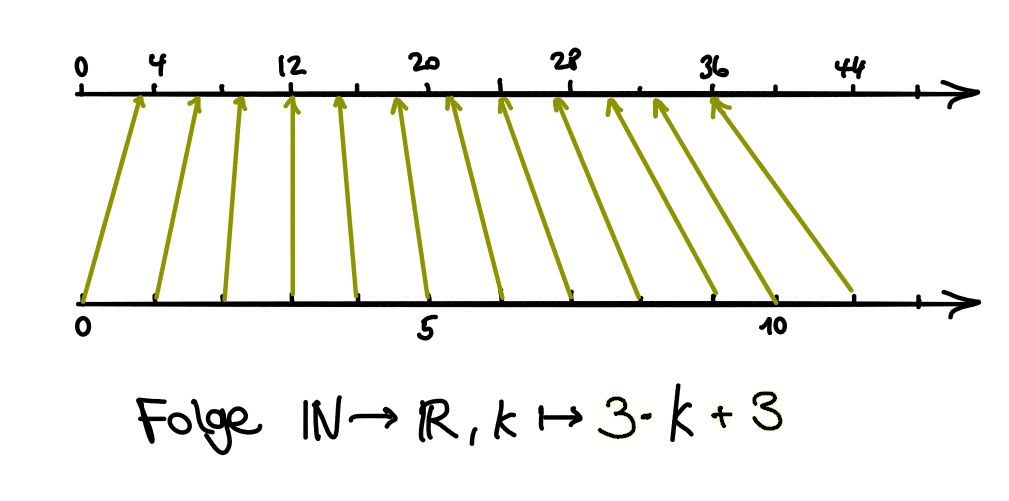
Vorteile:
- Sie stellen die Defintions- und Zielmenge einer Funktion grafisch dar und drücken die Zuordnung von Elementen mithilfe von Pfeilen aus.
- Sie unterstützen die Zuordnungsvorstellung von Funktionen.
- Sie eignen sich zur Illustration der Eigenschaften injektiv/surjektiv/bijektiv und umkehrbar bzw. des Begriffs der Umkehrfunktion.
Grenzen:
- Eine explizite Darstellung der Zuordnung für alle Elemente der Definitionsmenge ist nur sinvoll möglich, wenn die Definitionsmenge nicht allzu viele Elemente enthält.
- Eine Pfeildarstellung verliert an Übersichtlichkeit, wenn sich Pfeile überkreuzen, weil sich etwa monoton steigendes und monoton fallendes Verhalten abwechseln.
Wertetabellen
Eine sehr elementare Darstellung einer Funktion ist die Wertetabelle. Sie stellt die einander zugeordneten Werte unmittelbar neben- oder untereinander dar und drückt damit den Zuordnungs- als auch den Paarmengenaspekt von Funktionen aus.
Grenzen:
Nur wenige Wertepaare können angegeben werden. Die Tabelle kann nur einen kleinen Ausschnitt der Zuordnung darstellen. Die Funktion als Ganzes lässt sich daher nur eingeschränkt erfassen.
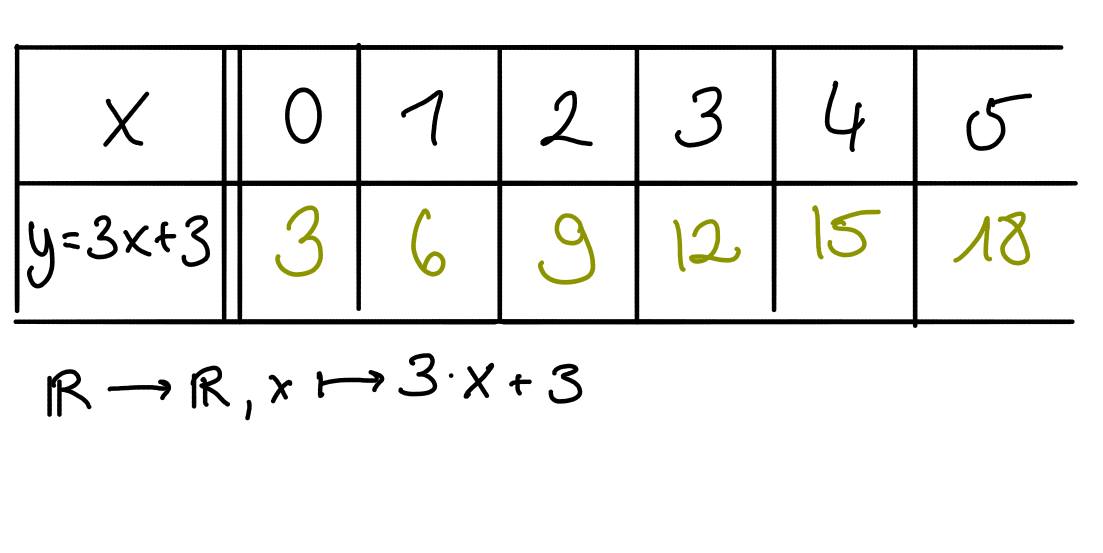
Graphen im Koordinatensystem
Die gebräuchlichste grafische Darstellung von reellen Funktionen ist die Darstellung des Funktionsgraphen in einem kartesischen Koordinatensystem. Die Begriffsbildung kann dabei umittelbar an den Zuordnungsaspekt und den Paarmengenaspekt von Funktionen anknüpfen. Mit Funktionsgraphen können die drei Grundvorstellungen zu Funktionen (Zuordnungsvorstellung, Kovariationsvorstellung, Objektvorstellung; vgl. Greefrath et al. 2016, S. 46 ff.) gefördert werden.
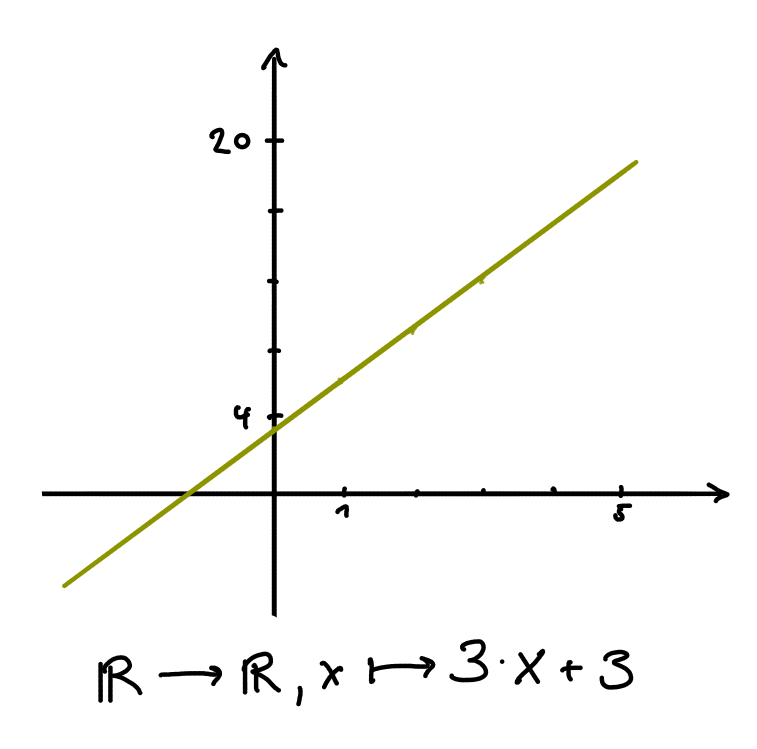
Symbolische Darstellungen
Die meisten Funktionen, die im Mathematikunterricht thematisiert werden, werden in Form einer Zuordnung durch einen algebraischen Term dargestellt. Dies lässt sich durch folgende äquivalente Darstellungen ausdrücken:
- durch einem Funktionsterm: $f(x)=3x+3$
- durch eine Funktionsgleichung: $y=3x+3$
- durch eine Zuordnungsvorschrift: $x\mapsto 3x+3$
Bei Aufgaben sollten Schülerinnen und Schüler stets dazu aufgefordert werden, verschiedene Darstellungsformen funktionaler Zusammenhänge ineinander zu transformieren. Dies dient dazu, ein möglichst umfassendes Verständnis zum Funktionsbegriff aufzubauen. Lernende sollen die Fähigkeit entwickeln, verschiedene Darstellungsformen von funktionalen Zusammenhängen flexibel und problemorientiert zu nutzen und zwischen ihnen zielorientiert zu wechseln.