Bruchzahlen
(Hoch et al., 2018; Padberg & Wartha, 2017, Reinhold, 2018)
Bruchzahlen als Anteil an einem Ganzen
Um Lernenden den Bruchzahlbegriff näher zu bringen, sollte ihnen bei jeder Aufgabe deutlich werden, was das Ganze und was der Anteil ist. Als Einstieg in die Darstellung von Bruchzahlen bietet sich die ikonische Darstellung als Kreise an, da so das Ganze besonders leicht zu sehen ist. Ein klassisches Beispiel für den Anfang ist das Teilen einer Pizza:
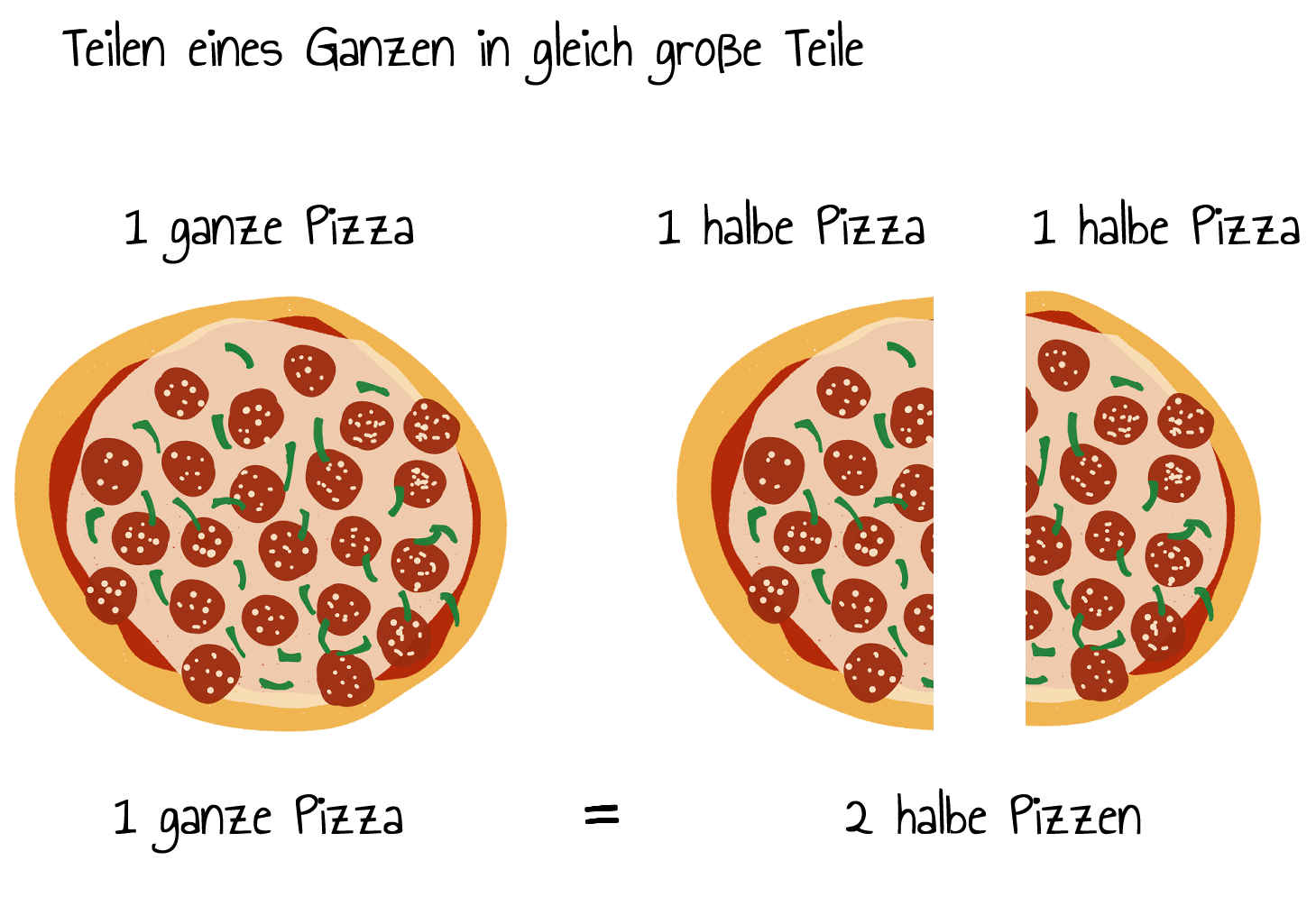
Das Pizza Schneiden als Aufgabenart wurde auch im ALICE-Projekt (Hoch et al., 2018) verwendet, welches an der TUM School of Education durchgeführt wurde und dessen Konzeption, Fragestellungen und Ergebnisse gesammelt in Reinhold (2018) zu finden sind. Dieses wird im Unterrichtsvideo verwendet. Eine Demo-Version können Sie im Folgenden ausprobieren.
Link zur Originalversion
Anleitung: Starten sie die Aufgabe mit einem Klick auf den “Weiter”-Knopf. Anschließend können Sie die Pizzen mit Klicken und Ziehen der Maus zerschneiden bzw. die Pizzastücke verschieben. Die Knöpfe “Zurück” und “Von vorn” machen die letzten beziehungsweise alle Schritte einer Teilaufgabe rückgängig.
Sollen die Lernenden jedoch Teile eines Ganzen selbst herstellen, stellt die komplizierte Umrechnung der Winkel eine Hürde für viele Lernende dar. Hier sollten besser Rechtecke als ikonische Darstellung gewählt werden. Ein weiterer Vorteil der Verwendung von Rechtecken ist, dass diese auch über den enaktiven Zugang verständlich sind. Durch das Falten eines rechteckigen Blattes Papier können besonders leicht Halbe, Viertel, usw. und auch Drittel, Sechstel, usw. dargestellt werden.
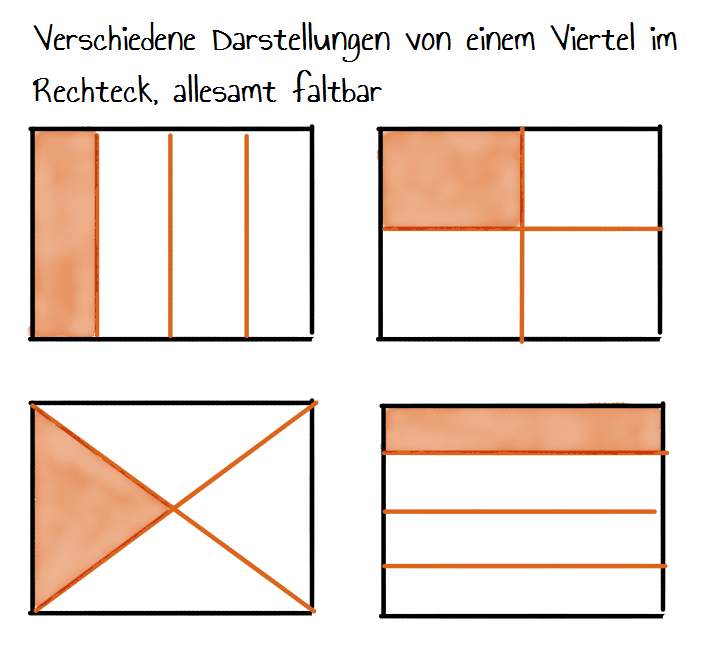
Bruchzahlen als Anteil mehrerer Ganzer
Das gerechte Verteilen von mehreren Ganzen, die in der Gesamtheit das neue Ganze bilden, ist ikonisch ebenso gut darzustellen. Dafür betrachten wir die Aufgabe, bei der drei kleine Blechkuchen an vier Kinder gerecht verteilt werden sollen:
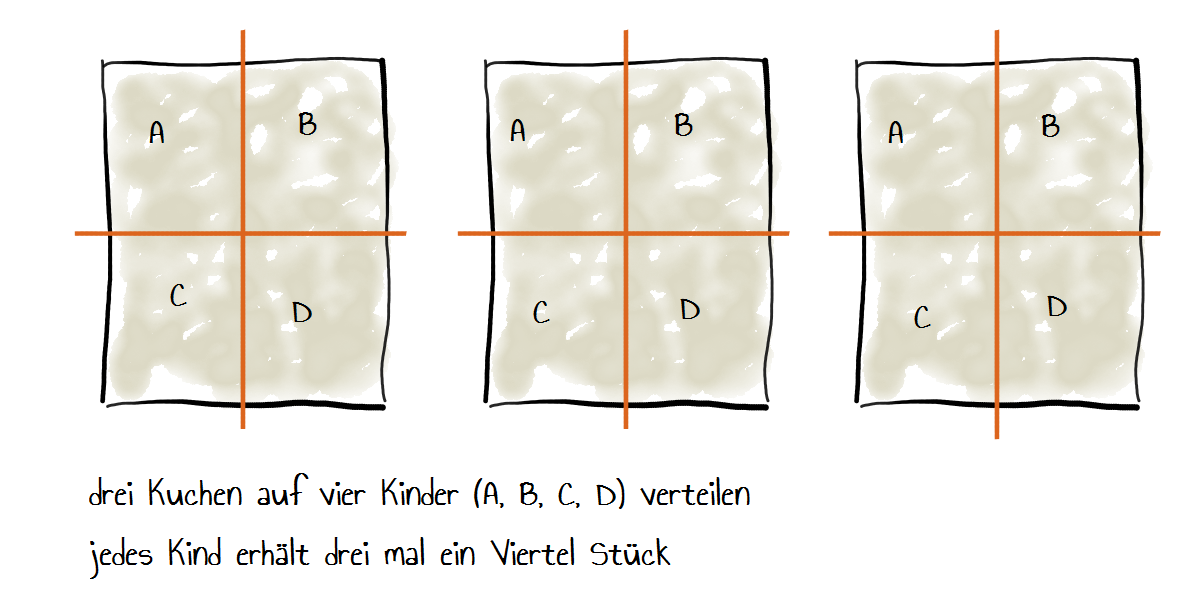
Im Mathematikunterricht sollten beide Aspekte als Grundvorstellung zu Brüchen etabliert und diskutiert werden.
Auch der fachwissenschaftliche Teil dieses Moduls greift das Thema Teil eines Ganzen und mehrerer Ganzer auf.
Rechteck oder Kreis?
Um herauszufinden, ob sich Kreise oder Rechtecke zur Darstellung von Bruchzahlen besser eignen, können folgende Fragen von Padberg & Wartha (2017, S. 32) als Entscheidungskriterien helfen:
- Ist das Ganze klar zu erkennen?
- Kann man die Unterteilung leicht und auf verschiedene Arten durchführen?
- Wie sieht es mit der Einsetzbarkeit im weiteren Verlauf der Bruchrechnung aus (Erweitern/Kürzen, Rechenoperatoren?)
Videobeispiel
In Szene 3: Gruppenarbeit mit Materialien kommen die beiden Lernenden, die sich mit den Bausteinen beschäftigen, immer wieder an die Grenze ihrer zugrunde liegenden Definition des Ganzen. Die Grundplatte funktioniert auf Grund der Unterteilung nicht für alle Brüche. Die Anzahl der Bausteine als Ganzes wirkt nur mit der Unterteilung in zwei Farben. Die Festlegung auf Anteil und Ganzes wird flexibel je nach Situation und Materialangebot verändert.
Beobachten Sie den Umgang mit den anderen Hilfsmitteln. Wie geht die Schülerin mit der Definition von Anteil und Ganzem beim Gummiband um? Wie definieren sich diese beiden Konzepte bei der Arbeit mit den Papierformen?