Fachwissenschaft Informatik: Graphen und Bäume
Wie im Ausblick oben erklärt wurde, können selbst die einfachsten Fragestellungen im Bereich der Graphentheorie zu komplexen und sehr langen Lösungen führen. Dennoch gibt es ein paar Aussagen, deren Beweise kurz und einfach genug sind, um sie im Unterricht verwenden zu können. Ein Paradebeispiel dafür ist die folgende, in der eine Art von vollständiger Induktion verwendet wird, wie sie in Beweisen in der Graphentheorie oft zu finden ist.
Aufgabe 1
Beweisen Sie, dass ein Baum mit $n$ Knoten genau $n - 1$ Kanten besitzt.
Um die Effektivität von Baumsuchen zu illustrieren, eignen sich ganz besonders Folgen aus Ja-Nein-Fragen wie in dem hier verwendeten Unterrichtsvideo. Dort wurden deutsche Politiker verwendet, da diese gerade Thema des Sozialkundeunterrichts waren. Eine Variante, die unabhängig vom Parallelunterricht ist, verwendet Prominente (oder Figuren aus Büchern, Filmen, Spielen usw.) und das Spiel Personenraten (auch “Wer bin ich?” genannt). Eine Schülerin oder ein Schüler denkt sich einen Promi aus und die anderen müssen ausschließlich mithilfe von Ja-Nein-Fragen erraten, wer es ist. Üblicherweise wird hierbei dann die Anzahl der erlaubten Fragen auf zehn beschränkt. Wurde der Promi nach diesen nicht erraten, hat die Schülerin oder der Schüler, die oder der sich den Promi überlegt hat, gewonnen. Anhand dieses Spiel lassen sich nun ein paar einfache Fragen beantworten, um das Prinzip der Baumsuche zu verdeutlichen:
Aufgabe 2
(a) Angenommen, man kann sich auf die schnelle 1000 mögliche Promis überlegen. Welchen Anteil sollte die erste Ja-Nein-Frage idealerweise eliminieren? Welchen Anteil die zweite? Usw.
(b) Wie viele Fragen werden dann in diesem Fall höchstens benötigt, um den Promi zu erraten?
(a) Eine Frage sollte die verbliebene Menge an Kandidaten halbieren. Ist das Verhältnis anders – z.B. 30% bei "Ja" und 70% bei "Nein" – und ist man sich nicht schon sicher, was die Antwort ist, besteht die Chance, dass der größere Anteil übrig bleibt. Bleiben z. B. immer 70% übrig, sind es nach drei Fragen noch 343 Kandidaten. Bei einer Ausschlussquote von 50% sind es dann nur noch 125. Solange man sich also unsicher ist und die Antworten "Ja" und "Nein" gleich wahrscheinlich erscheinen, sollte eine Frage den Kandidatenpool immer halbieren.
(b) Halbiert jede Frage die Anzahl der möglichen Kandidaten, so bleiben nach $n$ Fragen noch $\frac{1000}{2^n}$ Kandidaten übrig. Damit diese Anzahl 1 (oder kleiner) ist, muss $n=10$ sein. Denn $2^9=512< 1000 < 1024 =2^{10}$. Kann man sich also nicht (potenziell) mindestens 1025 verschiedene Promis überlegen, so reichen die 10 Fragen des Spiels aus.
Im Ausblick des Kapitels wurden zwei berühmte Anwendungen der Graphentheorie vorgestellt. Hier nun eine weitere, die sich ebenfalls mit dem Thema der Planarität beschäftigt. Je nachdem, wie ausführlich sie behandelt wird, eignet sie sich für eine Einführungsstunde oder eher für ein W-Seminar.
Aufgabe 3
Gegeben seien drei Häuser und drei Versorgereinrichtungen (z. B. Strom, Wasser und Wärme). Nun sollen Leitungen beziehungsweise Kanäle von allen Versorgern zu allen Häusern gelegt werden. Da diese aber in derselben Tiefe verlegt werden, dürfen sie sich nicht kreuzen. Wie müssen sie liegen? In graphentheoretischer Formulierung: Ist der Graph $K_{3,3}$, der dadurch definiert ist, dass er alle Verbindungen zwischen zwei Mengen von drei Knoten als Kanten enthält, planar?
Zur Veranschaulichung hier die Ausgangssituation und eine falsche Lösung:

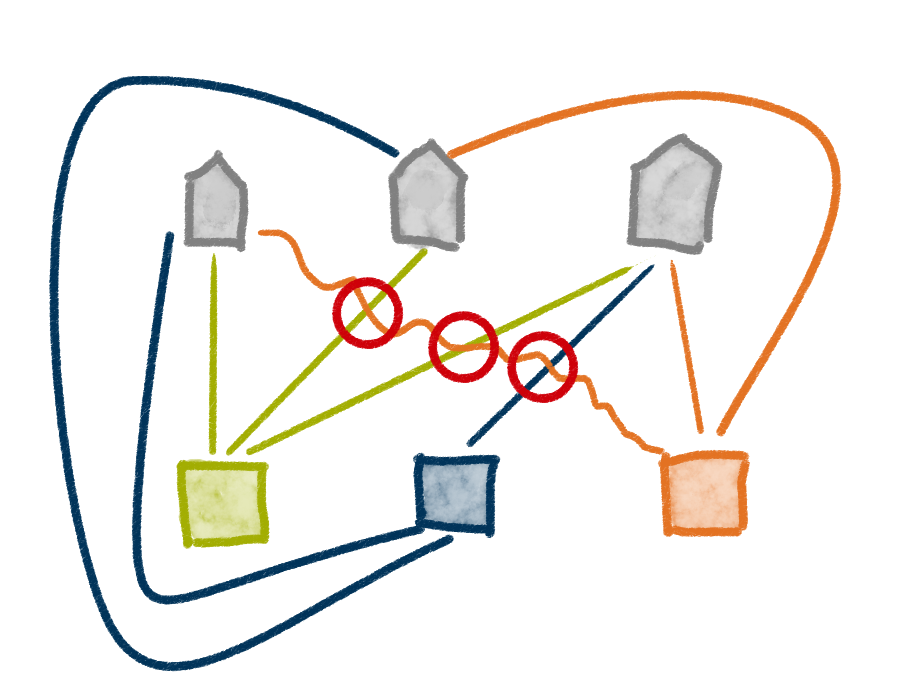
Das ist nicht möglich. Dieser Graph ist einer von zweien, der verhindert, dass ein Graph planar sein kann.
Der Beweis, dass dieser Graph $K_{3,3}$ nicht planar ist, verwendet die Euler'sche Polyederformel. Diese besagt das folgende: Ist ein Graph planar gezeichnet und bezeichnen $n$ die Anzahl seiner Ecken, $m$ die Anzahl seiner Kanten und $f$ die Anzahl seiner Facetten, so gilt immer
$$n - m + f = 2.$$
Hierbei sind die Facetten diejenigen Gebiete der Ebene, die von Kanten eingeschlossen sind. Insbesondere gilt der gesamte Teil der Ebene außerhalb des Graphen als eine Facette.
Mit dieser Formel kann nun für den $K_{3,3}$ bestimmt werden, dass
$$f = 2 - n + m = 2 - 6 + 9 = 5$$
gilt. Allerdings hat jede Facette mindestens vier Kanten: Beginnt ein Kreis, der eine Facette begrenzt, bei z. B. einem der Häuser, so reichen zwei Kanten nicht aus, um zu demselben Haus zurückzugelangen. Und es muss eine gerade Anzahl sein, da die Häuser nicht untereinander verbunden sind. Da jede Kante genau an zwei Facetten sitzt, muss der Graph somit mindestens $\frac{4f}{2}$ Kanten besitzen. Mit $f=5$ von oben sind das also mindestens $10$, was einen Widerspruch darstellt.
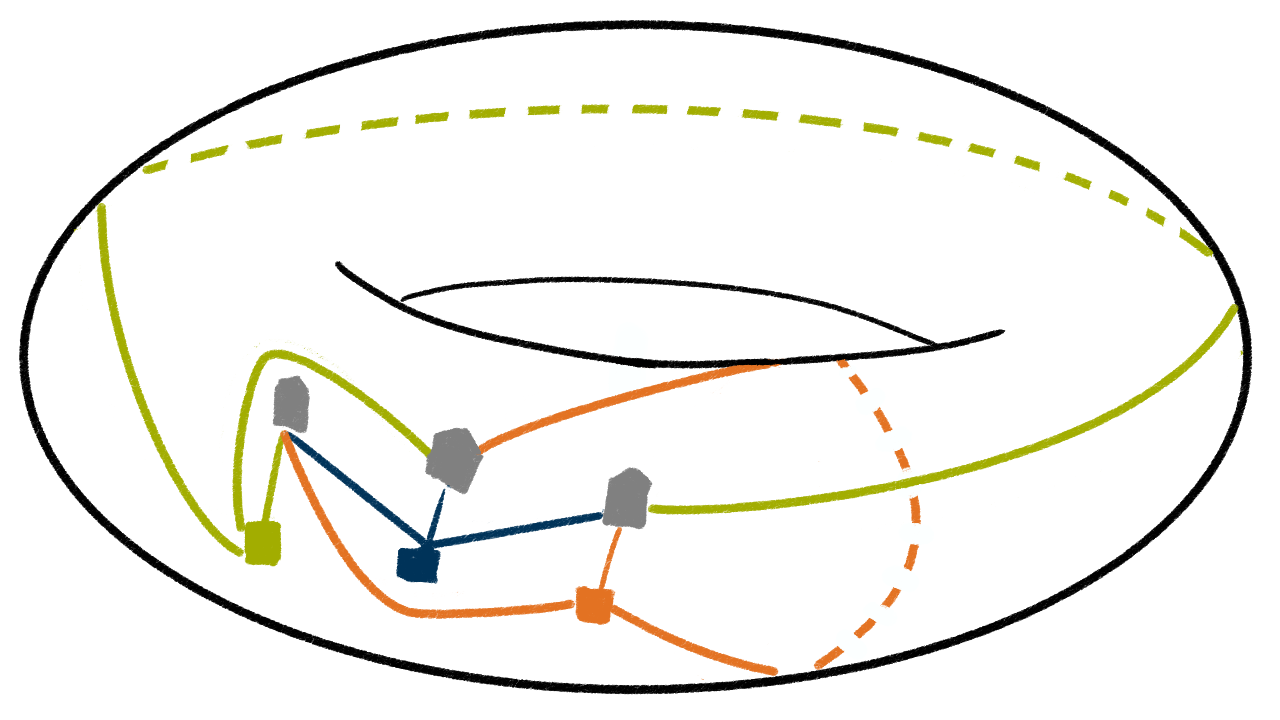
Das Spannende an obigem Problem ist nun, dass es doch lösbar ist, wenn die Häuser und Versorger auf einen Torus gezeichnet werden. Um das umzusetzen beziehungsweise auszuprobieren, können Fahrradschläuche verwendet werden, welche für den Schulunterricht unpraktisch sein können. Allerdings sind Kaffeebecher topologisch äquivalent zu Tori und deswegen können auch diese verwendet werden.
Aufgabe 4
Lösen Sie das Drei-Versorger-Problem aus Aufgabe 3 oben auf einem Torus (beziehungsweise einem Kaffeebecher).
Hier ist die Idee, den Graphen so zu zeichnen, dass nur noch zwei Kanten sich schneiden. Damit diese beiden einander ausweichen können, wird eine Art Brücke benötigt. Das wird auch dadurch klar, dass die Aufgabenstellung in Aufgabe 3 explizit verlangt, dass die Leitungen in derselben Tiefe verlegt sind. Dies muss also integraler Bestandteil der Begründung sein, warum das Rätsel keine Lösung besitzt. Wird es umgangen, indem eine Kante über die andere hinweg gehoben wird, so ist das Problem gelöst.
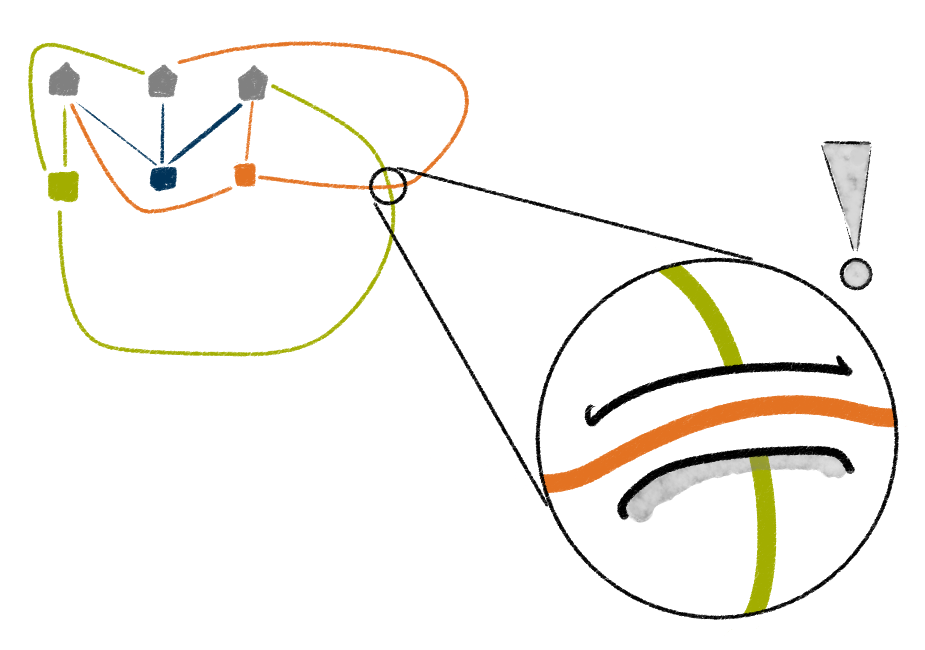
Wird die Brücke, die in die Zeichenfläche eingebaut wurde, aufgebogen, kann dadurch (topologisch) ein Torus gebildet werden. Und zwar so, dass eine der ursprünglich problematischen Kanten horizontal um den "Äquator" des Torus gewickelt wurde (die toroidale Richtung, im Bild unten die grüne Kante) und die zweite Kante vertikal durch das "Loch" des Torus verläuft (die poloidale Richtung, im Bild unten die orange Kante).
Grant Sanderson vom YouTube-Kanal 3blue1brown hat seinen Kollegen dieselbe Aufgabe gestellt. Die Lösungsversuche der Profimathematiker zusammen mit der Begründung zur Nichtlösbarkeit von Aufgabe 3 kann in folgendem Video betrachtet werden.