Weitere trigonometrische Funktionen

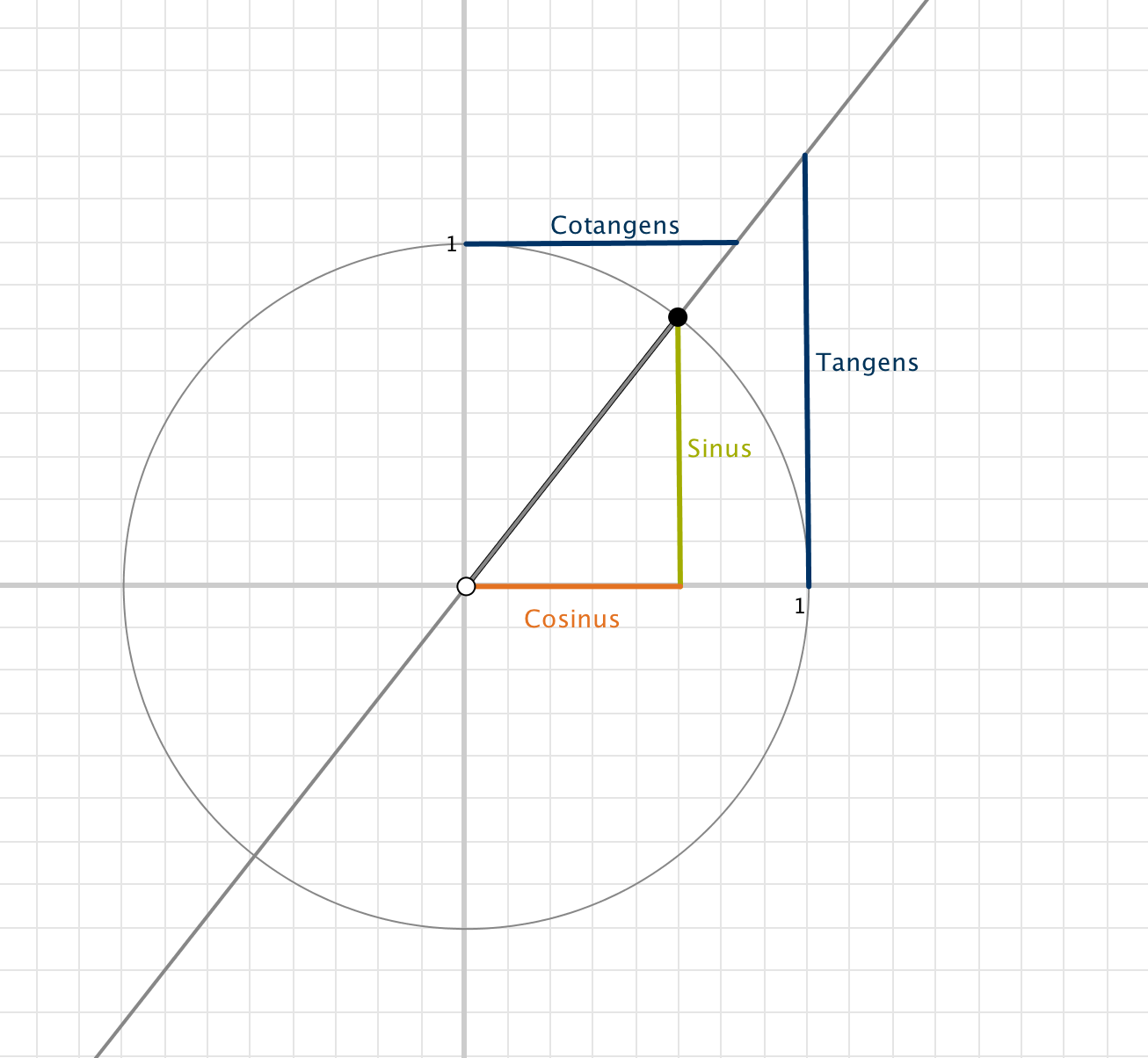
Mit den neu gewonnen Funktionen $\sin(x)$ und $\cos(x)$, kann nun eine weitere große Vielzahl an trigonometrischen Funktionen definiert werden. Die folgende Liste gibt eine kompakte Übersicht über die weiteren gängigen Funktionen:

• Tangens: $\displaystyle{\tan(x)=\frac{\sin(x)}{\cos(x)}}$
• Kotangens: $\displaystyle{\cot(x)=\frac{\cos(x)}{\sin(x)}}$
• Sekans: $\displaystyle{\sec(x)=\frac{1}{\cos(x)}}$
• Kosekans: $\displaystyle{\csc(x)=\frac{1}{\sin(x)}}$

Vorsicht ist geboten, falls man die Begriffe Sinus Hyperbolicus oder Cosinus Hyperbolicus schon einmal gehört hat. Diese Funktionen stammen nicht aus dem Universum der trigonometrischen Funktionen, sondern stellen die Paritätszerlegung der $e$-Funktion dar.