Woher stammt der Satz des Pythagoras?

(Fraedrich, 1995)

Es ist nicht festzustellen, wann und wo der Satz des Pythagoras zum ersten Mal Anwendung fand. Jedoch gibt es viele Vermutungen (Fraedrich, 1995). Eine davon ist die Geschichte der Seilspanner, welche hier exemplarisch angesprochen wird.

Bereits lange vor der Geburt von Pythagoras (um 570 v. Chr. auf Samos) wurde das Wissen über rechtwinklige Dreiecke von den Ägyptern genutzt. In der Jungsteinzeit (um 4500 - 2000 v. Chr.) entstanden megalithische Bauten in denen pythagoreische Dreiecke zu finden sind. Sogenannte Seilspanner hatten zur Aufgabe, rechtwinklige Dreiecke mithilfe eines Seils zu spannen. Hierzu nutzten sie ein Seil, welches an beiden Enden zusammen geknotet war und teilten dieses in 12 identische Stücke mithilfe von Knoten auf. Sie spannten das Seil nun auf, indem sie es am ersten, vierten und achten Knoten festhielten. Am vierten Knoten ergab sich durch diese Anordnung ein rechter Winkel.

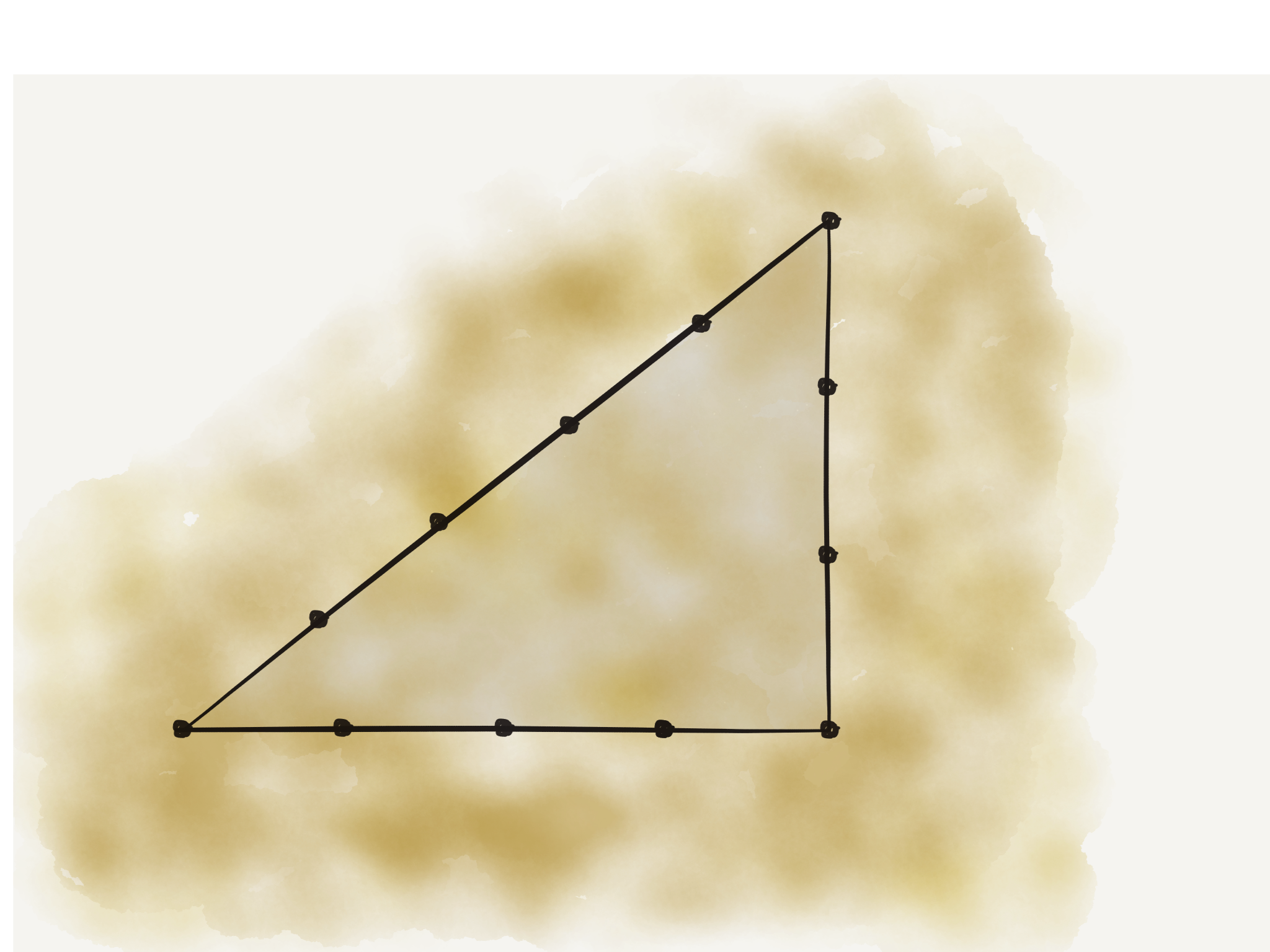
Dieses pythagoreische Dreieck $(3,4,5)$ mit der Gleichung $3^2+4^2=5^2$ ist nur eines von vielen pythagoreischen Tripeln – d.h. drei ganze Zahlen, welche den Satz des Pythagoras erfüllen.

Bei der berühmten Stufenpyramide des Djoser wurden mehrere pythagoreische Tripel nachgewiesen, ob dies vom Erbauer nun wirklich so gewollt war kann nur vermutet werden.

Die Besonderheit bei dem Seilspanntrick: Die Seilspanner gehen von der Gleichung aus und folgern daraus, dass ein rechter Winkel entsteht. Sie gingen damit von der Umkehrung des Satzes aus, welcher daher älter sein dürfte als der Satz selbst.

Die Theorie hinter den pythagoreischen Tripeln wird im Abschnitt Spezialisierungen angesprochen.