Laufzeit
Nachdem die Schülerinnen und Schüler in Szene 6: Anwendungen von Binärbäumen sich das Wörterbuch als Binärbaum selbst erarbeitet haben, bespricht der Lehrer mit ihnen, wie viele Überprüfungen benötigt werden, um ein Element zu finden. Diese Diskussion ist an dieser Stelle sehr wichtig, um den Schülerinnen und Schülern zu verdeutlichen, worin der große Vorteil von Binärbäumen als Datenstrukturen besteht. Um diesen Punkt zu veranschaulichen, kann auch in einem echten Wörterbuch mit tausenden von Einträgen gesucht werden. Jeder Eintrag der hinreichend weit hinten steht, wird über die Baumsuche sehr viel schneller gefunden werden, als über eine Suche, die am Anfang des Wörterbuchs startet und einfach nur der Reihe nach hinten verläuft.
Wie groß der Unterschied zwischen Baumsuche und einfacher Listensuche ist, soll hier konkret bestimmt werden.
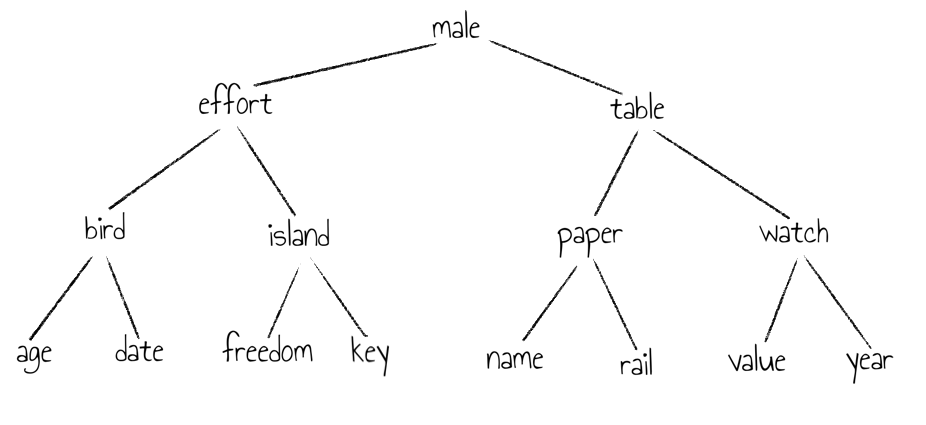
In obigem Beispiel ist ein Binärbaum mit $4$ Ebenen gegeben und es haben insgesamt
\[1+2+4+8 = 15 = 2^4 - 1\]
Wörter Platz. Dieser Zusammenhang lässt sich verallgemeinern:
Satz: Ein Binärbaum mit $n$ Ebenen, für $n\in\mathbb{N}^+$, hat $\sum_{i=1}^{n-1} 2^i = 2^n - 1$ Knoten.
Beweis: Das lässt sich sehr einfach mittels vollständiger Induktion beweisen. Für $n=1$ hat der Baum nur eine Ebene und in dieser befindet sich nur die Wurzel. Es sind also $2^1 - 1=1$ Knoten.
Angenommen, die Aussage, und insbesondere die Identität $\sum_{i=1}^{n-1}2^i = 2^n - 1$, für $n$ stimmt. Hat ein Baum $n+1$ Ebenen, so befinden sich in der letzten Ebene insgesamt $2^n$ Knoten. Insgesamt sind es damit dann
\[\sum_{i=1}^n 2^i = \sum_{i=1}^{n-1} 2^i + 2^n = (2^n - 1) + 2^n = 2^{n+1} - 1\]
Knoten.
Wenn also eine geordnete Liste mit $N$ Einträgen als Binärbaum gespeichert werden soll, so muss dieser $\lceil \log_2(N + 1)\rceil$ Ebenen haben. Alle Knoten, die dabei zu viel sind, werden leer gelassen. Zum Beispiel ist
\[2^4 - 1\enspace <\enspace 20\enspace <\enspace 2^5 - 1.\]
Also werden 5 Ebenen benötigt, um 20 Elemente speichern zu können.
Das bedeutet insbesondere, dass eine Liste immer mit höchstens $\lceil \log_2(N + 1)\rceil$ Abfragen durchsucht werden kann. Ist zum Beispiel eine Liste mit 1000 Einträgen gegeben und der 800ste gesucht, so müssen bei einer normalen Liste insgesamt 800 Abfragen durchgeführt werden. Da $2^9 - 1 < 1000 < 2^{10} - 1$, kann diese Liste als Binärbaum gespeichert werden, in dem 10 Abfragen reichen, um dieses Element zu finden. Die einzigen Elemente, die in einer Liste schneller gefunden werden können, als in einem Baum, sind diejenigen, die relativ weit vorne stehen. Ein Vergleich zwischen Listensuche und Baumsuche für verschiedene Elementzahlen kann in der nachfolgenden dynamisch-interaktiven Visualisierung betrachtet werden.
Die blauen Rechtecke in der Mitte stellen die Einträge einer geordneten Datenmenge dar – wie etwa einem Wörterbuch. Für den Fall, dass es 15 Stück sind, sind es genau die Wörter aus obigem Beispiel. Die Zahlen oben und unten geben an, wie lange es dauert, um einen Eintrag zu finden. Dabei stellen die Zahlen oben die Listensuche dar, bei der einfach von links nach rechts durch die Datenmenge gelaufen wird, bis das entsprechende Element gefunden wurde. Die unteren Zahlen beschreiben die Binärbaumsuche, wie sie hier eingeführt wurde.
Anleitung: Am Schieberegler rechts die Anzahl der Elemente der Datenmenge verändern. Über die blauen Datenrechtecke fahren, um die zugehörigen Suchzeiten hervorzuheben.
Weiterführende Informationen zu Bäumen als Datenstrukturen finden Sie in (Dietzfelbinger, Mehlhorn, & Sanders, 2014).