Gewurzelte Bäume
Im Folgenden sollen Bäume als spezielle Datenstruktur betrachtet werden. Insbesondere, als eine, welche die bekannten Listen verallgemeinert. Diese Bäume sollen gerichtet sein und alle Blätter sollen von einem bestimmten Startknoten aus erreichbar sein. Dieser spezielle Knoten wird Wurzel genannt. Das bedeutet, dass ausgehend von ein und demselben allgemeinen Baum unterschiedliche gerichtete Bäume entstehen können, je nachdem welcher Knoten als Wurzel gewählt wird. In so einem Baum wird bei einer Verbindung $A\to B$ der Knoten $B$ das Kind von $A$ genannt und umgekehrt $A$ der Elternknoten von $B$.
In der Skizze unten ist ein allgemeiner Baum zu sehen, der zu einem gewurzeltem Baum gemacht wird. Wird der blaue Knoten als Wurzel gewählt, entsteht der gerichtete Graph unten links; wird der orange als Wurzel gewählt, so entsteht der gerichtete Graph unten rechts.
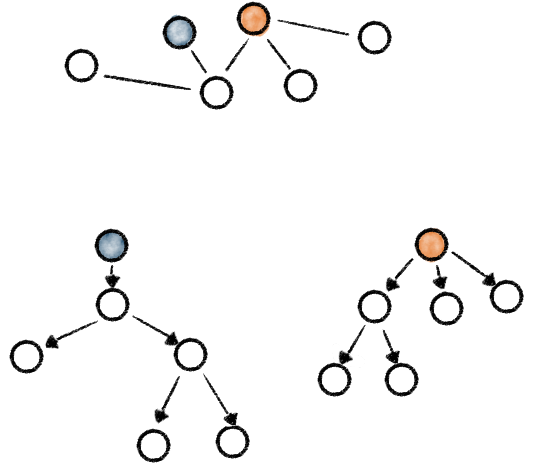
Wenn so ein gewurzelter, gerichteter Baum gezeichnet wird, ist die Wurzel immer ganz oben und die Kinder sind immer unterhalb der jeweiligen Elternknoten. Und da zwangsläufig alle gerichtete Kanten immer nach unten zeigen, wird oft darauf verzichtet, die Pfeilspitzen zu zeichnen.
Ab jetzt werden nur noch solche gerichteten Bäume mit Wurzel betrachtet und das Ziel ist, zu überlegen, was mit ihnen (in der Informatik) modelliert werden kann.
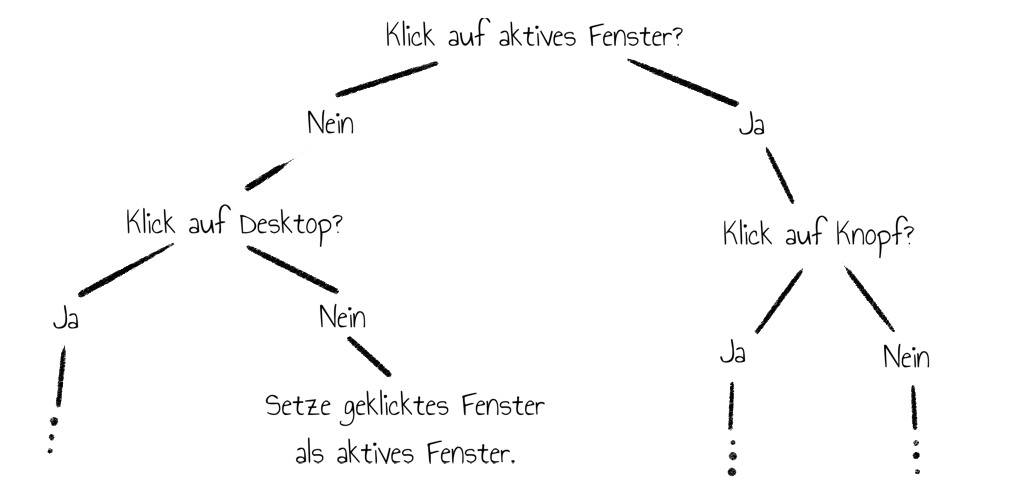
Die Grundidee hier ist, dass solche Bäume immer eine Abfolge von Entscheidungen darstellen. Diese können in größeren Computerprogrammen komplexe Abfolgen modellieren. Wenn z.B. mit dem Cursor auf einem Bildschirm auf eine beliebige Stelle geklickt wird, entscheidet das Betriebssystem anhand diverser Abfragen, welche Operation ausgeführt werden soll.
Ein großer Vorteil sich gewurzelten Bäumen als Flussdiagramms eines Entscheidungsprozesses zu nähern, besteht darin, sehr leicht andere Themengebiete verwenden zu können, die den Schülerinnen und Schülern vertraut sind. So zeigt Szene 3: Partnerarbeit dieselbe Idee anhand der deutschen Bundesminister, da diese gerade Thema des Sozialkundeunterrichts sind.
Weiterführende Informationen zu Bäumen als Datenstrukturen finden Sie in (Dietzfelbinger, Mehlhorn, & Sanders, 2014).