Das Sieb des Eratosthenes

Primzahlen spielen eine wichtige Rolle in der Mathematik, besonders in der Zahlentheorie. Zum Beispiel besagt der Fundamentalsatz der Zahlentheorie das Folgende: Jede positive, ganze Zahl $n$ besitzt eine Darstellung als Produkt von Primzahlen $n=p_1\cdot p_2\cdot\cdots\cdot p_k$ mit $k>0$, welche bis auf die Reihenfolge der Faktoren eindeutig ist.

Ein anderer zentraler Satz über Primzahlen stammt von Euklid und besagt, dass es unendlich viele von ihnen gibt. Doch wie können diese Primzahlen bestimmt werden? Ein mögliches Verfahren ist das Sieb des Eratosthenes. Damit können sehr einfach alle Primzahlen bestimmt werden. Allerdings ist es in der Praxis üblich, die Suche auf den Bereich $1$ bis $n$ zu beschränken, da es, wie eben gesagt, unendlich viele Primzahlen gibt. Angenommen, es gibt so eine Obergrenze, so sieht der Algorithmus wie folgt aus:

Notiere alle Zahlen von 1 bis n.
Streiche die 1 weg.
Solange es noch unmarkierte Zahlen gibt, tue:
|     Umkreise die kleinste unmarkierte Zahl.
|     Streiche alle echten Vielfachen dieser Zahl.
Alle am Ende umkreisten Zahlen sind Primzahlen.

Werden z.B. die Zahlen von $1$ bis $12$ betrachtet, sehen die Zwischenergebnisse dieses Algorithmus wie folgt aus:

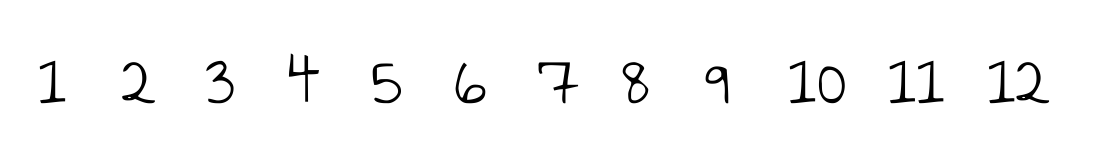
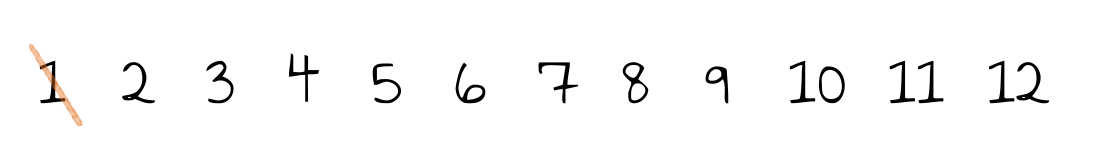
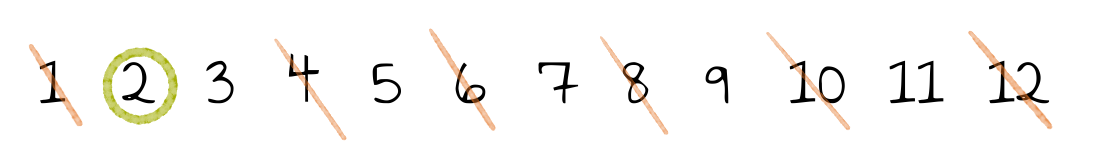
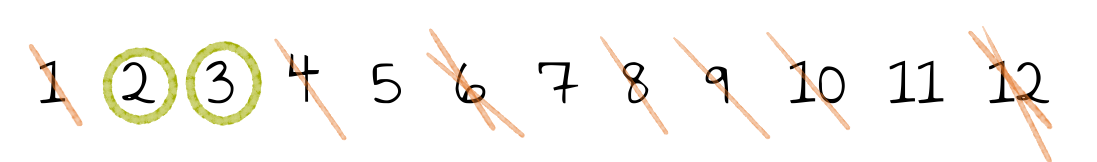
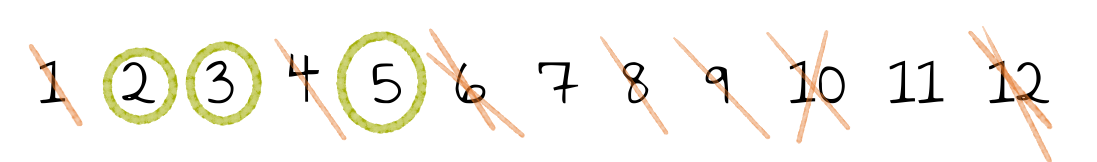
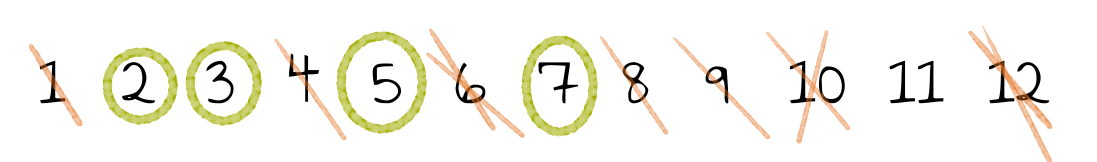
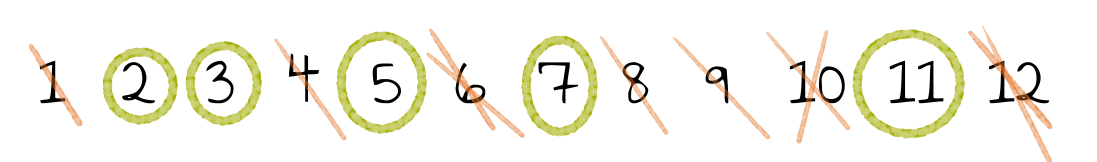
Oft ist es aufwendig zu zeigen, dass Algorithmen auch tatsächlich das liefern, was sie sollen. Hier ist es allerdings sehr einfach, was das Sieb des Eratosthenes zu einem guten Beispiel für den Schulunterricht macht. Die Begründung für die Korrektheit dieses Verfahrens ist die Folgende: Die kleinste unmarkierte Zahl ist kein Vielfaches einer vorhergehenden Primzahl. Damit muss sie selbst eine Primzahl sein.

Obwohl dieser Algorithmus an sich sehr einfach ist, ist er recht langsam. Soll – z.B. für eine Anwendung in der Kryptographie – eine Primzahl größer als $10\,000\,000$ bestimmt werden, muss hier trotzdem bei $1$ begonnen und alle Primzahl kleiner als $10\,000\,000$ bestimmt werden.

All diese Vor- und Nachteile können in nachfolgender dynamisch-interaktiver Visualisierung beobachtet werden. Allerdings sei hier darauf hingewiesen, dass Schülerinnen und Schüler ein sehr viel besseres Verständnis für diesen Algorithmus entwickeln, wenn sie ihn selbst mit Stift und Papier durchführen. Dabei bieten sich die Zahlen von 1 bis 100 an, damit es nicht zu lange dauert, die Schülerinnen und Schüler aber die Systematik verinnerlichen können. Die nachfolgende Visualisierung stellt hingegen eine Anschauungshilfe dar, wenn der Algorithmus an sich bereits grob verstanden wurde.

Anleitung: Am Schieberegler rechts die zu durchsuchende Menge an Zahlen verändern. Auf den grünen Los!-Knopf drücken, um den Algorithmus zu starten. Mit den “Pause”- und “Weiter”-Knöpfen kann die Suche angehalten werden und der Schieberegler daneben erlaubt das Verändern der Geschwindigkeit.