Einführung und Motivation

Die Suche nach bestimmten Informationen spielt in unserem Leben eine wichtige Rolle. Dabei erleichtert es den Alltag erheblich, wenn gesuchten Informationen schnell gefunden werden können.

Möchte jemand beispielsweise ein bestimmtes Buch aus einer Bibliothek ausleihen, so muss hierfür bekannt sein, wo genau es steht. Und aus Zeitgründen ist es sinnvoll, wenn das systematisch herausgefunden werden kann. Nach welchem System die Bücher sortiert werden, ist von Bibliothek zu Bibliothek unterschiedlich. So kann beispielsweise eine alphabetische, chronologische oder thematische Sortierung eine sinnvolle Einteilung darstellen. Und viele Bibliotheken verwenden einen alphanumerischen Code, um die Bücher basierend auf dieser Kategorisierung in eine feste Reihenfolge zu bringen.

Angenommen der Leiter einer Bibliothek mit mehreren tausend Büchern möchte diese alphabetisch anordnen. Was ist das beste Vorgehen, damit dieser Prozess möglich effizient vonstattengeht?

An diesem Beispielszenario sollen die wichtigsten Sortieralgorithmen vorgestellt werden. In der Informatik werden mithilfe dieser Algorithmen Datenmengen sortiert. Jeder einzelne Algorithmus hat seine Vor- und Nachteile und ist somit für bestimme Situationen besser oder schlechter geeignet.

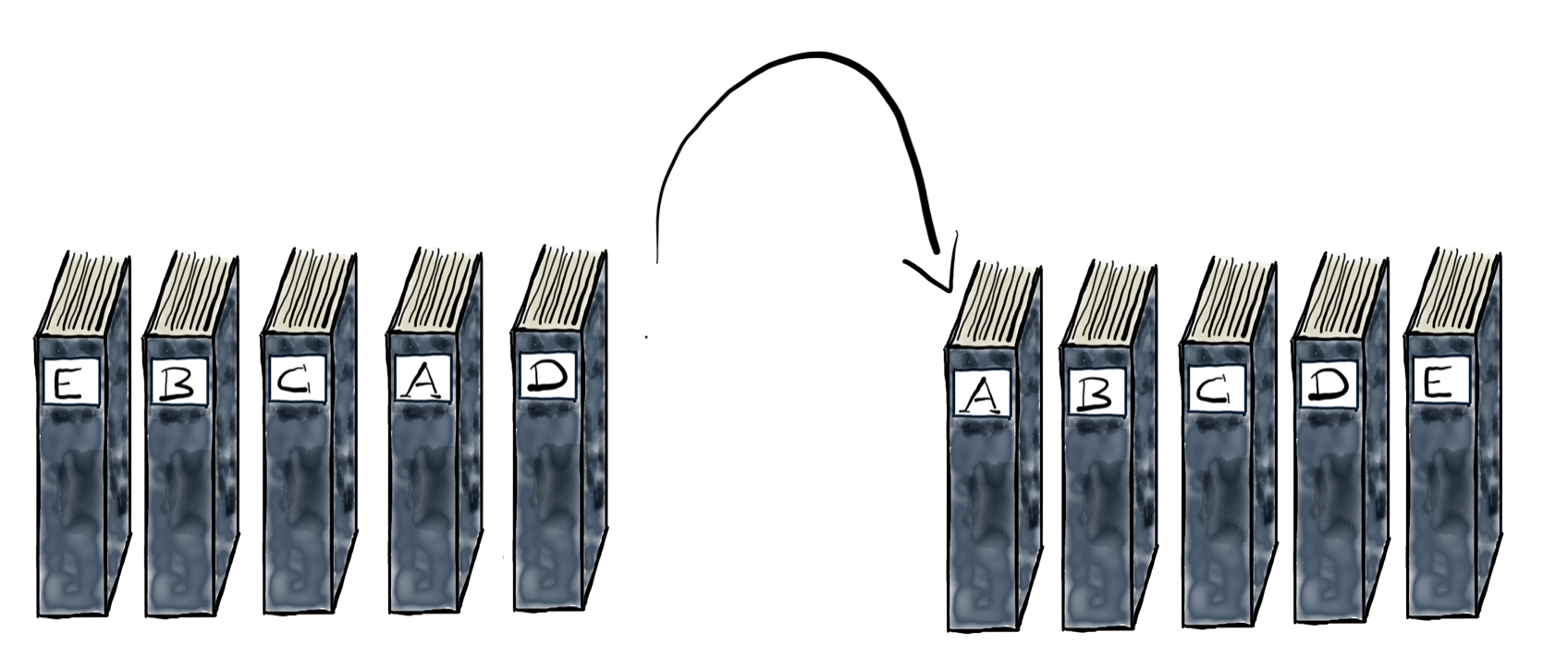
Der Grundaufbau dieser Verfahren ist dabei immer gleich beziehungsweise sehr ähnlich: Gegeben ist eine Liste (ein Array) von Objekten, die in zufälliger Reihenfolge vorliegen und dementsprechend indiziert sind. Ist also z.B. ein Stapel Bücher in der Liste sammlung gespeichert, so ist das Element sammlung[i] einfach das i-te Buch im Stapel.

Nun hat jedes Element der Liste noch einen Schlüssel (englisch: key), der es erlaubt, danach zu sortieren. Dieser Schlüssel muss also ein Datentyp sein, für den die Vergleichsoperatoren <,=,> implementiert sind. Dementsprechend sind es meist ganze Zahlen (wie z.B. bei Matrikelnummern von Studierenden) oder Strings (die, wie im Beispiel hier, den Titel des Buches angeben). Für die nachfolgenden Algorithmen ist es hierbei irrelevant, wie diese Schlüssel verglichen werden können, sondern nur, dass es möglich ist. Dann geben diese Algorithmen eine Umsortierung/Permutation der Liste sammlung aus, so dass für alle Indizes i gilt, dass sammlung[i].key <= sammlung[i+1].key. Sprich, am Ende soll der Bücherstapel so sortiert sein, dass die kleinen Titel (vorne im Alphabet) unten und die großen Titel (hinten im Alphabet) oben sind. (Es ist hierbei erlaubt, dass zwei aufeinanderfolgende Elemente bezüglich der Schlüssel gleich sind. In einer echten Bibliothek tragen viele Bücher denselben Titel.)

Mehr Informationen zu Algorithmen finden Sie unter (Dieker & Güting, 2018).