Arten

Algorithmen können oft in Kategorien einsortiert werden, die ihre allgemeine Funktionsweise beschreiben. Hier sei nun eine kurze Übersicht über einige wichtige dieser Kategorien gegeben. Allerdings passt nicht jeder Algorithmus sauber in eine dieser Schubladen, insbesondere wenn sie einfach und kurz sind.

Rekursive Algorithmen

Rekursionen bestehen im Wesentlichen aus Vorschriften, die sich selbst aufrufen. Es entsteht ein Effekt, der auch aus dem Alltag bekannt ist. Zum Beispiel bei einer Bild-Im-Bild-Funktion an einem Bildschirm oder bei sich gegenüberstehenden Spiegeln…

Dieses Beispiel unterscheidet sich in zwei wesentlichen Punkten von rekursiven Algorithmen in Computerprogrammen:

1. Ein rekursiver Algorithmus braucht eine Abbruchbedingung, um die Terminierung zu garantieren. Bei gegenüberliegenden Spiegeln ist das nicht gegeben und es sind, theoretisch, unendlich viele Spiegelbilder zu sehen. Aber damit ein Computerprogramm in endlicher Zeit seine Arbeit erledigt oder nicht die Grenzen des endlichen Speichers überschreitet, brauchen sich selbst aufrufende Anweisungen in Algorithmen immer ein Ende.
2. Rekursive Algorithmen rufen sich selbst meist mit veränderten Parametern auf. Im Gegensatz zu dem Spiegelbeispiel oben ist es in einem Computerprogramm selten der Fall, dass ein und derselbe Befehl immer wieder auf genau dieselbe Art und Weise ausgeführt werden soll, sondern immer mit leichten Änderungen.

Als Beispiel hier die Berechnung von $n!$, die bereits im Abschnitt über Pseudocodes zu sehen war. Dort wurde sie als Produkt

\[1\cdot 2 \cdot \cdots \cdot n\]

eingeführt. Die Implementierung so eines Produkt ist relativ kompliziert, wie der dort zu sehende C/C++-Code zeigt. Allerdings kann die Fakultät geschrieben werden als

\[n!=n\cdot(n-1)!\]

Das erlaubt die Formulierung eines Algorithmus in der folgenden deutlich kürzeren Form:

fakultaet(n) = {
    Ist n = 0?
        Falls ja, gib das Ergebnis 1 aus.
        Falls nein, gib das Ergebnis n * fakultaet(n - 1) aus.
}

Zum Berechnen von z. B. $6!$ mittels obigen Codes, versucht der Computer $6\cdot 5!$ zu bestimmt. Und dafür muss er mit denselben Anweisungen, aber einem anderen Startwert $5!$ berechnen. Das wird so lange fortgesetzt, bis $0!$ zu berechnen ist, welches fest als $1$ vorgegeben ist. Somit rechnet der Computer mit obiger Funktion das Folgende:

\[6! = 6\cdot 5!\]

\[6! = 6\cdot (5\cdot 4!)\]

\[6! = 6\cdot (5\cdot (4\cdot 3!))\]

\[6! = 6\cdot (5\cdot (4\cdot (3\cdot 2!)))\]

\[6! = 6\cdot (5\cdot (4\cdot (3\cdot (2\cdot 1!))))\]

\[6! = 6\cdot (5\cdot (4\cdot (3\cdot (2\cdot (1 \cdot 0!)))))\]

\[6! = 6\cdot (5\cdot (4\cdot (3\cdot (2\cdot (1 \cdot 1)))))\]

\[6! = 6\cdot (5\cdot (4\cdot (3\cdot (2\cdot 1))))\]

\[6! = 6\cdot (5\cdot (4\cdot (3\cdot 2)))\]

\[6! = 6\cdot (5\cdot (4\cdot 6))\]

\[6! = 6\cdot (5\cdot 24)\]

\[6! = 6\cdot 120\]

\[6! = 720\]

Der gesamte Rechenaufwand ist hierbei gleichgeblieben im Vergleich zur naiven Implementierung im vorhergehenden Abschnitt.

Ein anderes Beispiel, was eher spielerischen Charakter hat und deshalb gut als Rätsel in der Schule verwendet werden kann, sind die Türme von Hanoi. Die Aufgabe lautet wie folgt: Ein Turm besteht aus $n$ aufeinandergestapelten, immer kleiner werdenden Plättchen (auf Platte $A$). Der Turm soll nun an einer neuen Stelle (auf Platte $C$) genauso wieder aufgebaut werden, wobei es zwei Regeln gibt.

1. Es darf immer nur das oberste Plättchen eines Stapels bewegt werden.
2. Es dürfen nur kleinere auf größere Plättchen gelegt werden.

Zusätzlich gibt es noch einen Hilfsstapel (auf Platte $B$), welcher nach den gleichen Regeln gebaut werden kann. Wie kann dieses Problem durch einen rekursiven Algorithmus gelöst werden?

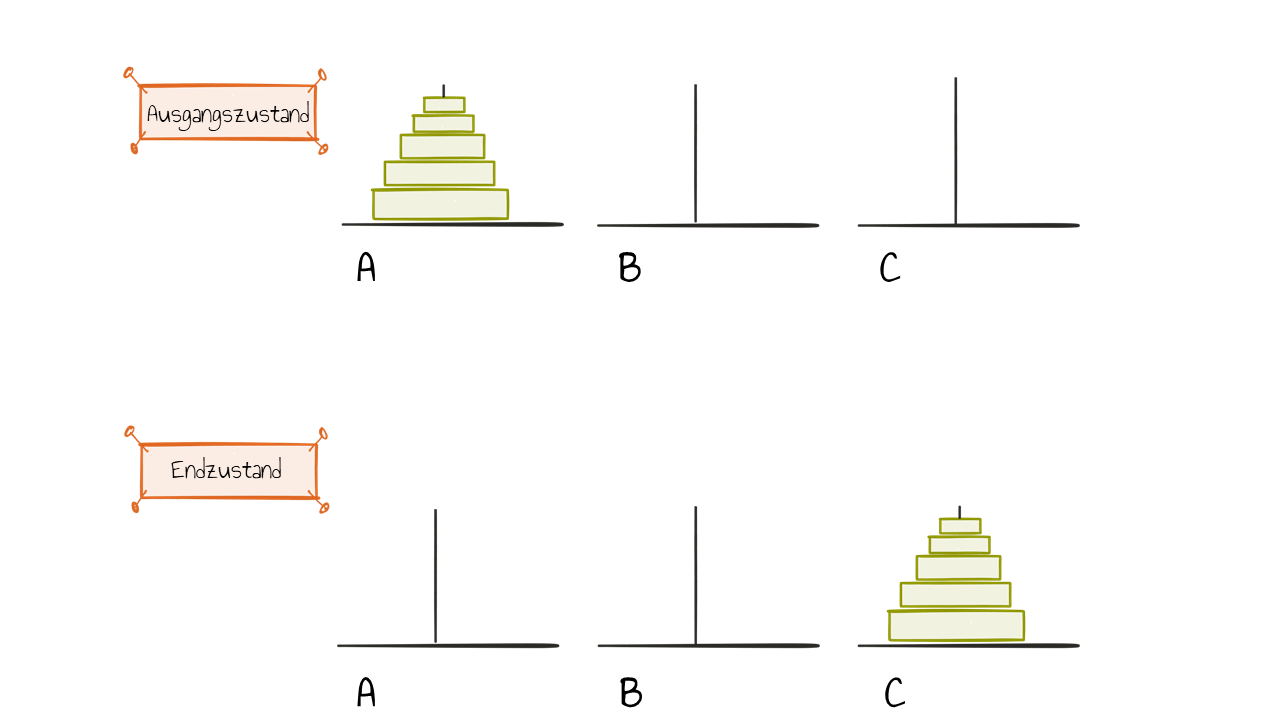
Wird die Lösung des Problems als Funktion f(A,C,B,n) beschrieben, wobei

• die erste Variable angibt, auf welchem Platz der Turm gerade liegt,
• die zweite Variable angibt, wohin der Turm soll und
• die dritte welcher Platz als Puffer verwendet werden darf.

Die letzte Variable sagt, wie viele Platten bewegt werden sollen. Die Lösung besteht dann aus folgenden Schritten

f(A,C,B,n) = {
    Ist n = 1? 
    Falls ja, lege diese eine Platte auf Platz C und 
              anschließend alle restlichen Platten von B auch auf C. 
              Sprich, führe erst f(A,C,B,1) aus und dann f(B,C,A,n-1).    
    Falls nein, lege diese obersten n-1 Platten auf den Platz B. 
                Sprich, führe f(A,B,C,n-1) aus.
}

Dies muss funktionieren, denn damit die $n$-te Scheibe auf den rechten Platz gelangen kann, müssen die $n-1$ kleineren Scheiben auf dem mittleren Platz sein.

Iterative Algorithmen

Das Prinzip der Iteration, also der Wiederholung, wird in der Mathematik verwendet, wenn keine fertigen Formeln existieren, um das gewünschte Ergebnis zu bestimmen. Diese Algorithmen besitzen eine Handlungsvorschrift, welche sich stets wiederholt. Meist wird das vorgehende Ergebnis als neuer Ausgangswert verwendet – was diese Algorithmen dann rekursiv macht. Damit die Eigenschaft der Endlichkeit gewährleistet ist, muss auch hier eine Vorschrift definiert werden, die klarstellt, wann die Wiederholungen enden. Das erfolgt meist nicht, wenn das exakte Ergebnis gefunden wurde, denn die meisten Algorithmen nähern sich nur an diesen an. Stattdessen wird das Programm beendet, wenn eine bestimmte Abbruchbedingung erfüllt ist. Oft ist diese, dass zwei aufeinanderfolgende Ergebnisse nahe zusammen liegen und keine große Änderung mehr erwartet wird.

Ein typisches Beispiel für einen iterativen Algorithmus ist das Newton-Verfahren, welches in der gymnasialen Oberstufe behandelt wird. Dieses kommt zum Einsatz, wenn Nullstellen einer Funktion bestimmt werden sollen, für die sonst keine Lösungsformeln bekannt ist, wie zum Beispiel eine Polynomfunktion $7$. Grades. Die Idee ist die folgende:

Gestartet wird mit einem beliebigen Punkt $x_{alt}$ des Funktionsgraphen einer Funktion $f$, welcher keine Extremstelle ist und anschließend wird in diesem die Tangente angelegt. Diese Tangente schneidet die $x$-Achse dann im Punkt $x_{neu}$. Als Nächstes wird die Tangente im Punkt $(x_{neu},f(x_{neu}))$ an, welche wiederum die $x$-Achse in einem neuen Punkt schneidet. An dieser Stelle wird erneut eine Tangente angesetzt.

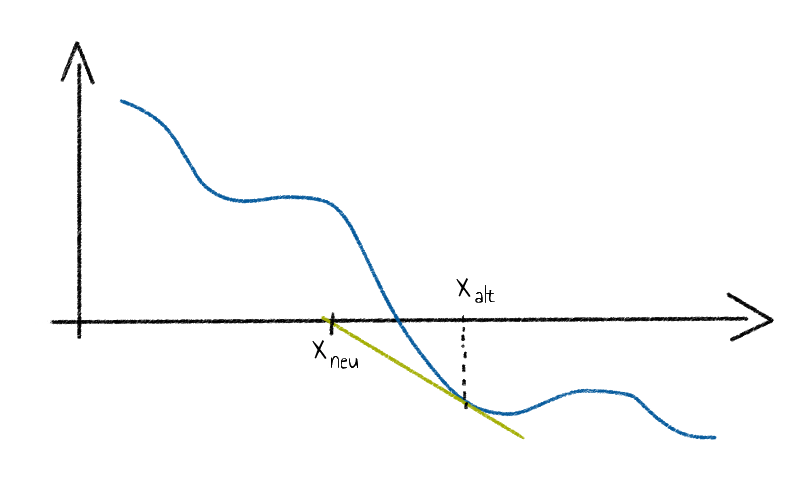
Dieses Verfahren wird dann beliebig oft durchgeführt, bis die gewünschte Annäherung erreicht wurde. Als allgemeine Formel ausgedrückt:

\[x_{neu}=x_{alt}-\frac{f(x_{alt})}{f’(x_{alt})}\]

Da das Verfahren irgendwann beendet werden muss und im Allgemeinen die Nullstelle nie genau trifft, ist ein Abbruchkriterium nötig, welches in diesem Fall lauten könnte:

Stoppe Wiederholungen, wenn sich zwei Ergebnisse betragsmäßig, um weniger als 0.0001 unterscheiden.

Zusammengefasst:

1. Es wird ein Startwert gesetzt.
2. Es wird eine Handlungsvorschrift definiert, welche aus alten Werten neue Werte ermitteln kann.
3. Es wird gestoppt, falls die gesuchte Lösung gefunden oder genug angenähert wurde. (Abbruchkriterium)

Auf ähnliche Weise funktioniert, zum Beispiel, die Intervallschachtelung, um Dezimalstellen von irrationalen Zahlen zu finden.

Dynamische Algorithmen

Dynamische Algorithmen sind dadurch gekennzeichnet, dass das zu behandelnde Problem in einfachere Teilprobleme geteilt wird (‘divide-and-conquer’ genannt) und dass Zwischenergebnisse zur späteren Verwendung gespeichert werden. Sie finden in vielen Bereichen Anwendung und nehmen unterschiedliche Form an. Darum können sie nicht so eindeutig definiert werden, wie andere Arten von Algorithmen. Zur Illustration, hier ein Beispiel:

Die Fibonacci-Folge $1,1,2,3,5,8,13,21,34…$ berechnet sich, indem die beiden letzten Folgenglieder addiert werden. Sprich,

\[f_n=f_{n-2}+f_{n-1}.\]

Als Anfangswerte werden zudem meist $f_1 = f_2 = 1$ gesetzt. Um nun zum Beispiel $f_6$ zu berechnen, muss eine Reihe Vorgänger bestimmt werden. Wird rekursiv erst $f_6 = f_5 + f_4$ eingesetzt und anschließend alle weiteren Definition der Folgenglieder, lautet das Ergebnis

\[ f_6 = (((f_2 + f_1) + f_2) + (f_2 + f_1)) + ((f_2 + f_1) + f_2).\]

Insbesondere wurde im letzten Schritt dreimal die Definition von $f_3$ verwendet. In einem Programm implementiert bedeutet das, dass der Wert $f_3$ dreimal separat berechnet wurde.

Hier ist es geschickter die Werte von unten herauf zu berechnen und zu speichern, anstatt in den Wert, der gesucht ist, alle rekursiven Formeln einzusetzen. Sprich, es wird erst $f_3 = f_2 + f_1$ berechnet und gespeichert. Anschließend wird $f_4 = f_3 + f_2$ berechnet und gespeichert. Bei der Berechnung von $f_5 = f_4 + f_3$ müssen diese Werte nun nicht mehr erneut berechnet werden, sondern es werden die bereits gespeicherten Werte von vorher benutzt.

Der wohl wichtigste positive Aspekt der dynamischen Algorithmen ist die enorme Zeitersparnis bei Problemen, bei denen bestimmte Teilprobleme mehrfach gelöst werden müssen. Ein Nachteil ist zum Beispiel der erhöhte Speicherbedarf, da eventuell viele Zwischenergebnisse gespeichert werden müssen.>

Heuristische Algorithmen

Diese Art von Algorithmen basieren nicht auf mathematischen Formeln und Gleichungen, sondern nutzen ad-hoc-Methoden, um eine Lösung schneller zu finden. Allerdings kann es dann passieren, dass die gefundene Lösung nicht optimal ist.

Ein einfaches Beispiel für einen heuristischen Algorithmus ist das Suchen des Buches „Herr der Ringe“ in einer Bibliothek. Ohne Nachzudenken kann jedes Regal abgelaufen und jedes einzelne Buch in die Hand genommen werden, um zu überprüfen, ob es das gesuchte ist. Stattdessen kann auch die folgende Heuristik verwendet werden: Es wird nur in dem Bereich der Bibliothek gesucht, in dem Fantasy-Romane stehen. Oder, noch besser: Der Bibliothekar wird nach der genauen Regalnummer gefragt. Ist das Buch allerdings falsch einsortiert, helfen diese Informationen nichts und es muss wieder auf die Ausgangsstrategie zurückgegriffen werden, die auf jeden Fall funktioniert.

Mehr Informationen zu Algorithmen finden Sie unter (Dieker & Güting, 2018).