Überblick

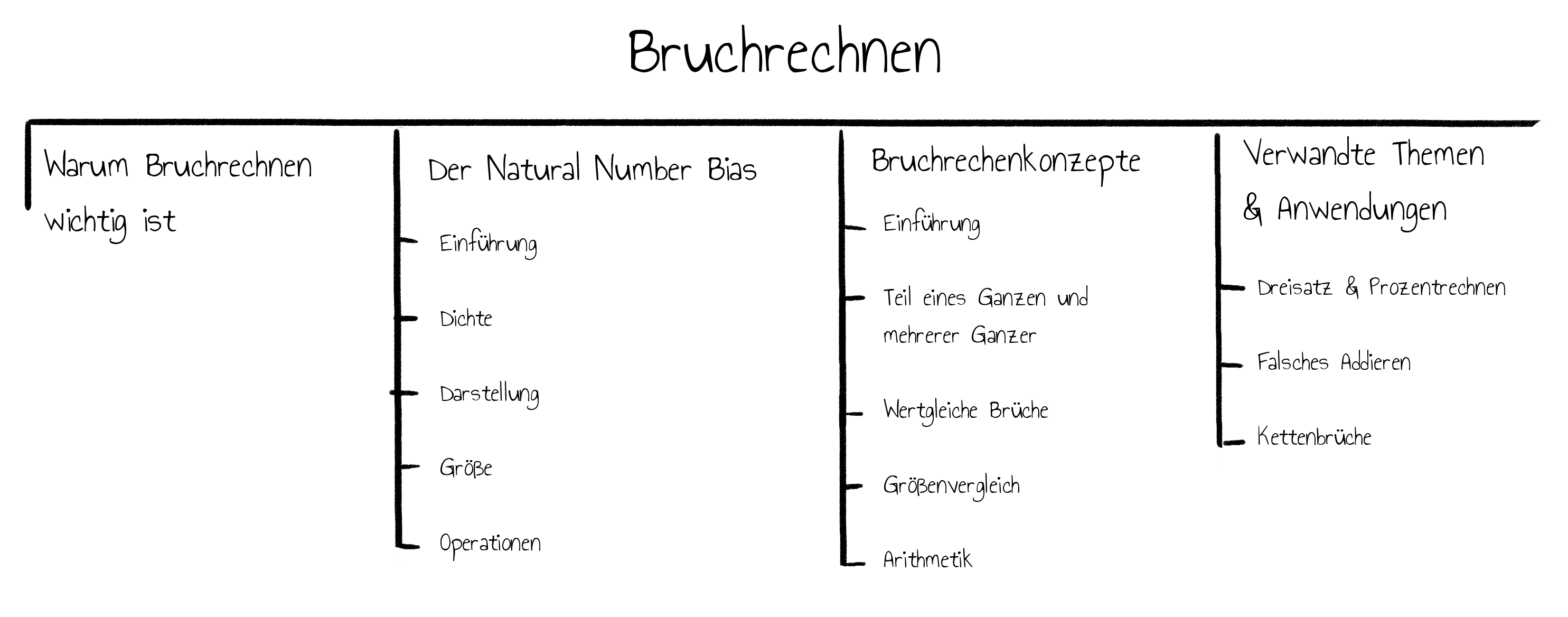
Zu Beginn dieses Modulteils wird kurz erklärt, warum ein solides Verständnis von Brüchen Grundlage für viele weitere Themen in der Mathematik ist.

Anschließend wird der Natural Number Bias vorgestellt. Dieser fasst die größten didaktischen Probleme zusammen, die entstehen, wenn von ganzen zu rationalen Zahlen gewechselt wird. Den Schwerpunkt hierbei bildet der Aspekt der “Dichte”. Er beschreibt, dass Lernende zu Anfang noch glauben, dass es immer eine nächstgrößere Zahl gibt, was bei Bruchzahlen im Gegensatz zu den ganzen Zahlen nicht mehr der Fall ist. Ein anderer Aspekt ist z.B., dass ein Bruch aus zwei Zahlen besteht, die darüber hinaus auch nicht mehr eindeutig sind. Sich diesen und anderen Verständnisproblemen bei der Vermittlung bewusst zu sein, hilft bereits, die entsprechenden Themen mit Bedacht zu behandeln.

Es folgt eine Auswahl aus fundamentalen Bruchrechenkonzepten. Hierbei liegt der Fokus auf Konzepten, die sich durch anschauliche, handlungsorientierte Überlegungen herleiten und erklären lassen. Die Grundideen werden eingeführt, wenn Brüche als Teil eines Ganzen oder Teil mehrerer Ganzer vorgestellt werden. Diese ziehen sich dann durch die folgenden Abschnitte: Wertgleiche Brüche, Größenvergleich und Arithmetik.

Danach werden drei Situationen präsentiert, in denen Bruchrechnen eine Rolle spielt. Sie gehen allerdings über den Stoff der sechsten Klasse hinaus, in der die Bruchrechnung üblicherweise behandelt wird. Sie treten aber z.B. im Physikunterricht auf und können auch in Seminaren in der Oberstufe behandelt werden.

Am Ende finden Sie Aufgaben für das Selbststudium, eine Liste der verwendeten Literatur und Aufgaben für den Schulunterricht.