Warum Bruchrechnen wichtig ist

(Bailey, Hoard, Nugent & Geary, 2012; Obersteiner, Van Hoof & Verschaffel, 2013; Vamvakoussi, Van Dooren, & Verschaffel, 2012; Yamagishi,1997)

Bruchrechnen ist ein grundlegendes Konzept der Mathematik. Das Verständnis für die Bruchrechnung steht in engem Zusammenhang mit dem Verständnis komplexerer Themen (Bailey, Hoard, Nugent & Geary, 2012). Darüber hinaus können Fehlvorstellungen zu Brüchen und deren Beziehungen im Alltag zu Fehleinschätzungen führen (vgl. Yamagishi, 1997). Fehlvorstellungen zu Brüchen manifestieren sich dabei insbesondere nicht nur bei Kindern und Jugendlichen, sondern auch bei Erwachsenen mit viel Erfahrung im Bruchrechnen (Obersteiner, Van Hoof & Verschaffel, 2013). Die Art der Fehler, die dabei auftreten, sind zum Großteil systematisch und lassen sich auf den sogenannten Natural Number Bias (Vamvakoussi, Van Dooren, & Verschaffel, 2012) zurückführen: Viele halten fälschlicherweise an Konzepten fest, die für natürliche Zahlen gelten, aber nicht mehr für rationale Zahlen. Dieser Bias wird im nächsten Abschnitt ausführlich behandelt.

Neben handwerklichen und technischen Anwendungen – wie etwa die Bestimmung der Länge von Klaviersaiten oder von Übersetzungsverhältnissen bei Getrieben – stellt die Bruchrechnung auch das Fundament für viele weitere Themen im Unterricht selbst dar, sowohl an der Schule als auch an der Hochschule. Beispiele für solche Themen sind unter anderem:

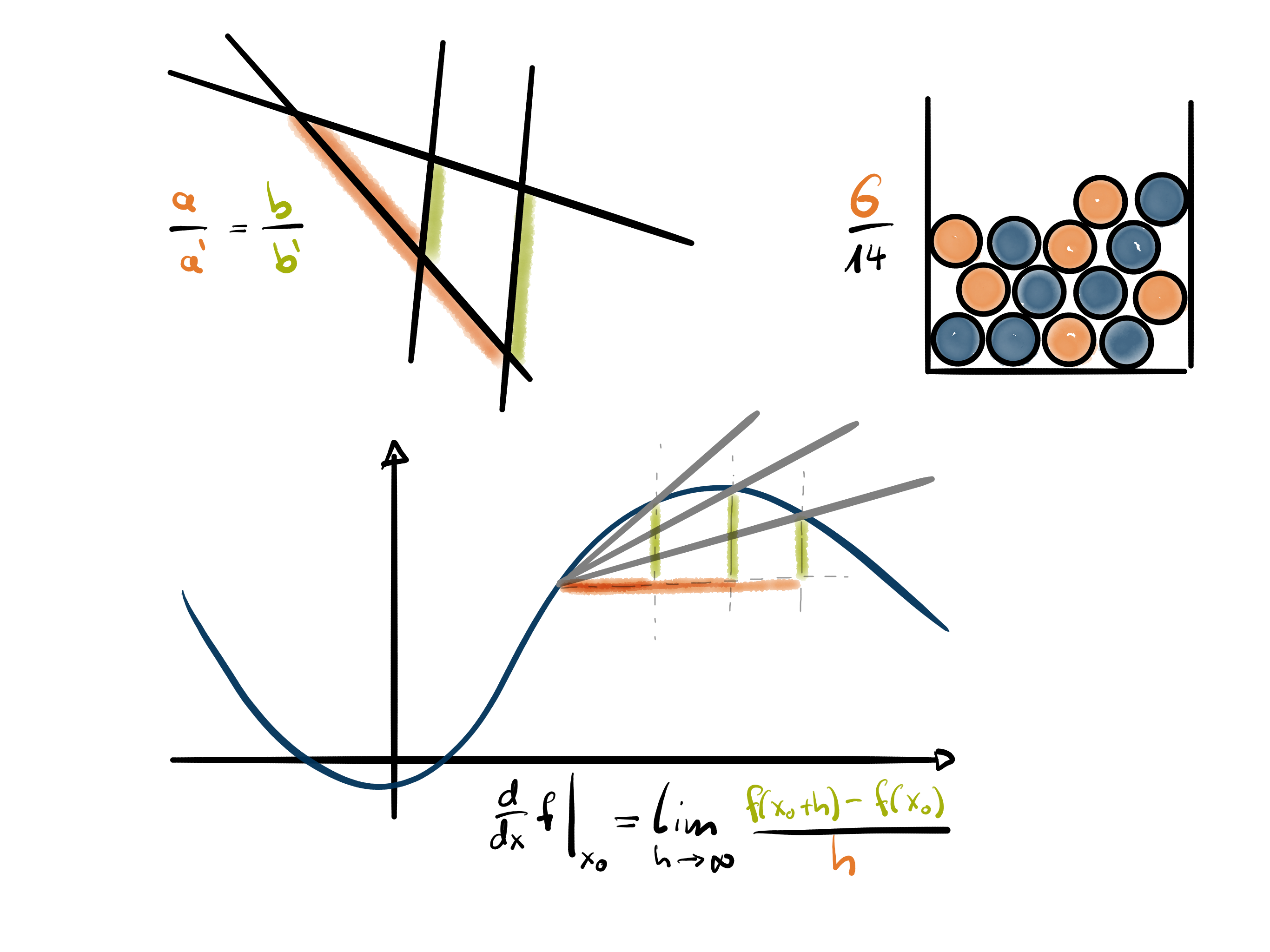
• Der Strahlensatz in der Geometrie
• Relative Häufigkeiten in der Stochastik
• Gebrochen-rationale Funktionen und die Definition von Ableitungen in der Kurvendiskussion
• Bedingte Wahrscheinlichkeiten in der Wahrscheinlichkeitsrechnung
• Das Lösen von linearen Gleichungen in der linearen Algebra
• Bei Proportionalitätsaussagen in der Physik wie z.B. dem Ohm’schen Gesetz oder der thermischen Zustandsgleichung idealer Gase
• Das Modulo-Rechnen in der Zahlentheorie
• Der Umgang mit endlichen Körpern und das Lokalisieren nullteilerfreier Ringe in der (kommutativen) Algebra

Ohne ein gutes Verständnis von grundlegenden Bruchrechenkonzepten ist es schwierig, komplexere und höhere Fragestellungen adäquat behandeln zu können. Alleine aus diesem Grund lohnt es sich, auch in höheren Klassen die Grundlagen des Bruchrechnens zu wiederholen, insbesondere in Vorbereitungskursen für Berufs- oder auch Hochschulen.