Wertgleiche Brüche

Werden Brüche wie im vorhergehenden Abschnitt über Diagramme eingeführt, so haben die Lernenden meist schon bemerkt, dass unterschiedliche Brüche gleiche Anteile darstellen können. Werden Brüche auf dem Zahlenstrahl behandelt, passiert das erneut. Das führt dann fast selbstverständlich zu der Frage, wie diese wertgleichen Brüche zusammenhängen und leitet in der Folge zum Konzept des Erweiterns und Kürzens über. Erweitern und Kürzen wird dadurch nicht als abstrakte Operation auf zwei Zahlen – Zähler und Nenner – eingeführt, sondern als geometrische Notwendigkeit.

Das kann im Unterricht zusätzlich dadurch betont werden, dass ein Hefteintrag, ein Arbeitsblatt oder andere Arbeitsmittel nicht unter der Überschrift “Erweitern und Kürzen” steht, sondern unter “Wertgleiche Brüche”. Wertgleiche Brüche sind das Phänomen, Erweitern und Kürzen hingegen dient nur als Werkzeug, um es zu verstehen.

Dafür bietet sich ein handlungsorientierter Ansatz an, bei dem Lernende wertgleiche Brüche identifizieren sollen und dabei selbstständig Regeln entwickeln, wann diese auftreten. Ein Beispiel dafür ist die folgende interaktive Aufgabe aus dem ALICE eBook.

Anleitung: Tippen Sie drei Kreise an, die dieselbe Bruchzahl darstellen. Ein weiter Klick auf einen ausgewählten Kreis hebt die Auswahl wieder auf.

Diese Aufgabe wird in Szene 02: Gruppenarbeit von einer der drei Gruppen bearbeitet. Den entsprechenden Ausschnitt dieser Szene sehen Sie unten. Die Schülerinnen dieser Gruppe können hier gleichzeitig mit ikonischen und symbolischen Darstellungen arbeiten und diese miteinander vergleichen.

Da es sich um eine Wiederholungsstunde handelt, wurde der Aufgabe ein Warnton hinzugefügt, der vom stupiden Ausprobieren abhalten soll. Dieselbe Aufgabe kann allerdings auch zur Exploration verwendet werden. Dann muss der Warnton abgeschaltet werden, wie nach dem Video noch erläutert wird.

Wie oben bereits angerissen, kann der Warnton im Video ausschließlich für Übungssituationen genutzt werden. Schülerinnen und Schüler – vor allem in der sechsten Klasse, in der das Bruchrechnen eingeführt wird – können in der Erarbeitungs- beziehungsweise Lernphase dadurch stark demotiviert werden.

Für Übungszwecke kann dieses instrument allerdings hilfreich sein, um “den Einsatz zu erhöhen”. Insbesondere bei Grundlagen wie dem Einmaleins oder wie hier dem Bruchrechnen ist es durchaus das Ziel, schnell und korrekt rechnen zu können ohne Ausprobieren zu müssen.

Wie im Video zu sehen, kann die Klasse mittels Gruppenarbeit oder Lehrer-Schüler-Gespräch dahin geführt werden, zu erkennen, dass wertgleiche Brüche sich nur durch eine Verfeinerung oder Vergröberung der Einteilung ergeben, welche durch den Nenner gegeben ist.

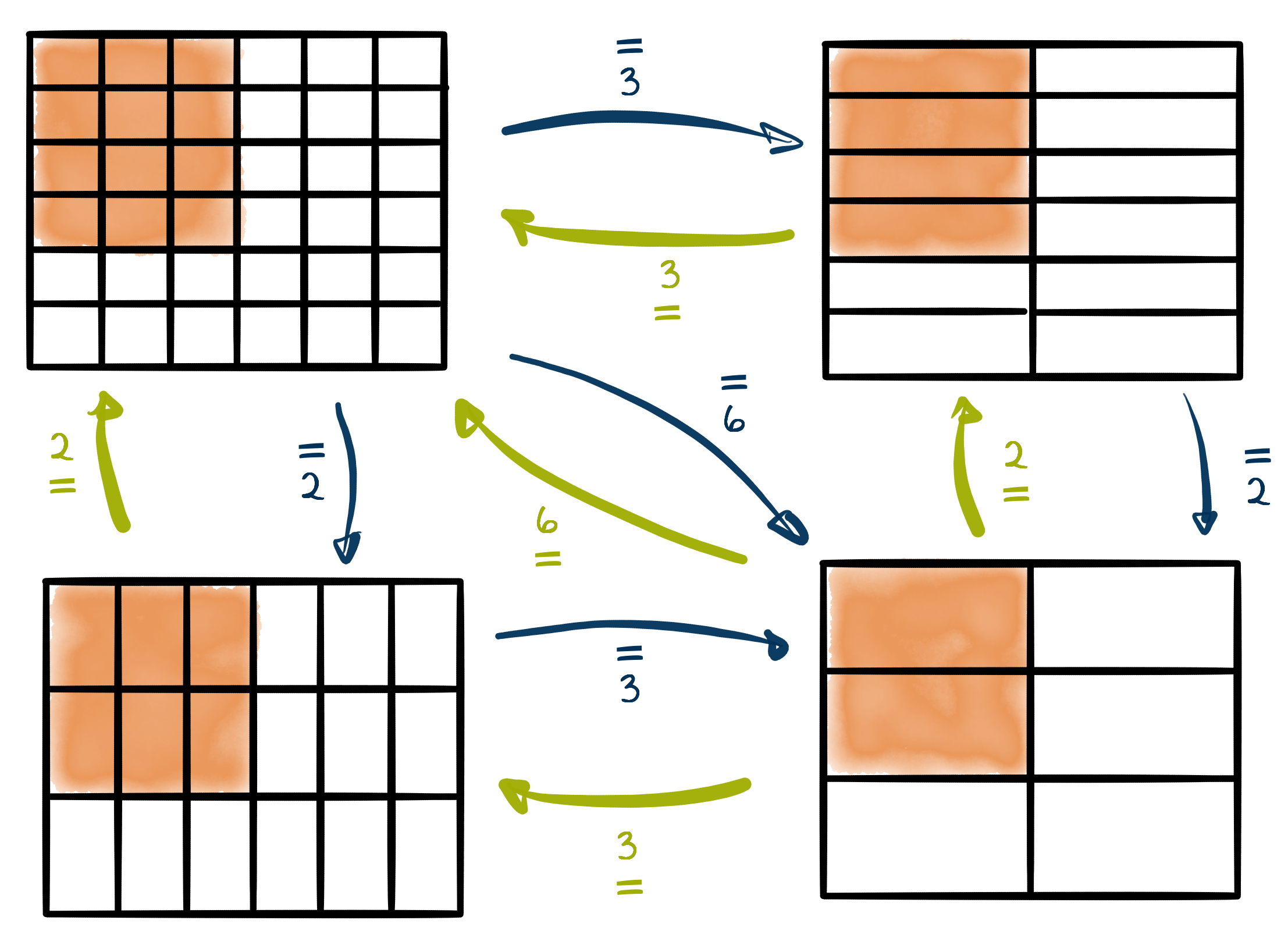
Hierbei wird die Konvention verwendet, dass eine Zahl über dem Gleichheitszeichen angibt, dass mit ihr erweitert wurde; unter dem Gleichheitszeichen, dass gekürzt wurde.

\[\frac{2}{6}\enspace \overset{\small 2}{=}\enspace \frac{4}{12}\qquad\text{ und }\qquad \frac{4}{12}\enspace \underset{\small 2}{=}\enspace \frac{2}{6}.\]

Die Beziehung wertgleicher Brüche kann an dieser Stelle vertieft und geübt werden, ohne darauf eingehen zu müssen, wie Zähler und Nenner sich dabei numerisch verändern. Die Operation “mit $3$ erweitern” wird dabei umgesetzt als “die Einteilung dreimal so fein machen”.

Das Kürzen folgt demselben Prinzip. Erst nachdem die Begriffe Erweitern und Kürzen als Veränderung der Einteilung gefestigt wurden, sollte auf Zähler auf Nenner eingegangen werden. So kann verhindert werden, dass die Lernenden diese Operationen als “oben und unten das Gleiche machen” verinnerlichen und, insbesondere, Fehler vermeiden wie z.B. im Zähler und Nenner dieselbe Zahl zu addieren. Wie Zähler und Nenner als Zahlen manipuliert werden müssen, ist in dieser Art der Vermittlung eine reine Konsequenz aus der anschaulichen geometrischen Manipulation des Bruches. Diese Idee wird sich durch alle weiteren Aspekte der Bruchrechnung ziehen, die hier im Laufe des Moduls noch besprochen werden.

Um zu motivieren, dass eine Rechenregel überhaupt gebraucht wird, können Lehrkräfte mit den Lernenden komplexere Brüche mit größeren und unanschaulicheren Zählern und Nenner behandeln. Geschieht das dann auch noch mit physischem Anschauungsmaterial, können Lernende ganz konkret erfahren, dass nicht nur die Vorstellungskraft an ihre Grenzen kommt, sondern auch reale Hilfsmittel. Das ist in Szene 3: Arbeit mit Materialien zu sehen, in der die Lernenden von alleine merken, dass nicht jeder Bruch mit jeder Methode dargestellt werden kann.

Wie im Abschnitt Teil eines Ganzen und Teil mehrerer Ganzer zuvor können Aufgaben zu wertgleichen Brüchen variiert werden, indem eine das Ganze nicht vorunterteilt wird. So wird auch hier die Intuition der Lernenden gestärkt. In dieser Variante, ebenso aus dem ALICE eBook, sieht die Aufgabe aus dem Unterrichtsvideo wie folgt aus.

Anleitung: Tippen Sie drei Kreise an, die dieselbe Bruchzahl darstellen. Ein weiter Klick auf einen ausgewählten Kreis hebt die Auswahl wieder auf.

Diese Aufgabe im Speziellen wird dadurch ungemein schwieriger – nicht zuletzt da hier die Brüche zufällig generiert werden. Deswegen sollte sie eher sporadisch eingesetzt werden und nur zur Ergänzung der anderen Aufgaben dienen. Dies trifft im Wesentlichen auf alle Aufgaben zu, die in dieser Form abgewandelt wurden.