Teil eines Ganzen und mehrerer Ganzer
(Robertson & Webb, 1998)
Der Hauptzweck von Brüchen und Bruchzahlen ist es, Anteile von ganzen Einheiten darzustellen. Dabei gibt es zwei Interpretationen, die zu demselben Ergebnis führen.
Möglichkeit 1: Es ist ein Ganzes gegeben, welches in gleichgroße Teile geteilt wird. Von diesen Teilen wird dann eine bestimmte Anzahl ausgewählt.

Möglichkeit 2: Es wird eine Anzahl mehrerer Ganzer betrachtet, die anschließend fair aufgeteilt werden.
Auch wenn beide Sichtweisen prinzipiell äquivalent sind, ermöglichen sie je nach Anwendungsgebiet leichtere und leichter verständliche Rechnungen.
Als Teil eines Ganzen beschreibt ein Bruch $\frac{a}{b}$, dass das Ganze – eine Pizza, ein Geldbetrag, ein Holzbalken, ein Stapel Bücher, die Menge Wasser in einer Flasche etc. – in $b$ gleichgroße Teile geteilt wird, von denen anschließend $a$ Stück ausgewählt werden:
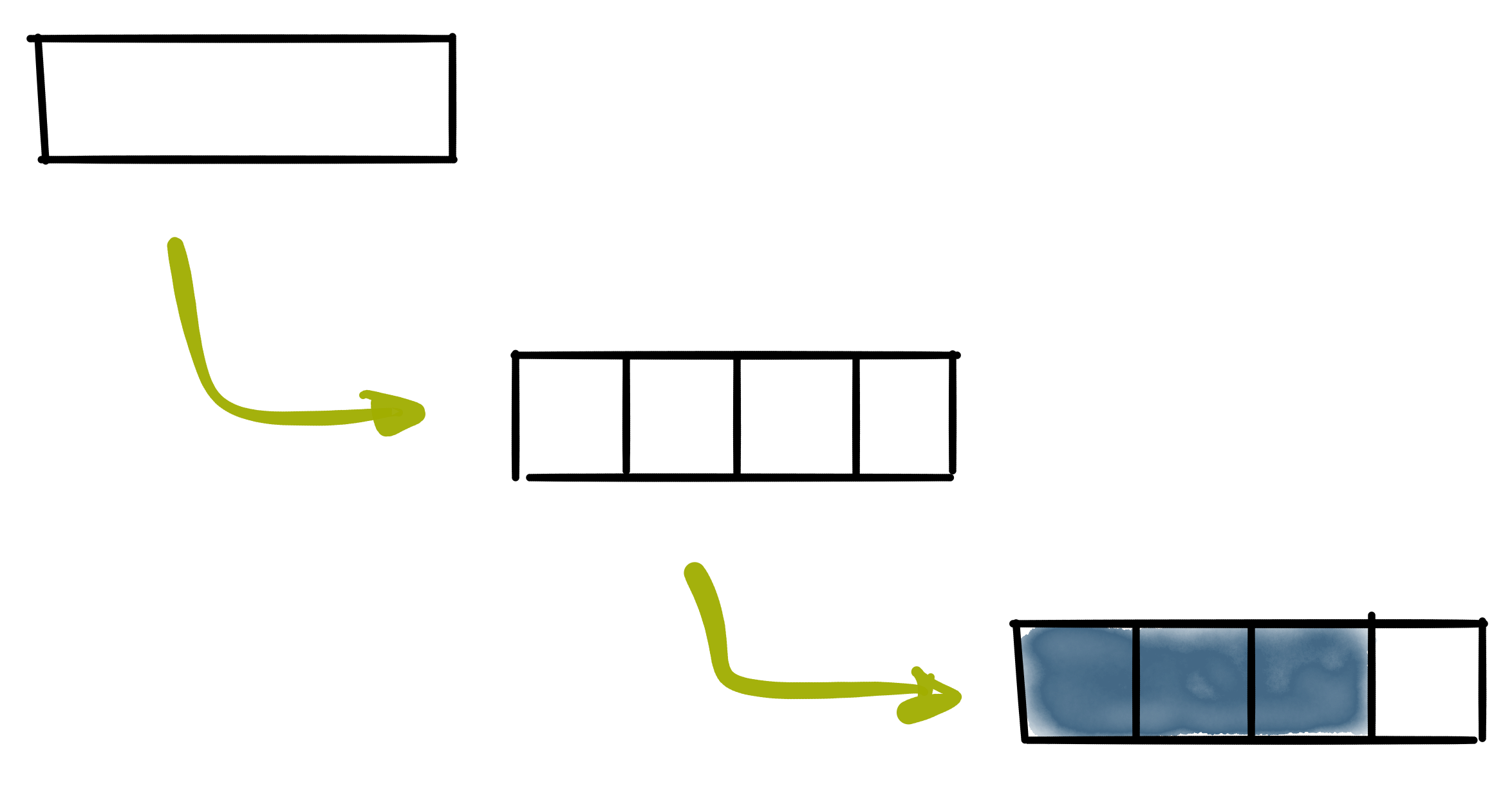
$\frac{3}{4}$ sind drei Viertelstücke eines Ganzen. Somit gibt es immer eine Bezugsgröße, mit der verglichen wird.
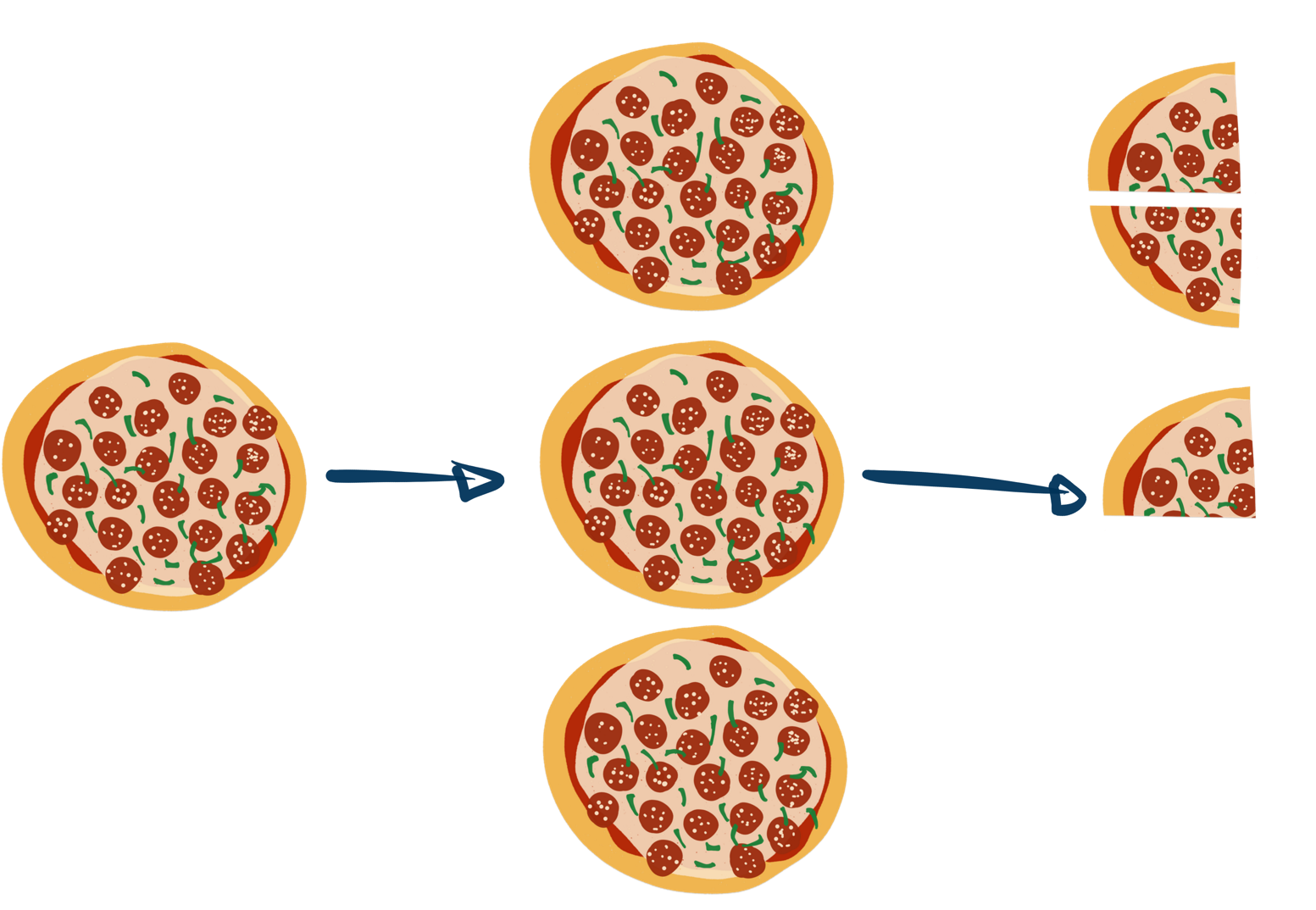
Als Teil mehrerer Ganzer beschreibt derselbe Bruch, dass $a$ Stück Ganze gemeinsam betrachtet und auf $b$ Teile aufgeteilt werden:
$\frac{3}{4}$ sind ein Viertel von drei Ganzen.
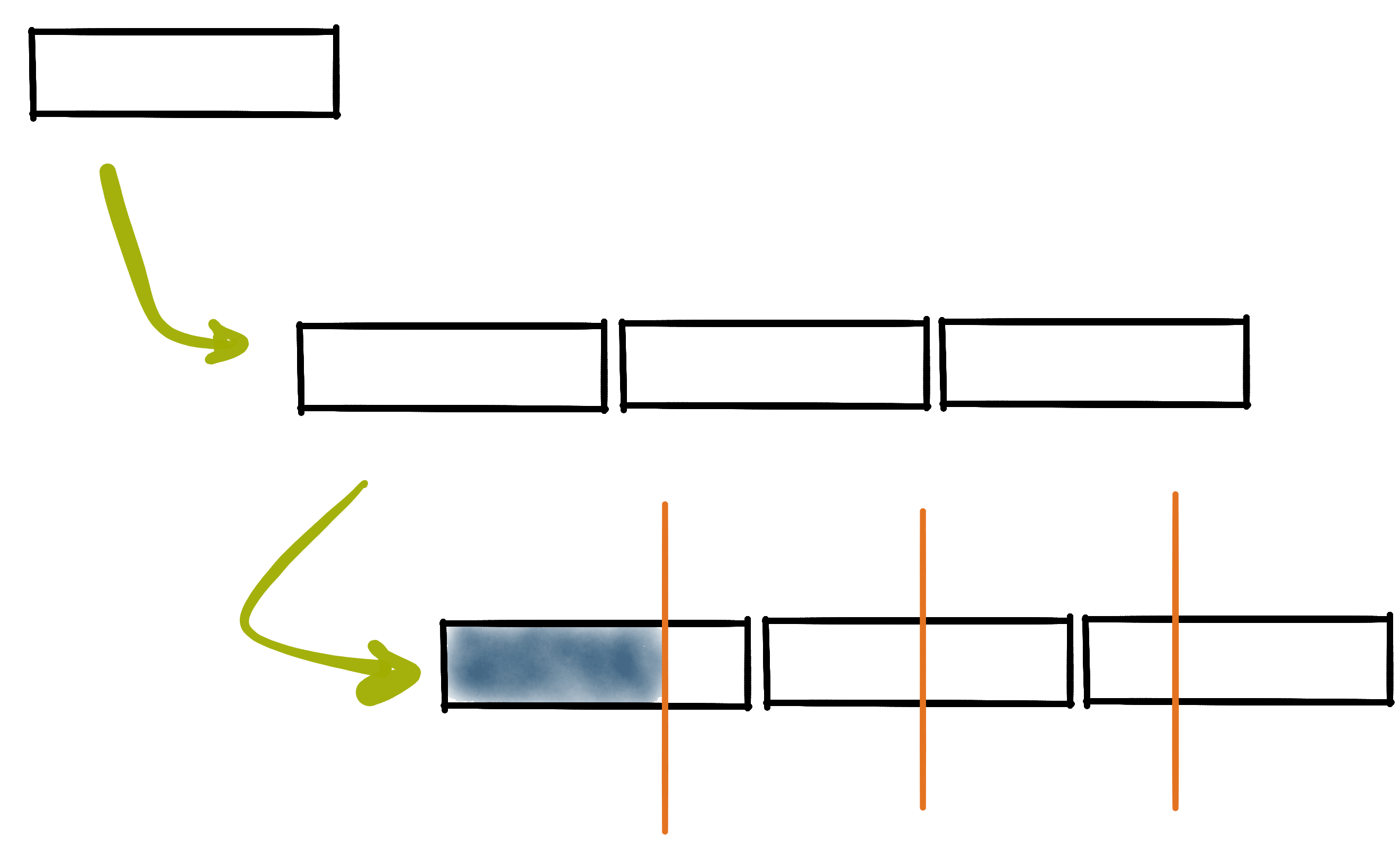
Für die Berechnung von Anteilen bedeutet dies, dass die Reihenfolge umgekehrt wird, in der Zähler und Nenner auf ein Ganzes angewandt werden. Wird z.B. danach gefragt, was $\frac{3}{4}$ von $180\,\text{€}$ sind – etwa bei einer Rabattaktion – so ergeben sich die folgenden beiden Rechnungen: Als Teil eins Ganzes werden die $180\,\text{€}$ erst in $4$ Teile zu je $45\,\text{€}$ geteilt, von denen dann $3$ zusammen $135\,\text{€}$ ergeben.
\[\frac{3}{4}\text{ von }180\,\text{€}\enspace =\enspace 3 \cdot (180\,\text{€} : 4)\enspace =\enspace 3\cdot 45\,\text{€}\enspace =\enspace 135\,\text{€}.\]
Als Teil mehrerer Ganzer werden hingegen erst $3$ Vielfache der $180\,\text{€}$ betrachtet, die $540\,\text{€}$ ergeben, und diese werden anschließend durch $4$ geteilt, um die $135\,\text{€}$ zu erhalten.
\[\frac{3}{4}\text{ von }180\,\text{€}\enspace =\enspace (3 \cdot 180\,\text{€}) : 4\enspace =\enspace 540\,\text{€} : 4\enspace =\enspace 135\,\text{€}.\]
Zu beachten ist, dass die Rollen von Zähler und Nenner sich nicht geändert haben: Der Zähler gibt in beiden Fällen an, wie viel genommen wird, der Nenner beide Male in wie viele Teile zerteilt wird.
Und selbst wenn es jedem mit ein bisschen Erfahrung im Bruchrechnen klar ist, dass die beiden Rechnungen oben das selbe Ergebnis liefern, so ist das für Lernende, die sich mit dieser Thematik neu auseinandersetzen, durchaus nicht selbstverständlich. Das führt zu der Frage, warum es überhaupt notwendig ist, beide Interpretationen einzuführen. Ein Grund hierfür ist, dass beide direkt in der Praxis Anwendung finden. Um im Beispiel vom Verteilen von Pizzen zu bleiben:
- Es kann sein, dass bei einer Party zwei Leute je $\frac{4}{8}$ einer Pizza wollen $\longrightarrow$ Teil eines Ganzen.
- Aber genauso kann es sein, dass $4$ ganze Pizzen an $8$ Leute verteilen werden sollen $\longrightarrow$ Teil mehrerer Ganzer.
Weiterhin gibt es Situationen, die mit der Interpretation Teil eines Ganzen nicht direkt gelöst werden können: Im folgenden Ausschnitt von Szene 4: Präsentation der Ergebnisse erläutert der Schüler die Problematik, nachdem seine Gruppe versucht hat, verschiedene Brüche mit Legosteinen darzustellen.
Besteht die gegebene Darstellungsart – wie im Videoausschnitt gezeigt – aus atomaren Bauteilen, so wird dadurch eingeschränkt, welche Brüche darstellbar sind. Wird z.B. nach $\frac{4}{6}$von $15$ gefragt, so ist es per se nicht möglich die $15$ gegebenen Stücke durch $6$ zu teilen; zumindest nicht, wenn die Lernenden gerade erst am Anfang des Themas sind.
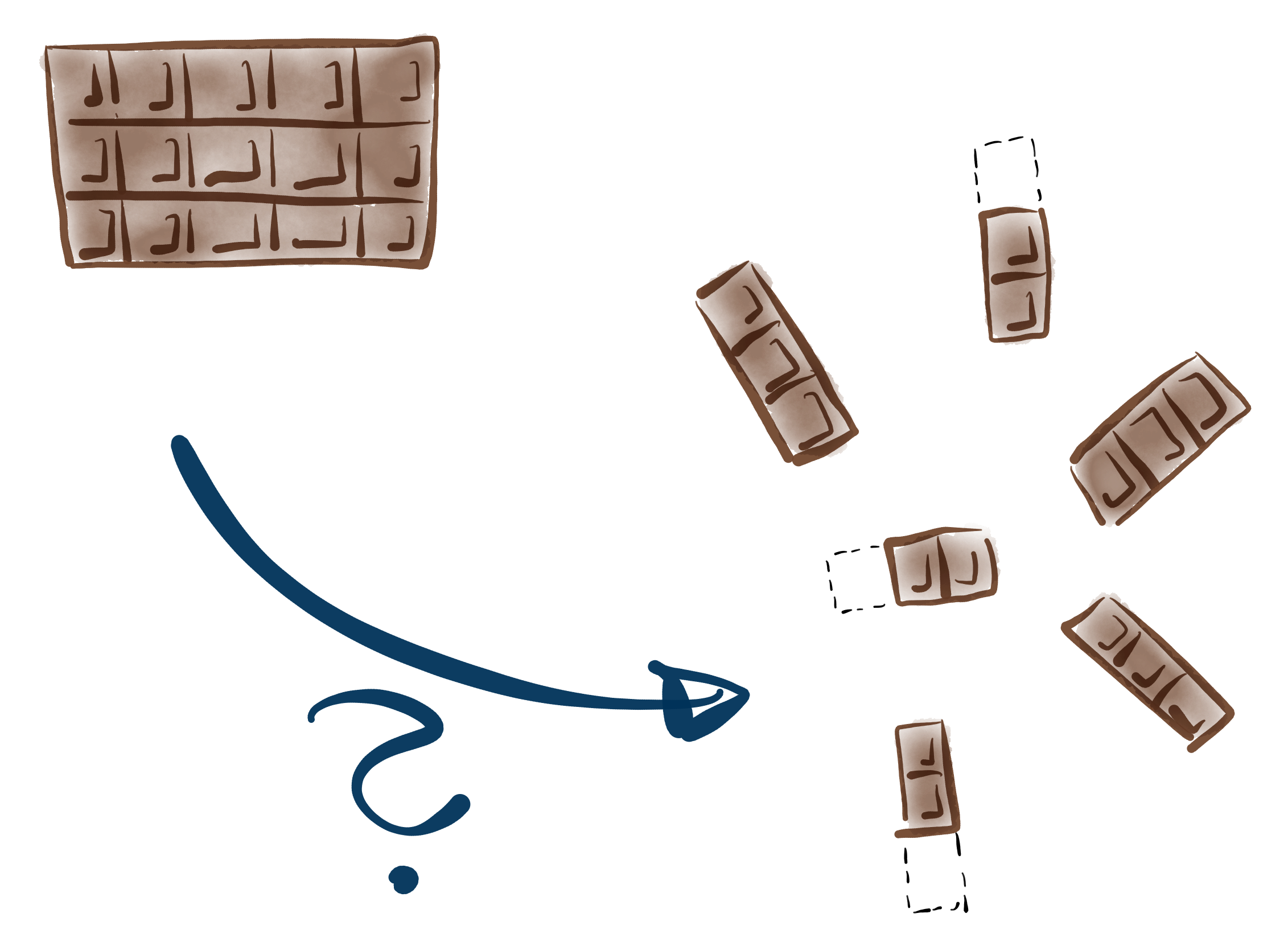
So ist es zwar möglich $15 : 6$ als $\frac{15}{6}$ zu schreiben und anschließend mit $4$ zu multiplizieren oder alternativ $\frac{4}{6}$ zu $\frac{2}{3}$ zu kürzen, was aber gewisse Kenntnisse in der Bruchrechnung voraussetzt. Die Interpretation Teil mehrerer Ganzer läuft hier aber ohne Weiteres durch:
\[\frac{4}{6}\text{ von } 15\enspace =\enspace (4\cdot 15) : 6\enspace =\enspace 60 : 6\enspace =\enspace 10.\]
Es werden also verschiedene Konzepte gebraucht.
Andererseits gibt es auch Vorteile der Anschauung Teil eines Ganzen gegenüber Teil mehrerer Ganzer: Sieht man einen Bruch als Teil eines Ganzen, wird sofort klar, was ein unechter Bruch mit $a > b$ darstellt. Da mehr Stücke gewählt werden sollen als vorhanden sind, muss dieser Bruch mehr als ein Ganzes darstellen. Als Teil mehrerer Ganzer sind unechte Brüche schwieriger zu fassen, denn die Aufgabe, $3$ Pizzen gleichmäßig auf $4$ Personen zu verteilen, unterscheidet sich als Handlung nicht davon, $5$ Pizzen auf dieselben Personen zu verteilen. Dass $\frac{5}{4}$ unecht ist, schlägt sich hier nur in der Konsequenz nieder, dass jede Person am Ende mehr als eine volle Pizza bekommt.
Das bereits beschriebene Problem bei der Bestimmung von $\frac{4}{6}$ von $15$, das es notwendig gemacht hat, die Interpretation Teil mehrerer Ganzer zu verwenden, bestand darin, dass $15 : 6$ anfangs nicht direkt bestimmt werden kann. Nun gibt es aber Fälle, in denen das Ausweichen auf Teil mehrerer Ganzer auch nicht hilft; z.B. wenn nach $\frac{4}{7}$ von $15$ gefragt ist. Dann wird es definitiv nötig, die eigentlich atomaren Teile weiter zu zerteilen. Bei Gegenständen wie einer Schokoladentafel ist das an sich kein Problem, bei einer Handvoll Münzen schon eher. Dies führt dann zu Dezimalbrüchen, zu feineren Unterteilungen, zum Erweitern und Kürzen, und zur Frage, wie Brüche mit natürlichen Zahlen multipliziert werden können. Die letzten beiden Themen werden in den folgenden Abschnitten behandelt.
Ein verwandtes Problem beider Darstellungen besteht darin, dass bei an sich stetigen Objekten wie einer Pizza zwar prinzipiell jede Stückelung möglich wäre, es aber praktisch unmöglich ist, diese ganz genau zu erzielen. Dieses Thema wird z.B. im Buch Cake Cutting Algorithms von Robertson und Webb (1998) behandelt. Für den Umfang dieses Moduls – und auch für die Behandlung der Bruchrechnung im Schulunterricht – kann immer davon ausgegangen werden, dass solche Ein- und Zerteilungen zweckmäßig sind. Dennoch kann es sich lohnen, über die Problematik zu sprechen, falls die nötige Zeit und Ressourcen es erlauben bzw. wenn die Schülerinnen und Schüler es ansprechen.
In leicht abgewandelter Form kann diese Fragestellung nach nur geschätzten Unterteilungen allerdings sehr hilfreich sein, um bei Lernenden ein intuitives Verständnis von Brüchen zu schaffen. Eine Standardaufgabe zum Erlernen des Bruchrechenbegriffs ist die folgende aus dem ALICE-eBook.
Link zur Originalversion
Anleitung: Markieren Sie durch Tippen auf die Kreissegmente den gegebenen Bruch. Klicken Sie zum Überprüfen Ihrer Antwort auf den orangefarbenen “Stimmt das?”-Knopf. Zum anschließenden Anzeigen einer neuen Aufgabe klicken Sie auf den blauen “Neue Aufgabe”-Knopf.
Da der Nenner durch die Einteilung schon eingezeichnet ist, trainiert sie mehr das Verständnis des Zählers. Außerdem vermittelt sie kein Größenverständnis der Brüche, denn beispielsweise bei sowohl $\frac{3}{4}$ als auch $\frac{3}{10}$ müssen $3$ Stücke abgezählt werden. Für die Einführung von Brüchen sind Aufgaben dieser Art zwar natürlich unabdingbar. Sie können aber auch noch zusätzlich durch Aufgaben der folgenden Art ergänzt werden.
Link zur Originalversion
Anleitung: Markieren Sie den gegebenen Bruch so genau wie möglich. Klicken Sie zum Überprüfen Ihrer Antwort auf den orangefarbenen “Stimmt das?”-Knopf. Zum anschließenden Anzeigen einer neuen Aufgabe klicken Sie auf den blauen “Neu”-Knopf.
Ohne vorgegebene Unterteilung ist es hier notwendig, den Zusammenhang zwischen Zähler und Nenner verstanden zu haben. Das kann zu Erkenntnissen führen wie
” $\frac{3}{5}$ ist ein bisschen größer als $\frac{1}{2}$ “
oder auch
” $\frac{7}{12}$ ist einfach nur 7 Uhr”.
Dadurch dass die einzelnen Teilaufgaben der Anwendung in rascher Folge bearbeitet werden können und die Brüche nicht pixelgenau getroffen werden müssen, wiegen Fehler weniger schwer. Diese Aufgabe dient somit mehr als Experimentierfeld zum Ausprobieren denn als Leistungskontrolle. Das Einstreuen solcher Arbeitsaufträge in den Bruchrechenunterricht kann so besser auf die nachfolgenden komplexeren Konzepte vorbereiten: Erkenntnisse, wie etwa die Tatsache, dass $\frac{2}{3}$ und $\frac{4}{6}$ an derselben Stelle liegen, fallen stärker ins Auge, wenn keine Einteilung vorgegeben ist. Dieses Beispiel ist relevant für das Verständnis von Erweitern und Kürzen sowie vom Zahlenstrahl.
Abschließend soll hier noch eine weitere Interpretation von Brüchen vorgestellt werden, die im weiteren Verlauf des Moduls hauptsächlich angewandt wird: Da der Nenner die Größe eines (An-)Teils beschreibt, kann der zugehörige Stammbruch als abstrakte Einheit “Stück” aufgefasst und verwendet werden. So besteht dann kein Unterschied mehr zwischen $3\,\text{€}$, $3\,\text{m}$, $3$ Stück und etwa $\frac{3}{4}$. Dadurch werden Zähler und Nenner noch stärker entkoppelt und ihre unterschiedlichen Rollen noch stärker betont: Der Nenner benennt die Größe der Stücke und der Zähler zählt die Anzahl der Stücke.
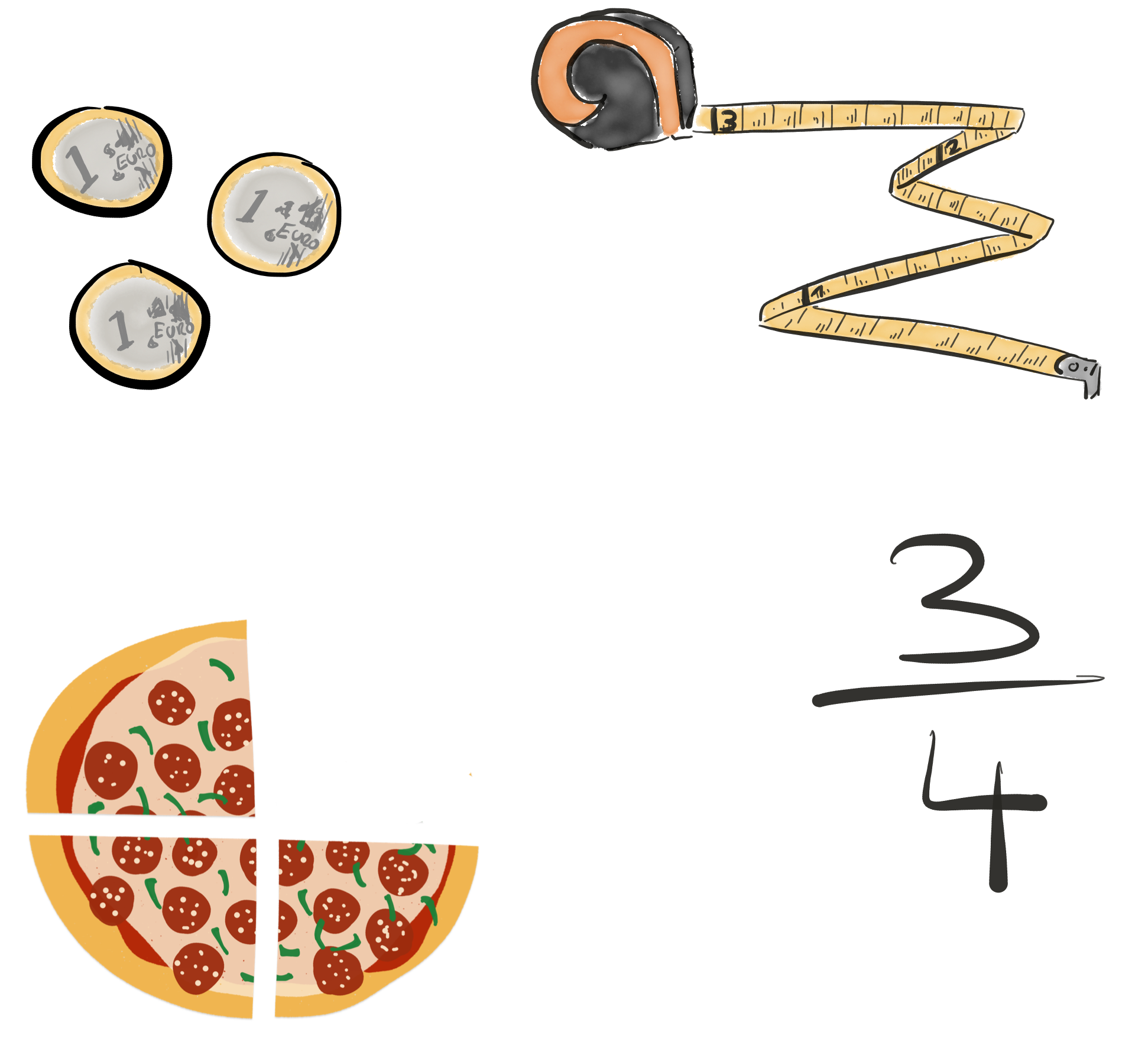
Prinzipiell unterscheidet sich diese Anschauung nicht von der Anschauung Teil eines Ganzen. Nur wird das Ganze in den Hintergrund gerückt, da die exakte Größe der Stücke ignoriert wird. Dieses Vorgehen reduziert allerdings die Komplexität eines Bruches und eignet sich hervorragend für einfache weiterführende Fragen wie z.B. die Frage, wie Brüche mit natürlichen Zahlen multipliziert werden können. Und auch bei anderen Bruchrechenkonzepten wird sich diese Interpretation im Folgenden als Schlüssel zum Verständnis herausstellen.