Bruchrechenkonzepte

Aufgaben 5-8

Aufgabe 5

Ein Problem, das auftritt, wenn das Zerteilen von Pizzen oder Schokoladentafeln herangezogen wird, um Brüche einzuführen, ist, dass es nicht klar ist, wie diese Ganzen denn in tatsächlich gleichgroße Teile geteilt werden können. Falls diese Diskussion im Unterricht aufkommt, kann die folgende Fragestellung helfen, über dieses Problem nachzudenken:

Gegeben sei eine Pizza, die sich Yusuf und Annika teilen wollen. Wie können die beiden die Pizza fair untereinander aufteilen, wenn ihnen der Belag gleich gut schmeckt und die Pizza gleichmäßig belegt ist?

Klicken Sie die richtige Antwort an.

Aufgabe 6

Gegeben sein ein Quadrat mit Seitenlänge 1. In dieses wird der Kreis einbeschrieben, der alle Seiten berührt. In diesen Kreis wird ein neues Quadrat eingezeichnet, welches seitenweise parallel zum äußeren ist und dessen Ecken auf dem Kreisrand liegen. Dieser Prozess wird nun im inneren Quadrat noch einmal wiederholt, sodass die unten zu sehende geschachtelte Figur aus drei Quadraten und zwei Kreisen entsteht. Wie groß ist die Fläche des innersten Quadrats?

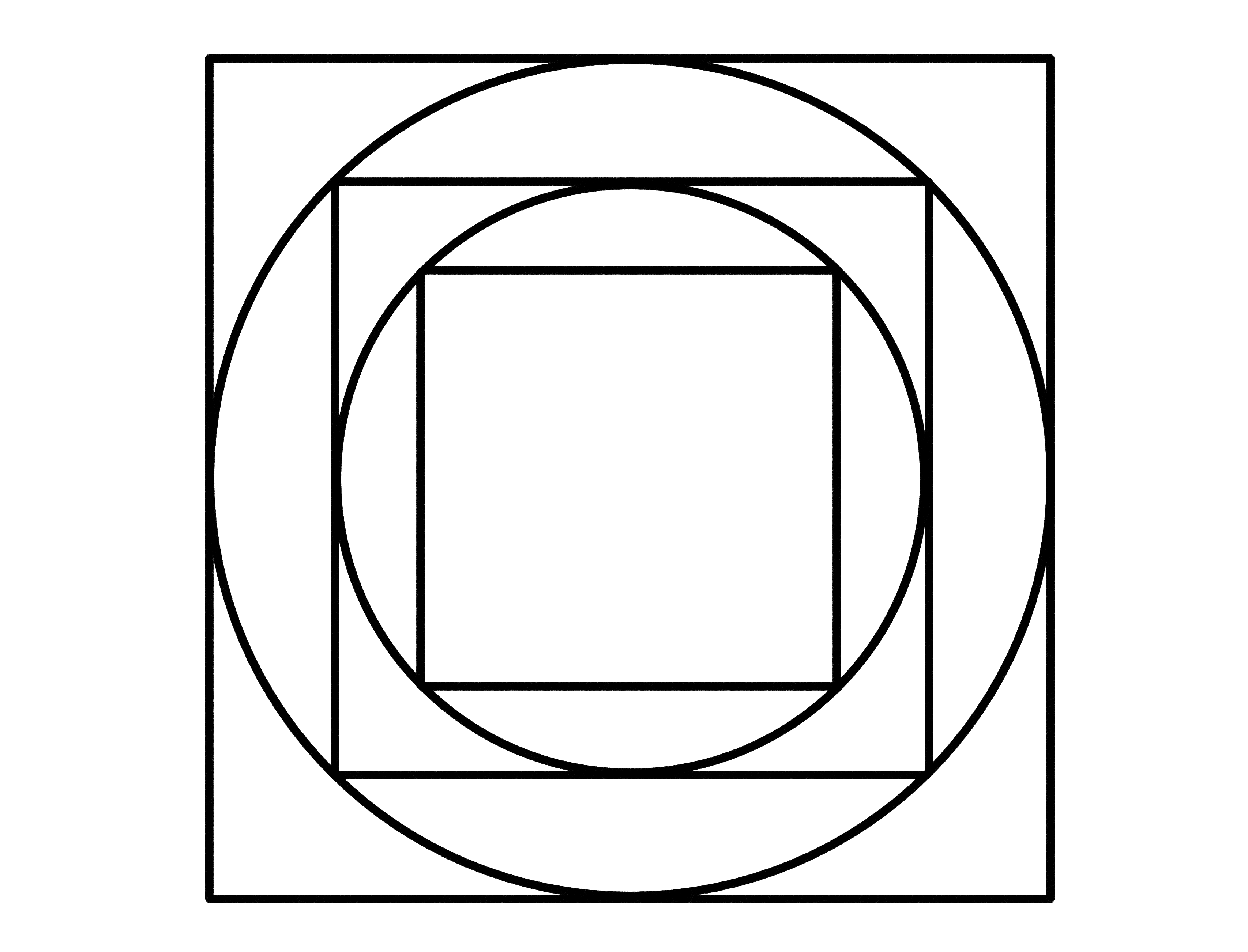
Klicken Sie die richtige Antwort an.

Aufgabe 7

Eine $100g$ schwere Kartoffel bestehe aus $99\%$ Wasser und $1\%$ Feststoffen. Nachdem sie eine Weile herumliegt, ist ihr Wassergehalt durch Verdunstung auf $98\%$ gesunken. Wie schwer ist sie jetzt?

Klicken Sie die richtige Antwort an.

Aufgabe 8

Bei welchen dieser Größenvergleichsaufgaben gibt es mehr als eine Strategie, um zum Ziel zu gelangen?

Es können eine oder mehrere Antwortmöglichkeiten richtig sein. Klicken Sie diese an.