Addition

(Padberg, 2017)

Wenn die grundlegenden Vorstellungen von Brüchen und Bruchzahlen gefestigt wurden, ist die Einführung von Addition und Multiplikation als geometrische Operationen relativ einfach. Auch hier liegt der Fokus auf diesen Darstellungen und nicht auf den abstrakten Formeln.

Brüche mit gleichem Nenner zu addieren, fällt den meisten Lernenden nicht schwer – insbesondere wenn die Analogie von Nennern bzw. Stammbrüchen als Einheiten eingeführt wurde.

Brüche mit unterschiedlichem Nenner auf denselben Nenner zu bringen, kann ebenso über Einheiten verdeutlicht werden. Sind zwei Strecken mit Längen $2\,\text{m}$ und $120\,\text{cm}$ gegeben, so können diese natürlich aneinander gehängt werden, um ihre Summe zu bestimmen. Aber die Addition der Zahlwerte ist nicht ohne Weiteres möglich. Sie müssen in die kleinere von beiden Einheiten umgewandelt werden, hier Zentimeter:

\[2\,\text{m} + 120\,\text{cm}\enspace =\enspace 200\,\text{cm} + 120\,\text{m}\enspace =\enspace 320\,\text{cm}\]

Das Ergebnis kann nicht immer in die größere von beiden Einheiten umgewandelt werden – zumindest nicht ohne die Einführung von Dezimalbrüchen. Die Übertragung auf Brüche erfolgt eins-zu-eins: Der Nenner gibt die Größe eines (Pizza-, Schokoladen-)Stücks an. Sind diese unterschiedlich, so müssen die Stücke weiter zerteilt werden:

\[\frac{2}{7} + \frac{5}{14}\enspace=\enspace \frac{4}{14} + \frac{5}{14}\enspace =\enspace \frac{11}{14}\]

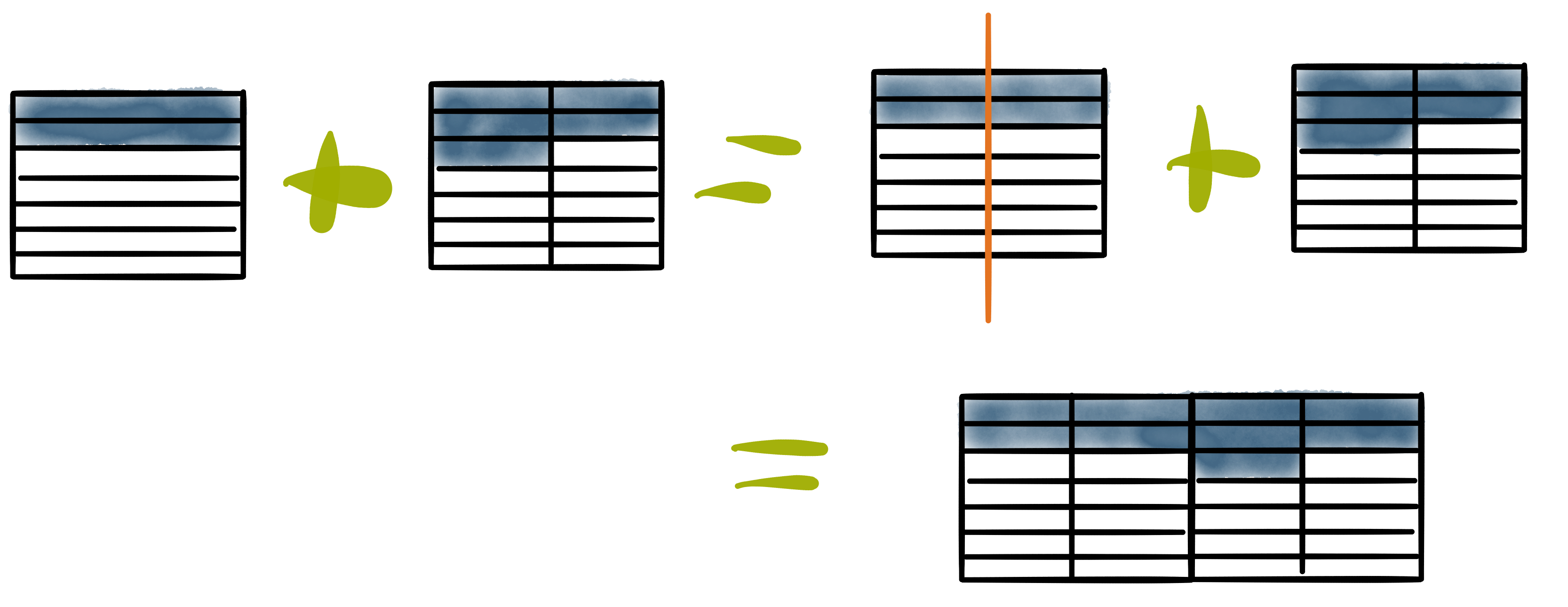
Ist wie hier ein Nenner ein Vielfaches des anderen Nenners, ist das besonders einfach. Ist das nicht der Fall, kann ein Vergleich mit SI-Einheiten nicht mehr herangezogen werden, da diese nur in Verhältnissen von Potenzen von 10 zueinanderstehen. Durch das Kombinieren mit imperialen Einheiten wie z.B. dem Zoll gelingt es aber:

\[2\,\text{in} + 3\,\text{cm} = 2\cdot 254\,\text{mm} + 3\cdot 10\,\text{mm} = 538\,\text{mm}\]

Es müssen also beide Einheiten so weit verfeinert werden, bis eine gemeinsame Einheit hervortritt. Das bedeutet aber, dass das Ergebnis hier weder in der einen noch der anderen Ausgangseinheit dargestellt werden kann; was so auch bei Brüchen auftritt:

\[\frac{1}{6} + \frac{5}{8} = \frac{4}{24} + \frac{15}{24} = \frac{19}{24}\]

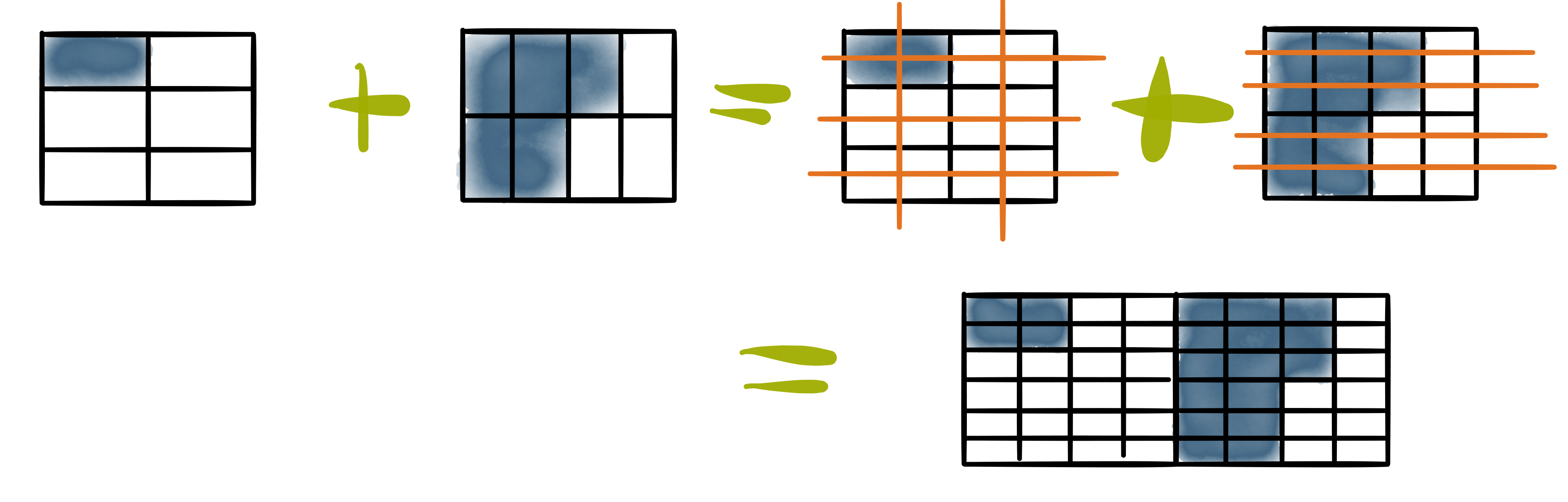
Der häufigste Fehler, der hier bei Lernenden auftritt, ist das Addieren von Zählern mit Zählern und Nennern mit Nennern (Padberg, 2017). Das hat seinen Platz in der Mathematik – wie im Ausblick besprochen wird – allerdings ergibt es für das Addieren von Zahlen als Größenmaß keinen Sinn. In der geometrischen Interpretation, der hier gefolgt wurde, ist das aber auch einleuchtend. Der Nenner eines Bruchs beschreibt die Größe von Stücken und der Zähler die Anzahl dieser Stücke. Die Gestalt der allgemeingültigen Formel zur Addition von Brüchen,

\[\frac{a}{b} + \frac{c}{d}\enspace =\enspace\frac{ad + bc}{bd},\]

ist somit nur eine Konsequenz der geometrischen Sichtweise und nicht inhärent richtig.

Ein weiterer, noch relativ häufiger Fehler tritt auf, wenn Brüche mit ganzen Zahlen addiert werden sollen (Padberg, 2017). Die ganze Zahl wird einfach zum Zähler hinzuaddiert: $\frac{a}{b} + n = \frac{a + n}{b}$. Da sowohl ganze Zahlen als auch Zähler von Brüchen die Anzahl von etwas beschreiben, ist dieser Fehler vielleicht sogar verständlicher als der vorhergehende. Allerdings hilft auch hier die geometrische Interpretation bei der Erklärung dieses Fehlers: Eine ganze Pizza plus eine halbe Pizza kann nicht zwei Hälften ergeben.

Die Subtraktion kann an dieser Stelle genauso eingeführt werden, wie die Subtraktion natürlicher Zahlen beziehungsweise wie die Einführung negativer Zahlen. Wie anfangs erläutert, werden negative Zahlen – natürlich oder gebrochen – in diesem Modul nicht näher besprochen.