Beweiskompetenz und Beweisbedürftigkeit
(Brunner, 2014; Winter, 1983)
Was ist die Beweiskompetenz?
Zur Beweiskompetenz gehören nach Brunner (2014, S. 79 ff.) sowohl eine kognitive Komponente als auch motivationale und emotionale Aspekte.

Was ist die Beweisbedürftigkeit?
Ziel des Lehrenden ist es, den Inhalt so auf- und vorzubereiten, dass die Lernenden eigenständig Interesse an dem Inhalt und Motivation zur Lösung der Beweis-/Argumentationsaufgaben entwickeln können. Dafür steht zu Beginn des Beweisprozesses eine nicht weiter begründete Behauptung, die einen spezifischen kognitiven Konflikt auslöst. Dieser wiederum resultiert in dem Bedürfnis, nach Gewissheit zu suchen. Die Lernenden werden idealerweise versuchen, in einem Prozess des Suchens, Überprüfens und Begründens diese Gewissheit zu erlangen.
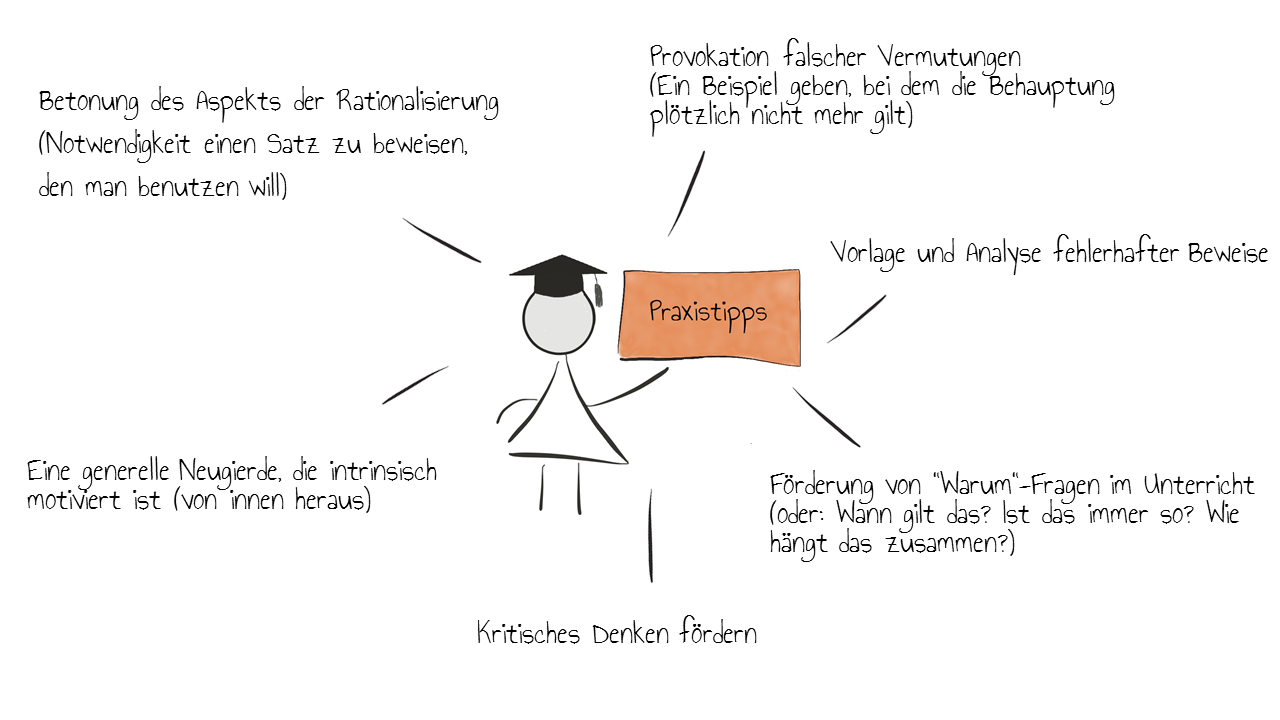
Wie kann die Beweisbedürftigkeit gefördert werden?
Ist eine Beweisbedürftigkeit bei den Lernenden vorhanden, so bildet sie eine gute Basis für einen Beweis. Beim Einsatz von Beweisen und Argumentationen im Unterricht ist es zielführend, wenn die Beweisbedürftigkeit der Lernenden geweckt wird. Dafür muss der Lehrende aktiv Zweifel an der Richtigkeit von Aussagen sähen. Dies geschieht am besten durch viele Warum-Fragen. Wie kann der Lehrende im Unterricht die Beweisbedürftigkeit sonst noch ausbilden?
Beispiele
- Zum Einstieg behaupten die Lehrenden, dass der Satz des Pythagoras immer für drei aufeinanderfolgende Zahlen gilt. Die Lehrenden könnten zwei, drei Beispiele aus den pythagoreischen Zahlentripeln zeigen, um dann mit einem Gegenbeispiel Beweisbedürftigkeit zu generieren.
- Auch die Umkehrung lädt zu kritischen „Warum“-Fragen ein. Warum ist jedes Dreieck rechtwinklig, bei dem sich die Seitenlängen durch den Pythagorassatz bestimmen lassen? Feststellen kann man dies, indem man die Klasse Dreiecke zu gegebenen Seitenlängen zeichnen lässt und plötzlich diesen Zusammenhang vermutet.
- Nach dem erfolgten Beweis des Satz des Pythagoras bietet es sich an, ihn ebenfalls auf ähnliche Figuren anzuwenden. Da die Lernenden nun einen vollständigen Beweis haben, an dem sie sich orientieren können, empfiehlt sich an dieser Stelle eine Partner- oder Kleingruppenarbeit. Durch kooperatives Lernen können Lernende zusammen beweisen, dass die unterschiedlichen Figuren tatsächlich den gleichen Flächeninhalt haben.