Der Vier-Farben-Satz
(Chartrand, Lesniak & Zhang 2010; Gonthier, 2008; MacKenzie, 2004; Maddison, 1897; Robertson, Sanders, Seymour & Thomas, 1996; Soifer, 2009; Wilson, 2013)
Wie im Verlauf des Moduls bereits erwähnt, werden Graphen für die unterschiedlichsten Probleme verwendet und verlangen dementsprechend nach verschiedenen Eigenschaften. Eine sehr starke solche Eigenschaft ist die Planarität.
Ein Graph heißt planar, wenn er so in die (Euklidische) Ebene gezeichnet werden kann, dass sich keine Kanten schneiden. Das Entscheidende hierbei ist, dass nur eine einzige solche Einbettung in die Ebene existieren muss. Insbesondere bedeutet das, dass ein Graph nur dann nicht planar ist, wenn sich in jeder möglichen Zeichnung mindestens zwei Kanten schneiden.
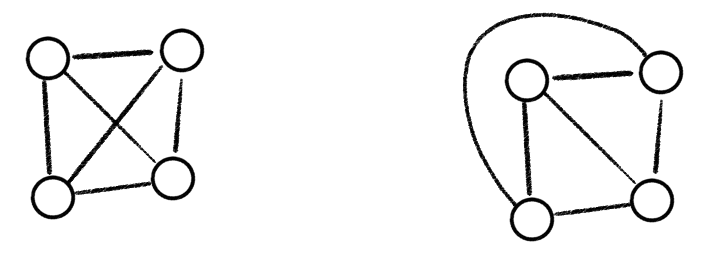
Im Bild oben ist ein und derselbe Graph auf zwei unterschiedliche Arten in die Ebene gezeichnet. Die linke enthält zwei sich schneidende Kanten und sagt deswegen nichts über die Planarität aus. Die rechte verbiegt eine der Kanten und erlaubt somit eine passende Einbettung. Der Graph ist also tatsächlich planar.
Ein nicht-planar Graph ist hier zu sehen:
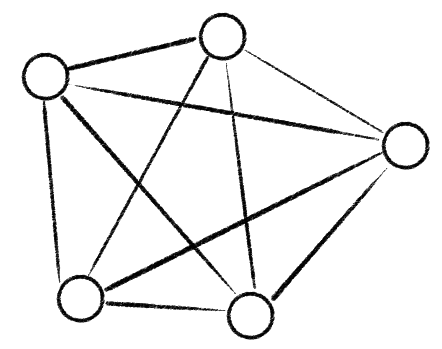
Wie bereits erwähnt, ist es im Allgemeinen sehr aufwendig zu zeigen, dass ein Graph planar ist. Der hier zu sehende ist allerdings vollständig: Jeder Knoten ist mit jedem anderen verbunden. Damit gibt es nur relativ wenig qualitativ unterschiedliche Konfigurationen, wie dieser Graph in die Ebene gezeichnet werden kann:
- Ob die Knoten ein konvexes Fünfeck bilden.
- Ob vier der Knoten ein konvexes Viereck bilden mit dem fünften Punkt im Inneren.
- Ob drei der Knoten ein Dreieck bilden mit den anderen beiden Knoten im Inneren.
Diese Fälle können explorativ in folgender dynamisch-interaktiver Visualisierung betrachtet werden. Sie erlaubt nur gerade Kanten zwischen den Knoten bestehen und vermittlet Nicht-Planarität deswegen nur qualitativ.Um die Nicht-Planarität dieses Graphen rigoros zu beweisen wird noch der Satz von Wagner und Fáry benötigt. Dieser besagt, dass wenn ein Graph planar ist, es auch immer eine Einbettung in die Zeichenebene gibt, bei der die Kanten Geraden bilden.
Anleitung: Die Knoten verschieben.
Die Bedingungen, unter denen ein allgemeiner Graph planar ist, werden im Satz von Kuratowksi beschrieben. Aber anstatt dieser allgemeinen Frage nachzugehen, wird hier nun eine konkrete Anwendung vorgestellt.
Der Vier-Farben-Satz
Wird eine Landkarte eingefärbt, so ist es meist aus ästhetischen Gründen erwünscht, dass keine zwei benachbarten Länder dieselbe Farbe haben. Hierbei stellt sich das praktische Problem, wie viele Farben mindestens notwendig sind, um eine Landkarte wie angegeben einzufärben.
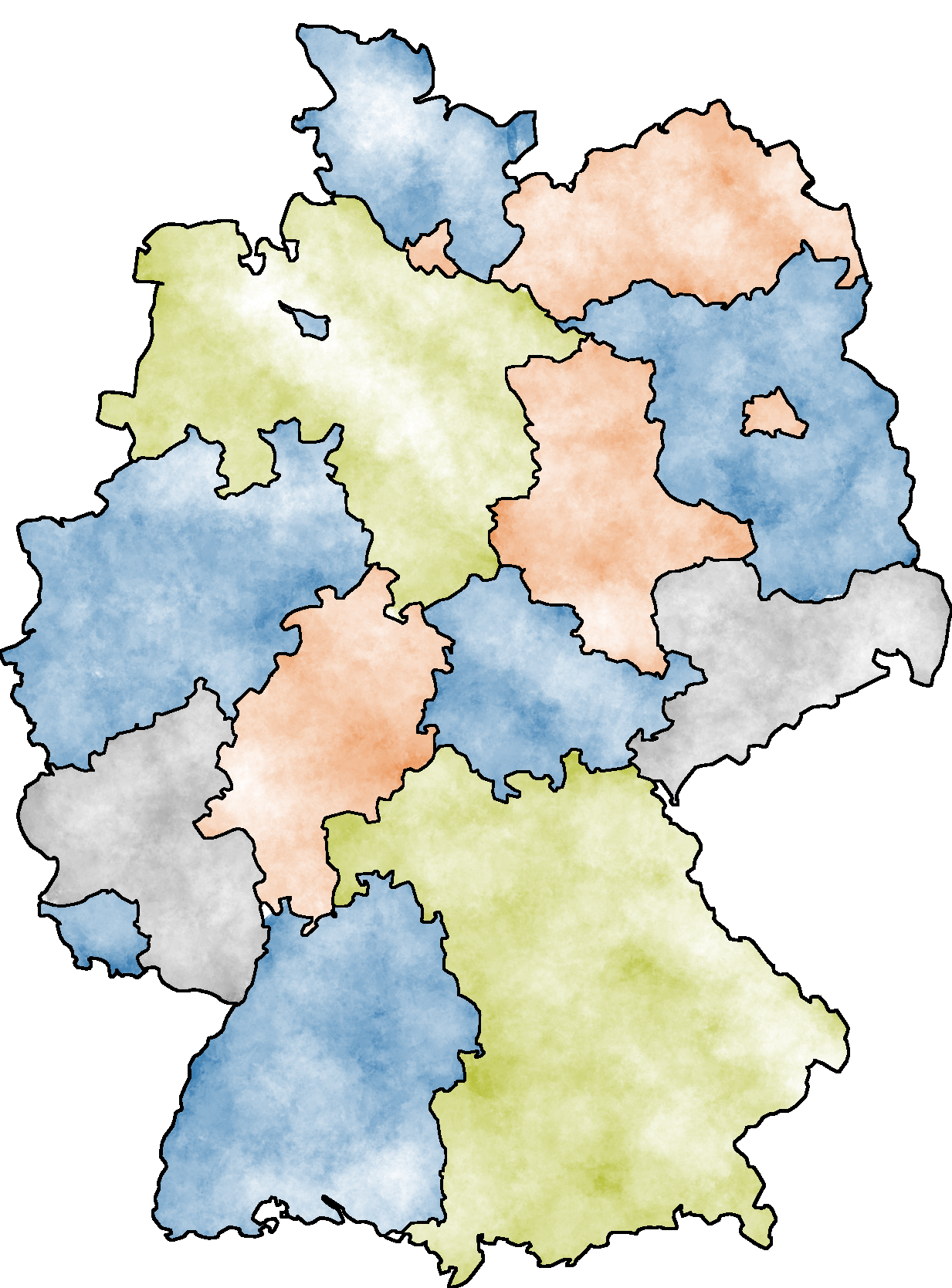
Um das Ganze graphentheoretisch zu formulieren, wird zuerst aus einer Landkarte ein Graph gebildet, der die relevanten Zusammenhänge sinnvoll modelliert. Hierzu wird als Beispiel eine Deutschlandkarte benutzt, die in die 16 Bundesländer unterteilt ist.
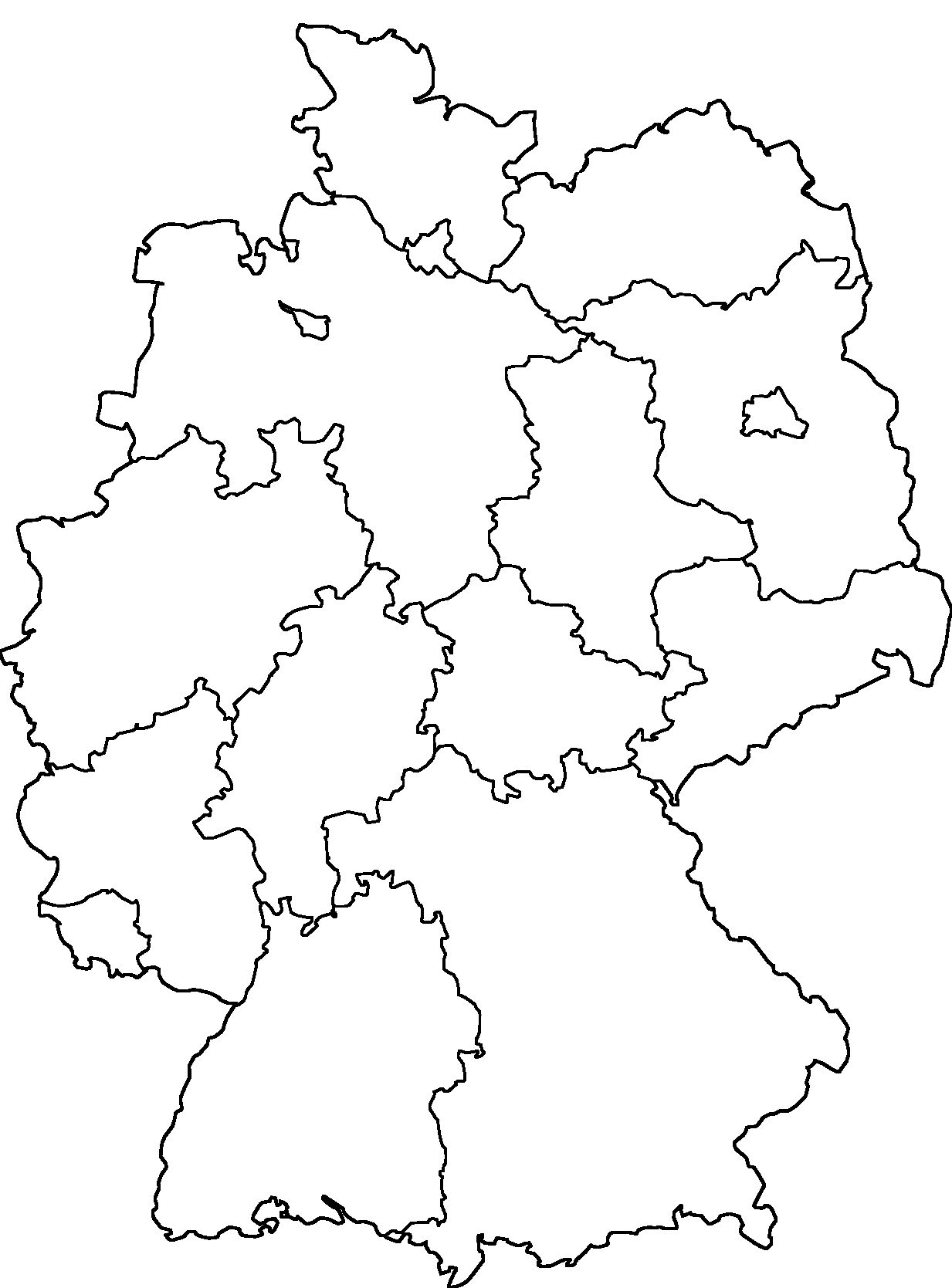
Die Länder selbst sind die Objekte und die Grenzen zwischen ihnen sind die Beziehungen, die zu betrachten sind. Es bietet sich also an, einen Graphen zu bilden, in dem die Knoten die Länder darstellen und die Kanten zwischen Knoten Grenzen zwischen Ländern. Wird ein Knoten pro Land in die Zeichnung hinzugefügt, ergibt sich:
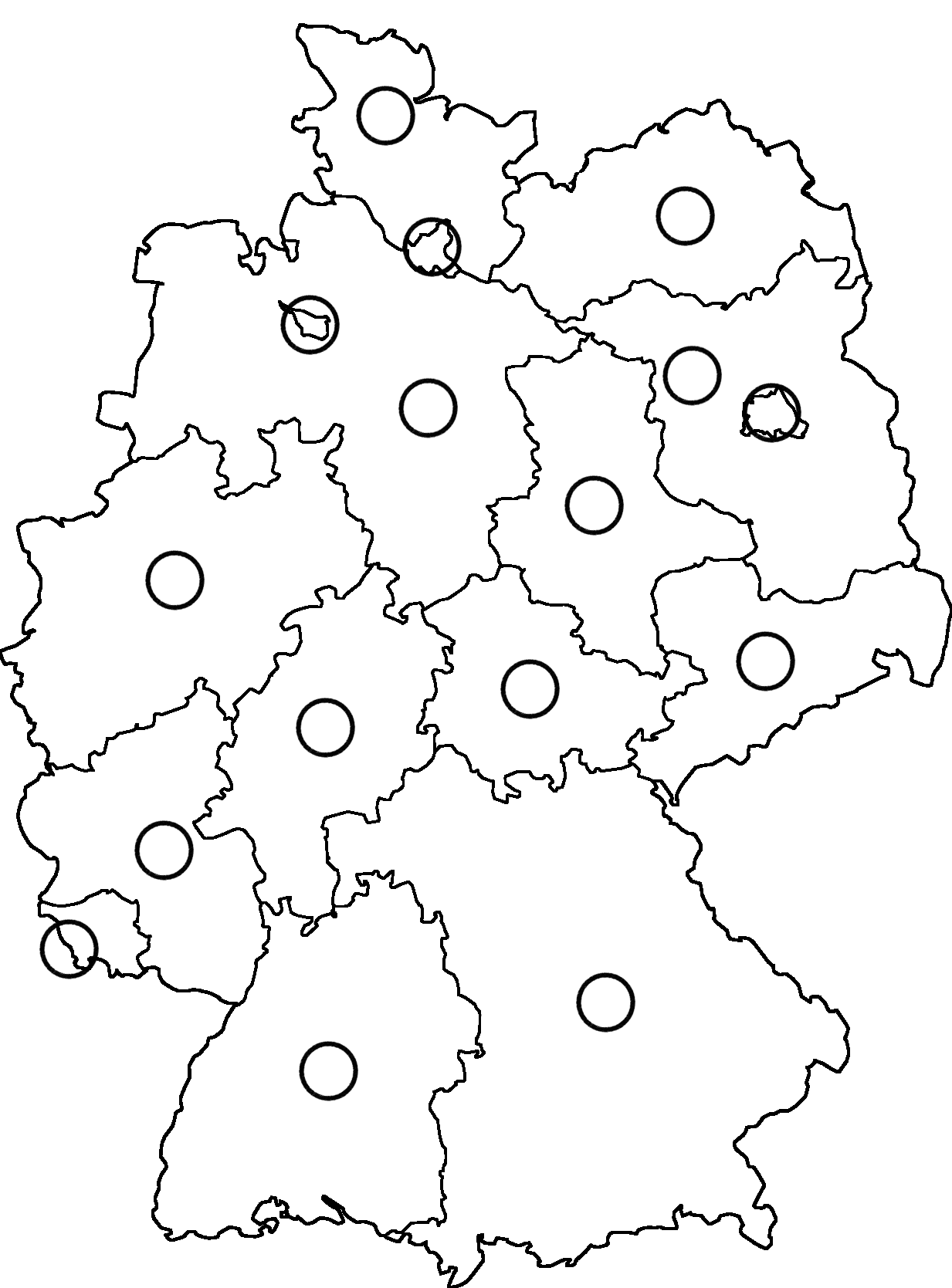
Um es optisch ansprechend und übersichtlich zu machen, sollten die Knoten genau in die Mitte der Bundesländer liegen. Allerdings ist das bei Niedersachsen und Brandenburg schwierig, da dort Bremen und Berlin mittig liegen. Anschließend wird genau dann eine Kante zwischen zwei Knoten eingezeichnet, wenn sich die zugehörigen Bundesländer berühren.
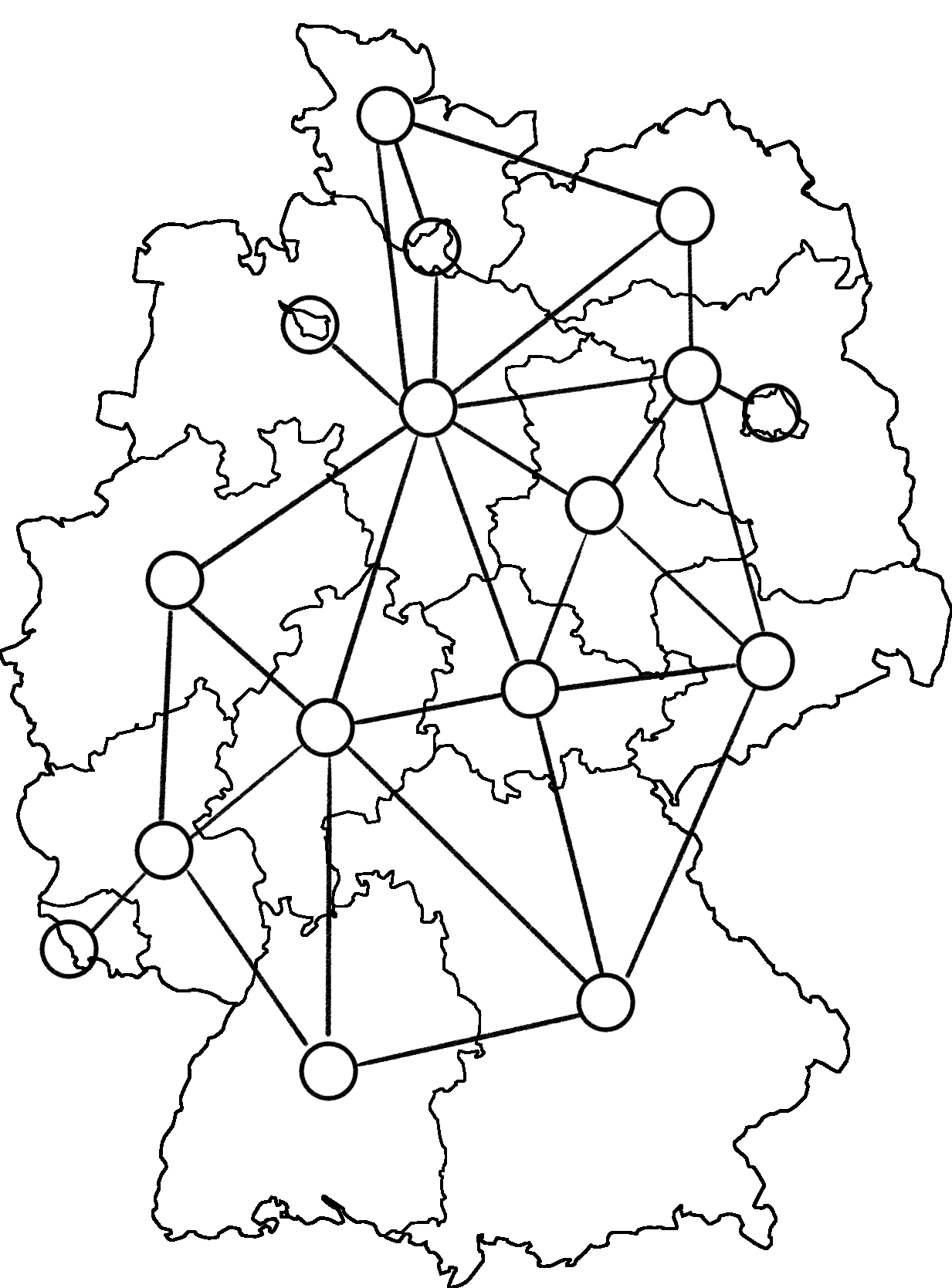
Der abstrakte Graph der deutschen Bundesländer, der somit entsteht, sieht folgendermaßen aus:
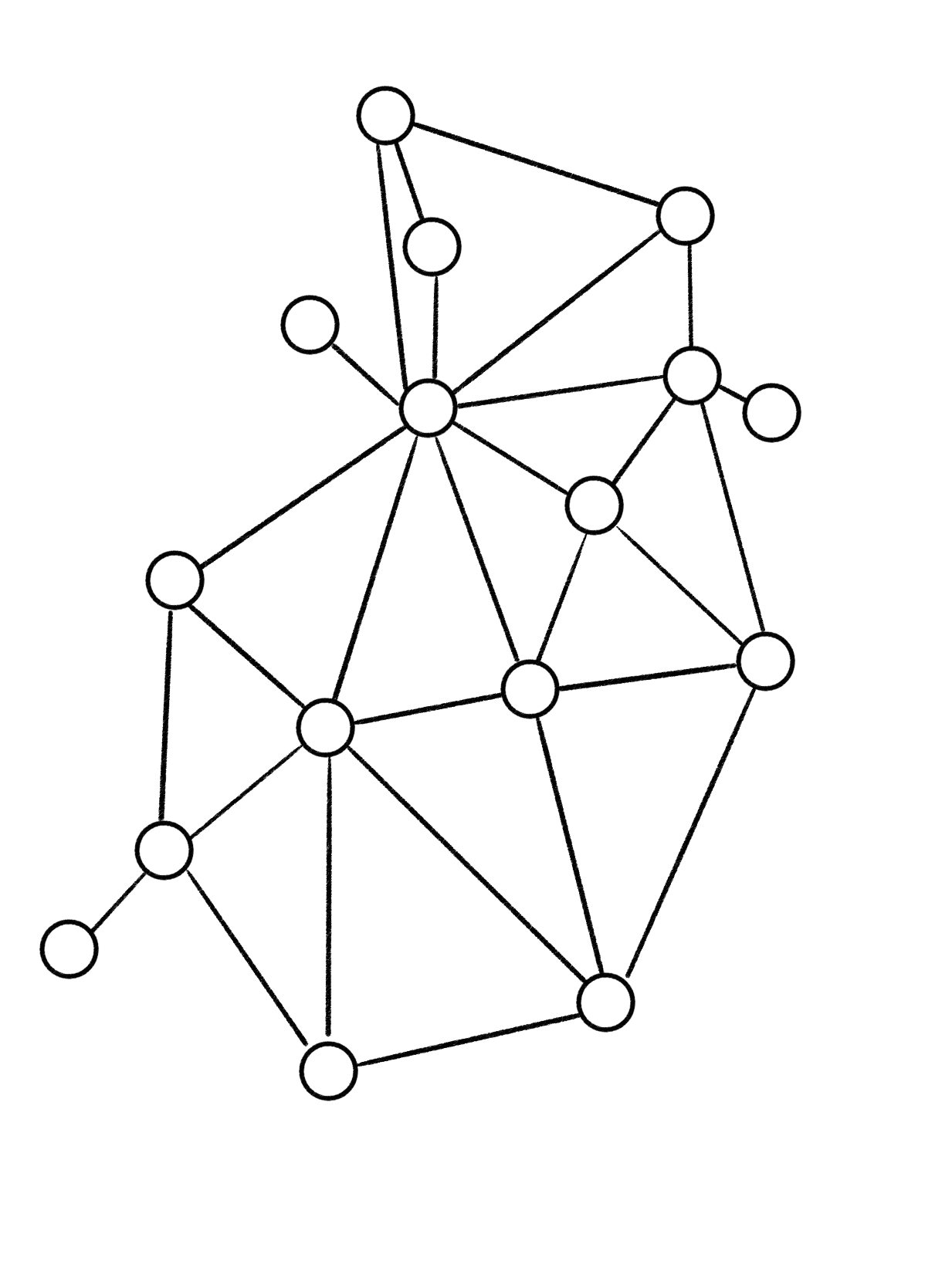
Das Färbarkeitsproblem lässt sich nun leicht für alle Graphen beschreiben, wenn wir daran denken, dass die Knoten Länder beschreiben:
Ein Graph heißt $k$-färbbar, wenn jedem Knoten eine von $k$ verschiedenen Farben so zugeordnet werden kann, dass keine zwei Knoten, die über eine Kante miteinander verbunden sind, dieselbe Farbe haben.
Trivialerweise ist ein Graph mit $n$ Knoten immer $n$-färbbar: Jedem Knoten kann eine andere Farbe zugeordnet werden. Die spannende Frage ist somit, was die kleinste Zahl an Farben ist, die gebraucht wird, um einen Graphen einzufärben. Je nachdem, welche Eigenschaften ein Graph hat, sieht die Antwort natürlich anders aus. Wir wollen uns nun auf Graphen beschränken, die, wie oben, Landkarten modellieren. Der Einfachheit halber beschränken wir uns auf Karten, bei denen die Landesgebiete zusammenhängend sind. (Gebiete wie etwa Alaska werden für diese Überlegungen dementsprechend ignoriert oder als eigenes Land betrachtet.) Solche Landkarten werden immer durch planare Graphen beschrieben: Würden sich im Graphen zwei Kanten schneiden, müssten sich die zugehörigen Grenzen auf der Landkarte schneiden, was nicht möglich ist. Nun ergibt es sich, dass sich die Frage nach der Färbbarkeit für alle planaren Graphen gleichzeitig beantworten lässt.
Satz: Jeder planare Graph ist $4$-färbbar. Sprich, jede Landkarte aus zusammenhängenden Staatsgebieten lässt sich immer mit maximal vier Farben so einfärben, dass keine zwei benachbarte Länder dieselbe Farbe haben.
Ein formaler Beweis dieses Satzes ließ sehr lange auf sich warten. Francis Guthrie beschrieb den Satz Mitte des 19. Jahrhunderts als Vermutung (Maddison, 1897; MacKenzie, 2004). Nachdem sich mehrere hundert Mathematiker an einer formalen Begründung versucht hatten, entstanden in der zweiten Hälfte des 20. Jahrhunderts mehrere Beweise derselben Art: Das Problem wurde auf mehrere Spezialfälle reduziert und diese wurden anschließend von einem Computerprogramm individuell überprüft. Der erste dieser Beweise von Heinrich Heesch in den 1960ern war noch theoretischer Natur und konnte wegen mangelnder Prozessorleistung der damaligen Computer nicht umgesetzt werden (Wilson, 2013). Der erste praktisch verwirklichte Beweis stammt von Appel und Haken von 1989 und verwendete 1936 Spezialfälle (Chartrand, Lesniak & Zhang 2010; Wilson, 2013). Roberston, Sanders, Seymour und Thomas konnten 1996 einen Beweis liefern, der mit nur 633 Spezialfällen auskam (Robertson, Sanders, Seymour & Thomas, 1996). Allerdings stießen diese Beweise bei vielen Mathematikern auf Kritik, da sie die Aussage nicht rein logisch erschlossen, sondern auf die Überprüfung einer großen Anzahl an Spezialfällen angewiesen waren, die zu alledem auch noch wegen ihrer Komplexität und Anzahl von einem Computer untersucht werden mussten. Georges Gonthier gelang es 2005 einen formalen Beweis für diese Aussage zu liefern, welcher nicht auf die Reduktion auf Spezialfälle angewiesen ist. Allerdings verwendete Gonthier ein Computerprogramm, um diesen Beweis zu erzeugen bzw. zu überprüfen (Gonthier, 2008).
Jedwede Art von Beweis, die bisher existiert, sprengt den Rahmen dieses Ausblicks. Und auch schon der Beweis für die schwächere Aussage, dass jeder planare Graph mit fünf Farben einfärbbar ist (was schon im 19. Jahrhundert gezeigt wurde (Soifer, 2009)) beansprucht mehrere Stunden einer Diskreten-Mathematik-Vorlesung. Allerdings stellt der Vier-Farben-Satz eine schöne Modellierungsaufgabe für den Schulunterricht dar und kann anhand diverser Landkarten explorativ verstanden werden. Es gibt zudem noch weitere Anwendungsmöglichkeiten dieses Satzes: Wie etwa, dass Funkmasten nur vier verschiedene Frequenzen benutzen müssen, damit zwei benachbarte Masten, deren Sendegebiete sich überlappen, sich nicht gegenseitig stören. Wenn die Masten allerdings ungeeignet platziert sind, ist der zugehörige Überlappungsgraph nicht mehr planar. Der Vier-Farben-Satz ist in diesem Beispiel also nicht universell anwendbar.
Abschließend soll darauf hingewiesen sein, dass für einen zufälligen Graphen immer damit gerechnet werden muss, mindestens vier Farben zu brauchen. Es können zwar leicht einzelne spezielle Graphen bzw. Landkarten konstruiert werden, die mit weniger Farben auskommen. Allerdings ist die folgende (fiktive) Karte nur mit vier Farben färbbar:
Der zugehörige Graph ist genau der, der am Anfang dieser Seite zu sehen ist. Und da dieser zusammenhängend ist, berührt jedes Land jedes andere. Alle Länder müssen deswegen eine andere Farbe haben.